一种基于信息几何学的分布式雷达目标跟踪方法

本发明属于雷达跟踪滤波领域，尤其涉及一种基于信息几何学的分布式雷达目标跟踪方法。

背景技术：

1、在分布式多传感器目标跟踪系统中，每个传感器具有独立的信息处理系统，能够独立对周围环境的目标进行跟踪，生成相应的目标航迹。分布式多传感器目标跟踪，也称为分布式多传感器数据融合。在这个系统中，各局部传感器首先基于单传感器多目标跟踪算法形成目标航迹，然后这些航迹被送入融合中心进行时空配准和航迹关联。最终，融合中心基于某种融合准则对来自同一目标的航迹进行估计融合，形成稳定、高精度的全局航迹。

2、多雷达数据融合是实现分布式雷达协同感知，实现信息互补、提高目标跟踪精度、提高轨迹检测概率的关键技术。分布式融合具有较高的生存性和稳定性，对数据传输的信道带宽要求低，对融合中心的计算能力要求低。分布式多传感器目标跟踪的具体过程主要包括目标跟踪、传感器配准、航迹关联和数据融合。最后也是最关键的阶段是同质或异构传感器数据的融合和利用。

3、基于分布式的目标跟踪研究现状比较丰富，包括卡尔曼滤波和粒子滤波算法、分布式领导节点和机器学习算法等。经典的分布式航迹估计融合算法包括简单凸组合融合算法、bar-shalomcampo融合算法、最大后验概率状态估计融合等。简单凸组合融合算法是传感器局部估计误差不相关条件的最优融合估计，它的融合结果与中心式融合相同，但是一般情况下很难获取数据的相关信息，为了解决这一问题，uhlmann提出了协方差交叉(covariance intersection,ci)融合算法。然而ci融合受限于高斯输入，跟踪精度并不是很高，信息几何为估计融合提供了强大的视角和更好的途径，比现有的方法更准确和全面。限制这些研究的一个主要问题可能是缺乏常用统计流形上测地线距离的明确表达式。因此，建立一种复杂的多模态运动模型，可以模拟更为真实的目标跟踪场景，在复杂场景下提出一种基于信息几何学的多雷达目标跟踪数据分布式融合算法，具有重要的研究意义和应用价值。

技术实现思路

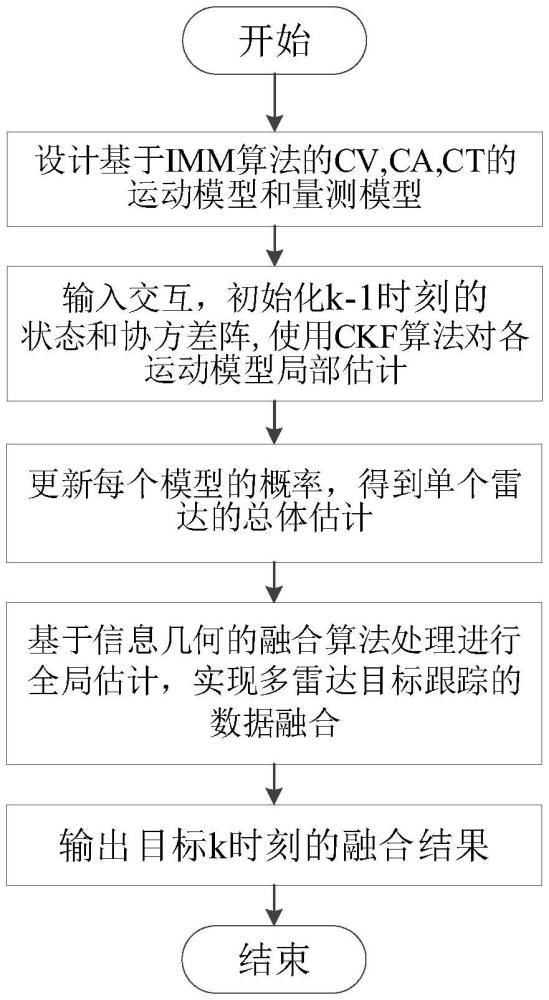
1、发明目的，本发明提出了一种基于信息几何学的多雷达目标跟踪数据分布式融合算法。通过融合来自多部雷达的信息来提高目标跟踪的精度和稳定性。该方法包括如下步骤：对于不同雷达估计误差之间的相关性问题，采用了一种基于容积卡尔曼滤波(cubaturekalman filter，ckf)算法的交互式多模型(interactive multi-model，imm)滤波方法来完成单个雷达传感器目标跟踪的局部估计；在高斯假设下提出一种测地投影(geodesicprojection，gp)融合算法，将目标跟踪的分布式数据融合问题转换到信息几何的框架下，完成局部估计后的全局融合。本发明保证了分布式传感器中的数据融合估计方法的有效性，并利用仿真验证了算法性能。

2、技术方案，为了实现上述发明目的，本发明提出一种基于信息几何学的分布式雷达目标跟踪方法，该方法包括如下步骤：

3、步骤一、基于交互式多模型imm算法建立目标运动模型和量测模型，初始化k-1时刻的每个运动模型的最优状态和协方差矩阵；

4、步骤二、基于初始化得到的各模型目标的状态估计和协方差矩阵，采用容积卡尔曼滤波ckf算法进行预测和更新，得到各运动模型更新后的目标状态，卡尔曼增益和协方差矩阵；

5、步骤三、根据容积卡尔曼滤波之后更新的结果，计算各个运动模型的似然函数，更新置信度，输出交互后的单个雷达的状态估计和协方差；

6、步骤四、将数据融合问题放置在信息几何的框架中，基于信息几何的测地线投影gp融合算法处理单个雷达局部估计值之间未知的相关性，对数据融合后的分布式雷达目标进行跟踪。

7、进一步的，步骤1)的具体方法如下：

8、步骤1.1)假设目标处于一个二维区域内，运动目标和观测站在同一平面上，设时间k非负，t为连续两次雷达测量的时间间隔，用(xk yk)，和表示k时刻笛卡尔坐标下目标的位置，速度和加速度，ω表示角速度，fcv，fca和fct分别表示匀速cv，匀加速ca和匀速转弯ct三个运动模型的目标状态的转移矩阵，gcv，gca和gct分别表示cv，ca和ct的过程噪声分布矩阵，ωk表示零均值高斯白噪声；

9、步骤1.2)cv目标状态变量表示为：ca目标状态变量表示为ct目标状态变量表示为：cv的状态方程表示为：xk+1(cv)＝fcvxk(cv)+gcvωk，ca的状态方程表示为xk+1(ca)＝fcaxk(ca)+gcaωk，ct的状态方程表示为：xk+1(ct)＝fctxk(ct)+gctωk，三个运动模型对应的目标量测方程表示为：

10、zk＝h(xk)+vk

11、式中，zk＝[rk θk]，rk和θk分别表示目标的测量距离和方向，量测噪声和分别表示距离和方位的测量误差，雷达测量方差σr，σα分别为距离和角度的测量标准差，h(xk)表示测量矩阵；

12、步骤1.3)假设有m种目标运动状态，目标以先验概率pij从运动模型i转移到运动模型j，i，j∈{1，...，m}，在k-1时刻，imm对目标状态协方差矩阵模型概率μi(k-1)和状态转移矩阵的值进行初始化设置，k+1时刻第i个模型状态表示为：xi(k+1)＝fi(k)xi(k)+gi(k)ωi(k)，式中，fi(k)表示目标状态的转移矩阵，gi(k)表示过程噪声分布矩阵，ωi(k)零均值高斯白噪声序列，xi(k)是k时刻第i个模型的模型状态。

13、进一步的，步骤2)的具体方法如下：

14、将前一时刻imm交互后得到的各模型目标的状态估计和协方差矩阵p0j(k-1)进行预测和更新，估计得到k时刻的卡尔曼增益kk，目标状态和协方差矩阵为pk|k。

15、进一步的，步骤3)的具体方法如下：

16、步骤3.1)更新每个运动模型的概率，用每个模型的似然函数λj(k)更新运动模型j的置信度式中，表示归一化常数，是模型j的归一化常数；

17、步骤3.2)将各运动模型融合后更新，输出交互后的单个雷达的状态估计和协方差

18、

19、式中，和pj(k)分别是是模型j的状态估计和协方差矩阵。

20、进一步的，步骤4)的具体方法如下：

21、步骤4.1)高斯假设条件下，将分布式数据融合问题放置在信息几何的框架中，在统计流形上，具有均值μ和协方差矩阵ω的高斯密度函数表示为n(μ，ω)，如果指定变量x，可以表示为n(x；μ，ω)，由均值向量μ和协方差矩阵ω参数化的m变量高斯或正态分布的流形可以表示为：

22、

23、其中，是m维实数向量的集合，是m×m实数对称正定矩阵的集合；

24、步骤4.2)对于有r个雷达的分布式系统，第i个局部估计具有局部后验密度表示为pi，假设每个概率密度p(x；σ)是参数密度族s中的一个点，当s被视为配备fisher度量的黎曼流形时，产生与信息相关的测地线距离d(·，·)，则数据融合准则为：

25、

26、令局部后验概率密度函数均值协方差zi表示x的测量值；

27、步骤4.3)考虑上一步骤的数据融合准则，求解的最优解问题化简为：

28、

29、gp算法依次求解ω和μ，则等式约束改变为如下：

30、

31、从给定点pi＝n(μp，ωp)到子流形的测地线距离如下：

32、

33、pi在上的投影为n(μ，ω)，μp，ωp分别是pi点的均值和协方差，经过推导和化简得到：

34、

35、式中，

36、步骤4.4)令使用broyden-fletcher-goldfarb-shanno(bfgs)方法更新μ和梯度迭代后计算出均值的最优估计值和协方差矩阵p，融合算法处理单个雷达局部估计值之间未知的相关性，完成数据融合后的分布式雷达目标跟踪

37、有益效果：与现有技术相比，本发明的技术方案具有以下有益技术效果：

38、(1)本发明通过融合多个局部雷达的信息，显著提高了目标跟踪的精度和稳定性。提出的基于ckf的imm多模型滤波方法模拟更为真实的目标跟踪场景，有效地完成了分布式雷达传感器的局部估计。

39、(2)在高斯假设下，采用的gp融合算法将数据融合问题放置在信息几何的框架中，实现了更高效的分布式全局融合。解决了不同雷达估计误差之间的相关性问题。通过实际测量验证了算法的性能，确保了方法的实用性和有效性。