基于加速度计径向观测噪声确定卫星重力测量误差的方法

本发明属于卫星重力测量，更具体地，涉及一种基于加速度计径向观测噪声确定卫星重力测量误差的方法。

背景技术：

1、在重力卫星任务中，加速度计的作用是测量卫星受到的非保守力，但是由于加速度计本身的结构设计及在轨环境的影响等，其在轨观测数据(加速度计的观测值)不可避免地会混入各种噪声。加速度计作为重力卫星的核心载荷，其观测噪声与重力测量误差密切相关。清晰准确地把握加速度计的观测噪声(加速度计的观测值与真值之间的误差即为观测噪声，或观测误差)与重力测量误差之间的映射关系对于重力卫星载荷的精度指标设计、重力测量误差的传播机制等具有重要意义；其中，加速度计径向观测噪声对重力测量误差的影响最大。

2、现有技术中，有通过数值法研究加速度计观测误差与重力测量误差之间的映射关系，但是数值法无法得到普适性的规律，并且计算过程复杂、计算量大。还有通过半解析法研究加速度计观测误差与重力测量误差之间的映射关系，该方法在线性希尔方程的近似以及标称轨道近似下将星间距离用傅里叶级数表达，并建立了重力位系数和傅里叶系数之间的关系，这种方法与数值法相比，虽然一定程度上降低了计算量，但是仍然无法直接反映载荷误差(加速度计观测误差)和重力测量误差之间的关系，并且也使得在进行重力卫星载荷的精度指标设计时，仍然存在计算量较大的问题；并且，载荷误差到重力测量误差的传播机制依旧模糊不清。

技术实现思路

1、针对现有技术的以上缺陷或改进需求，本发明提供了一种基于加速度计径向观测噪声确定卫星重力测量误差的方法，其目的在于基于加速度计径向观测噪声快速确定其对卫星重力测量误差的贡献，提升计算效率，并明确加速度计观测噪声到重力测量误差之间的传播机制。

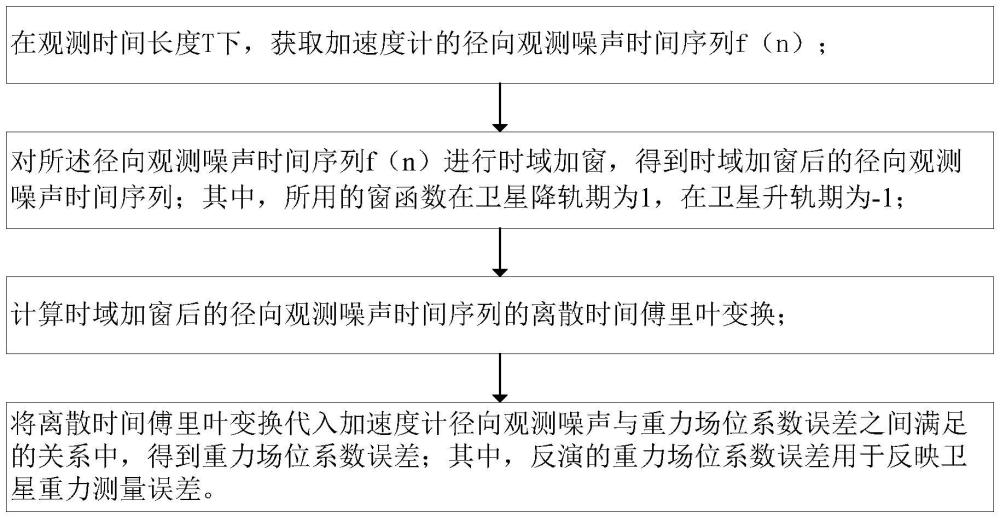
2、为实现上述目的，按照本发明的第一方面，提供了一种基于加速度计径向观测噪声确定卫星重力测量误差的方法，包括：

3、在观测时间长度t下，获取加速度计的径向观测噪声时间序列f(n)；

4、对所述径向观测噪声时间序列f(n)进行时域加窗，得到时域加窗后的径向观测噪声时间序列；其中，时域加窗所用的窗函数为w(n)，在卫星降轨期，所述窗函数w(n)＝1，在卫星升轨期，所述窗函数w(n)＝-1；

5、计算时域加窗后的径向观测噪声时间序列的离散时间傅里叶变换f；

6、将所述离散时间傅里叶变换f代入加速度计径向观测噪声与重力场位系数误差之间满足的关系中，得到重力场位系数误差δklm；其中，所述重力场位系数误差δklm用于反映卫星重力测量误差；

7、所述加速度计径向观测噪声与重力场位系数误差之间满足的关系为：

8、

9、式中，l、m为预设的重力场位系数的阶和次；glm(z)为基于缔合勒让德函数确定的傅里叶系数；ωθ为卫星飞行的角速度，ωλ为地球自转的角速度，g是引力常量，m是地球质量，r是地球平均半径，h是卫星轨道高度。

10、进一步地，确定所述加速度计径向观测噪声与重力场位系数误差之间满足的关系，包括：

11、建立重力场位系数误差δklm与加速度计径向观测噪声的空域分布δgz(θ，λ)之间满足的关系s1：

12、

13、其中，为ylm(θ，λ)的共轭，ylm(θ，λ)为重力位的复球函数ylm(θ，λ)；θ和λ分别表示卫星在球坐标下的纬度和经度；ω表示在球面积分的立体角；

14、将所述关系s1中的立体角积分∫δgz(θ，λ)·ylm(θ，λ)dω转换为二重积分

15、在卫星极圆轨道近似下，将卫星降轨或升轨的星下点轨迹投影到平面直角坐标系下，并将投影平面划分为k个平行四边形；将所述二重积分表示为在k个平行四边形内的定积分之和，进而得到卫星降轨或升轨过程中二重积分与加速度计径向观测噪声含时形式δgz(t)之间的关系；其中，δgz(t)在观测时间长度t下的离散形式为所述径向观测噪声时间序列f(n)；

16、联立卫星降轨和升轨过程中二重积分与加速度计径向观测噪声含时形式δgz(t)之间的关系，得到所述二重积分与加速度计径向观测噪声含时形式δgz(t)之间的关系s2；

17、将所述关系s2以及时域加窗后的径向观测噪声时间序列的离散时间傅里叶变换f代入所述关系s1中，得到所述加速度计径向观测噪声与重力场位系数误差之间满足的关系。

18、进一步地，卫星降轨过程中二重积分与加速度计径向观测噪声含时形式δgz(t)之间的关系为：

19、

20、其中，ti表示卫星降轨时在第i条星下点轨迹起始位置时的时刻，δt为从卫星从起始时刻开始飞过整条星下点轨迹所经历的时间；

21、卫星升轨过程中二重积分与加速度计径向观测噪声含时形式δgz(t)之间的关系为：

22、

23、其中，ti′表示卫星升轨时在第i条星下点轨迹起始位置时的时刻。

24、进一步地，所述关系s2为：

25、

26、其中，w(t)为所述窗函数w(n)的含时形式。

27、进一步地，所述傅里叶系数glm(z)通过如下公式确定：

28、

29、其中，plm(cosθ)为缔合勒让德函数，θ表示卫星在球坐标下的纬度；式中，flm(z)为缔合勒让德函数plm(cosθ)的三角展开系数；

30、flm(z)与glm(z)之间满足：

31、glm(z)＝flm(z-1)-flm(z+1)z∈[-l+1：2：l-1]

32、glm(-l-1)＝-flm(-l)

33、glm(l+1)＝flm(l)。

34、按照本发明的第二方面，提供了一种确定重力卫星载荷设计精度指标的方法，包括：

35、采用第一方面任一项所述的基于加速度计径向观测噪声确定卫星重力测量误差的方法得到重力场位系数误差δklm；

36、基于所述重力场位系数误差δklm与已知的重力测量需求之间满足的关系：求解加速度计径向观测噪声在不同频率处的值，以确定加速度计径向观测噪声的幅频特性和相频特性；

37、基于所述幅频特性和相频特性确定重力卫星载荷设计的精度指标。

38、按照本发明的第三方面，提供了一种电子设备，包括计算机可读存储介质和处理器；

39、所述计算机可读存储介质用于存储可执行指令；

40、所述处理器用于读取所述计算机可读存储介质中存储的可执行指令执行第一方面任一项所述的基于加速度计径向观测噪声确定卫星重力测量误差的方法，或/和，执行第二方面所述的确定重力卫星载荷设计精度指标的方法。

41、按照本发明的第四方面，提供了一种计算机可读存储介质，其上存储有计算机程序，所述程序被处理器执行时实现如第一方面任一项所述的基于加速度计径向观测噪声确定卫星重力测量误差的方法，或/和，执行时实现如第二方面所述的确定重力卫星载荷设计精度指标的方法。

42、按照本发明的第五方面，提供了一种计算机程序产品，当所述计算机程序产品在计算机上运行时，使得计算机执行第一方面中任意一项所述的基于加速度计径向观测噪声确定卫星重力测量误差的方法，或/和，执行如第二方面所述的确定重力卫星载荷设计精度指标的方法。

43、总体而言，通过本发明所构思的以上技术方案，能够取得以下有益效果：

44、(1)本发明的基于加速度计径向观测噪声确定卫星重力测量误差的方法，直接建立了不同阶和次下重力场位系数误差δklm与加速度计径向观测噪声频谱之间的关系，该关系直接反映载荷误差(加速度计径向观测误差)和重力测量误差之间的关系，基于该关系可快速确定加速度计径向观测噪声对卫星重力测量误差的贡献，提升了计算效率，并明确了加速度计观测噪声到重力测量误差之间的传播机制；并且，在基于重力场位系数误差δklm确定重力卫星载荷设计的精度指标时，也大幅降低了计算量。

45、(2)进一步地，本发明给出了加速度计径向观测噪声与重力场位系数误差之间满足的关系的一种建立方法，通过首先建立重力场位系数误差δklm与加速度计径向观测噪声的空域分布δgz(θ，λ)之间满足的关系s1，将关系1中的立体角积分转换为二重积分，并在卫星极圆轨道近似下，考虑到卫星降轨或升轨的星下点轨迹投影到平面内是一簇平行线，因此，将投影平面划分为若干个平行四边形，通过计算二重积分在多个平行四边形内的定积分之和，进而建立二重积分与加速度计径向观测噪声含时形式δgz(t)之间的关系s2，并将关系s2以及时域加窗后的径向观测噪声时间序列的离散时间傅里叶变换f代入关系s1中，即可得到不同阶和次下重力场位系数误差δklm与加速度计径向观测噪声频谱之间的关系，可以直观地分析加速度计频域噪声对于重力场位系数的影响机制。