一种多尺度沉积旋回相空间精细表征方法、系统及应用

本发明属于石油地球物理勘探，主要是用于辅助层序地层学研究的一种多尺度沉积旋回相空间精细表征方法、系统及应用。

背景技术：

1、层序地层学的基本论点是地层单元的几何形态及岩性受海平面升降、构造沉降、沉积物供给和气候四大因素控制(mclaughlin等，2005)。这些因素在不同尺度上发挥作用并呈现周期性变化，因此沉积层序也具有多尺度和周期性的特征。沉积旋回是沉积层序的基本构成单元，是不同尺度周期性沉积事件叠加的结果。区域或全球沉积事件影响不同尺度沉积序列的叠加模式。沉积旋回一般由一些基本单元组成，包括海侵旋回单元和海退旋回单元。对于海侵旋回，砂岩的厚度随着深度的增加而增加，而沉积物的粒度则由细变粗，这表明了海侵沉积序列。对于海退旋回，砂岩的厚度随着深度的增加而减小，沉积物的粒度则由粗变细，这表明了海退沉积序列(melani等，2020；rossi等，2020；zhang等，2017)。通常，一个大型层序由几个小规模旋回组成，记录了沉积环境中海侵和海退层序的证据(goldhammer等，1990；melani等，2020)。因此，对多尺度的沉积旋回进行精细表征与划分是后续沉积环境研究、层序地层学分析和储层预测的基础，也是建立构造和地层格架的重要步骤。

2、测井技术在井孔内对地下地层介质进行精细测量，是表征和划分多尺度沉积旋回最常见的地球物理工具(vermeer等，1992；coconi-morales等，2010)。然而，测井数据仅是一孔之见，其空间覆盖能力有限。相比之下，地震反射数据具有更好的空间覆盖能力，其携带了地下地层的岩性和物性信息，包含大量关于多尺度沉积旋回的信息(zeng，2013)。因此，有效地从地震数据中提取沉积旋回信息对沉积旋回的识别和解释具有重要意义。

3、数据驱动的分解方法已被用于从地震数据中提取沉积旋回信息。liu等人(2015)采用经验模态分解方法将地震信号分解为代表不同尺度沉积旋回的本征模态函数，以辅助多尺度沉积旋回的表征。然而，经验模态分解方法不能人为的确定本征模态函数的最佳个数。为了解决这一问题，li等人(2017)引入了一种基于变分模态分解的方法，该方法可人为的定义本征模态函数的个数。尽管这种方法提供了更多的灵活性，但对其结果的解释仍然高度主观且易受解释者经验的影响。因此，这些数据驱动的分解方法需要解决的一个关键问题是建立本征模态函数与不同尺度地质构造之间的确定性关系。此外，还需要更加合理的准则确定最佳本征模态函数的个数(tian等，2022)。

4、为了解决以往工作的局限性，申请人前期提出了一种增强的多通道变分模态分解方法，并提出了一种地震数据分解的工作流程，以辅助多尺度层序地层解释(tian等，2022)。该方法首先阐明了本征模态函数与不同尺度地质构造之间的关系。随后，提出了一种基于尺度空间表示和压缩映射算子的本征模态函数的个数的确定方法。最后，采用多通道变分模态分解方法分解地震数据，辅助不同尺度沉积层序边界的解释。然而，这些模态分解方法的分解结果，即不同尺度的地震反射波形，仍需由经验丰富的解释人员进行解释以推断沉积层序，从而阻碍了沉积旋回单元的直接划分。

5、时频分析方法可以直观地反映由于沉积旋回内薄层厚度变化导致的地震信号瞬时主频变化特征(tian等，2022)。因此，时频分析方法也是表征沉积旋回的最常用工具之一。准确表征由薄层厚度变化引起的主频变化特征是利用时频分析方法辅助沉积旋回划分的关键问题。该领域的开创性研究可以追溯到1980年，由俄罗斯勘探地球物理研究所提出的基于线性时频变换的沉积旋回划分方法(mushin等，2000)。

6、然而，线性时频分析方法的时频谱在时频平面上沿频率轴扩散(huang等，2016)，导致时频分辨率低，阻碍了沉积旋回的识别。为了解决这一缺陷，daubechies等人(2011)引入了同步挤压变换。同步挤压变换通过沿频率轴同步挤压时频谱以获得高分辨率的时频谱。尽管这种方法为沉积旋回分析提供了强大的工具，但时频原子的选择决定着所获得结果的可解释性。gao等人(2001)认为当基小波与地震子波非常相似时，连续小波变换的时频谱具有更强的噪声鲁棒性和可读性。为了更好地匹配地震子波，gao等人(2006)提出了一种名为三参数小波的基小波。通过调整其三个参数可使其波形与待分析地震数据的地震子波匹配。以匹配地震子波为准则，我们结合三参数小波和深度神经网络提出了一种最优基小波构造方法。该方法首先使用交替迭代深度神经网络估计地震子波，然后采用三参数小波拟合地震子波以获得最优基小波。尽管最优基小波变换实现了地震数据的高分辨率谱分解(tian等，2021)，但其频率分辨率低，这不利于沉积旋回的主频特性的表征工作。

7、为了解决上述限制，我们前期结合同步挤压变换与最优基小波，提出了一种同步挤压最优基本小波变换，以实现沉积旋回的最优表征。该方法通过定义同步挤压变换的主频定位条件和基小波与地震子波之间的相似系数条件来实现地震数据主频特征的最优表示，继而实现沉积旋回的最优表征(tian等，2022)。但该方法直接处理包含多尺度层序地层信息的地震数据，导致时频谱中不同尺度沉积旋回的信息相互叠加。采用这种同时包含多尺度沉积层序信息的时频谱将降低后续多尺度沉积旋回单元划分的准确性。

8、以上现有技术具有以下缺点：

9、(1)现有的基于模态分解方法对地震数据的分解结果，是包含不同尺度地质构造信息的不同尺度地震反射波形，其结果仍需由经验丰富的解释人员进行解释，以推断沉积规律，这将引入人为经验误差，不便于沉积旋回单元的直接划分。

10、(2)现有的基于同步挤压最优基小波变换的沉积旋回表征方法直接处理包含多尺度沉积层序信息的地震数据，导致时频谱中同时包含不同尺度沉积旋回信息。使用这种多尺度沉积旋回信息混合的时频谱，将降低后续多尺度沉积旋回单元划分的准确性。

技术实现思路

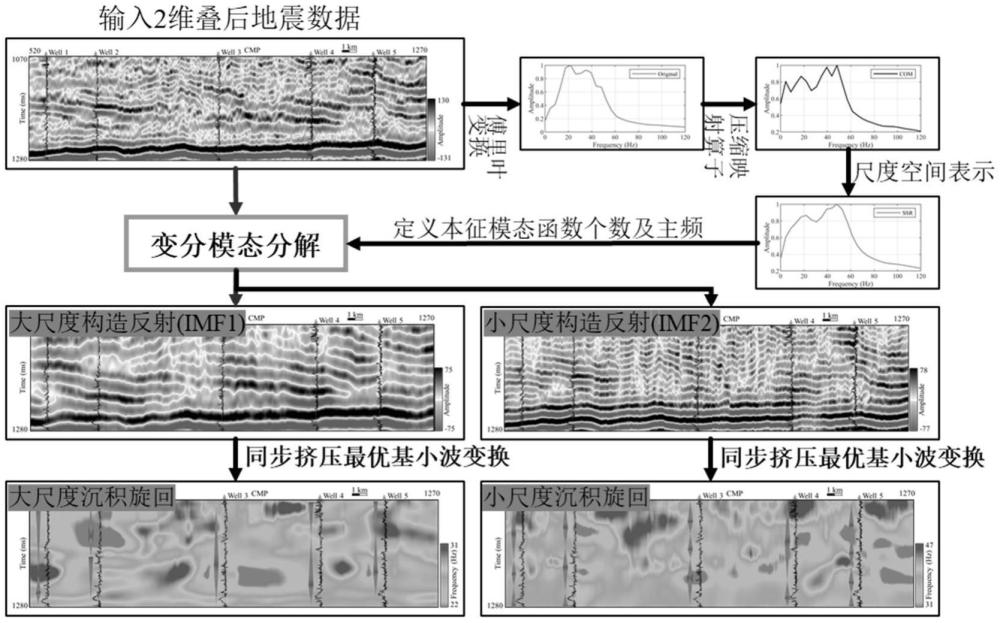
1、为了克服上述现有技术的缺点，本发明的目的在于提供一种多尺度沉积旋回相空间精细表征方法，该方法结合变分模态分解方法与同步挤压最优基小波变换，提出用于多尺度沉积旋回表征的工作流程。首先通过理论推导给出了不同尺度地质构造与本征模态函数之间的关系，并提出本征模态函数个数的确定方法。考虑到计算效率与分解结果的横向连续性问题，我们改进了变分模态分解算法，即根据平滑的反射系数振幅谱确定本征模态函数个数及其中心频率。在此基础上结合同步挤压最优基小波变换与脊提取方法提出了一种新的地震数据瞬时主频属性的提取方法，从而实现多尺度沉积旋回表征。

2、为了达到上述目的，本发明采用以下技术方案予以实现：一种多尺度沉积旋回相空间精细表征方法，包括以下步骤：

3、计算二维地震数据平均傅里叶振幅谱；

4、计算平均反射系数振幅谱；

5、采用尺度空间表示方法计算平滑的反射系数振幅谱，根据反射系数振幅谱与经验模态之间的关系，设置平滑反射系数谱的极值个数为本征模态函数分量的个数，极值频率为每个本征模态函数分量的中心频率；

6、采用变分模态分解方法对输入的二维地震数据进行分解，得到能够表征不同尺度地质构造的地震反射特征的本征模态函数分量；

7、采用同步挤压最优基小波变换分别计算每个二维本征模态函数分量的每个地震道，获得每个地震道的时频谱，

8、采用脊线提取方法从每个地震道的时频谱中提取瞬时主频曲线，获得二维瞬时主频属性剖面，

9、利用瞬时主频属性剖面解释沉积旋回单元横向展布规律，即多尺度沉积旋回相空间精细表征。

10、进一步的，计算平均反射系数振幅谱包括采用压缩映射算子从地震数据平均傅里叶振幅谱中提取地震子波振幅谱，使用地震数据平均傅里叶振幅谱除以地震子波振幅谱得到反射系数振幅谱

11、进一步的，采用压缩映射算子从地震数据振幅谱中提取地震子波振幅谱；

12、引入用于计算地震子波谱的压缩映射算子，设地震子波谱在所指定的频带内[fl,fh]表现为平滑且单峰的函数：

13、

14、q∈(0,1)，0≤fq(|w|；f)≤1，令cq＞0，α,β＞1，压缩映射算子p为

15、

16、设置迭代初始值为：

17、

18、通过压缩映射算法迭代|w|k＝p(|w|k-1)使其收敛至不动点|w|*，所述不动点对应被估计出来的地震子波谱(|w|*)1/q；

19、使用地震数据振幅谱|s(f)|除以地震子波振幅谱|w(f)|得到反射系数振幅谱|rk(f)|：

20、

21、这里ε≠0，防止|w(f)|＝0。

22、进一步的，根据反射系数谱与经验模态之间的关系，设置平滑反射系数谱的极值个数为本征模态函数分量的个数，极值频率为每个本征模态函数分量的中心频率包括：基于理论推导得到反射系数振幅谱与不同尺度地质构造之间的关系，如下式：

23、

24、将不同尺度结构的地震反射定义为经验模态函数，式(1)中|rk(f)|代表第k个尺度的地质构造对应的反射系数的振幅谱，ckj表示第k个经验模态函数中第j个采样点的反射系数值，(tkm-tkn)表示在第k个尺度下两个反射系数点m和n之间的时间差，定义绝对值较小的k表示大尺度构造，大值k表示小尺度构造，方程(1)表明，|rk(f)|的第一个极值点的频率与(tkm-tkn)成反比。

25、进一步的，采用变分模态分解方法对输入的二维地震数据进行分解，得到能够表征不同尺度地质构造的地震反射特征的本征模态函数分量包括：

26、通过将信号分解为具有有限带宽的本征模态函数来实现信号的分离和提取，通过求解以下优化问题来实现：

27、

28、其中，s(t)表示单道地震数据，um(t)表示第m个本征模态函数，ωm表示第m个本征模态函数的中心频率，表示第m个本征模态函数的hilbert变换，进一步，使用下式所示的拉格朗日乘数法来解决上式优化问题：

29、

30、中心频率的值由平滑反射系数振幅谱的极值点的频率确定。

31、进一步的，采用同步挤压最优基小波变换分别计算每个二维本征模态函数分量的每个地震道，获得每个地震道的时频谱包括：

32、采用最优基本小波作为同步挤压变换框架内的基小波，最优基本小波通过三参数小波拟合地震子波获得，三参数小波在时域中的定义为：

33、

34、其中，σ、τ和β分别表示调制频率、能量衰减因子和能量延迟因子。λ＝(σ,τ,β)表示σ、τ和β的集合，

35、

36、基于上述方法的构思，本发明提供一种多尺度沉积旋回相空间精细表征系统，包括第一计算模块、第二计算模块、映射模块、时频谱计算模块以及表征模块；

37、第一计算模块用于计算二维地震数据平均傅里叶振幅谱和平均反射系数振幅谱；

38、第二计算模块采用尺度空间表示方法计算平滑的反射系数振幅谱，根据反射系数振幅谱与经验模态之间的关系，设置平滑反射系数谱的极值个数为本征模态函数分量的个数，极值频率为每个本征模态函数分量的中心频率；

39、映射模块采用变分模态分解方法对输入的二维地震数据进行分解，得到能够表征不同尺度地质构造的地震反射特征的本征模态函数分量；

40、时频谱计算模块采用同步挤压最优基小波变换分别计算每个二维本征模态函数分量的每个地震道，获得每个地震道的时频谱，

41、表征模块采用脊线提取方法从每个地震道的时频谱中提取瞬时主频曲线，获得二维瞬时主频属性剖面，利用瞬时主频属性剖面解释沉积旋回单元横向展布规律，即多尺度沉积旋回相空间精细表征。

42、本发明还可以提供一种计算机设备，包括处理器以及存储器，存储器用于存储计算机可执行程序，处理器从存储器中读取所述计算机可执行程序并执行，处理器执行计算可执行程序时能实现本发明所述多尺度沉积旋回相空间精细表征方法。

43、同时提供一种计算机可读存储介质，计算机可读存储介质中存储有计算机程序，所述计算机程序被处理器执行时，能实现本发明所述的多尺度沉积旋回相空间精细表征方法。

44、另外，本发明所述一种多尺度沉积旋回相空间精细表征方法还可以用于识别和解释从地震数据中提取沉积旋回信息。

45、与现有技术相比，本发明具有以下有益效果：

46、本技术考虑到地震反射数据中同时包含了不同尺度沉积层序地震反射信息。克服了传统方法无法有效分离并表征地震数据中蕴含的多尺度沉积旋回信息的问题。本技术通过改进变分模态分解方法能够有效的从地震数据中分离出不同尺度的地震反射波特征，在此基础上采用同步挤压最优基小波变换能够准确表征不同尺度沉积旋回的变化规律。结合脊提取方法提出的瞬时主频属性能够有效表征不同尺度沉积旋回的横向展布范围。本发明处理过程中的关键参数均从数据中提取，操作简单，计算速度快，适合海量地震数据处理，这为后续的层序地层学研究提供了重要工具。