一种存在站址误差及外校正源的直接定位方法与流程

本发明涉及辐射源定位，尤其涉及一种存在站址误差及外校正源的直接定位方法。

背景技术：

1、在传统两步定位方法中，需要从接收到的辐射源电磁信号中提取与其位置有关的信号参数，例如：到达角、到达时间、到达时差和到达频差，再根据提取出的信号参数对辐射源进行定位。直接定位指观测站基于接收到的辐射源电磁信号直接估计辐射源位置。

2、传统两步定位方法由于忽略了在所提取信号参数对应于一个辐射源的潜在约束，导致定位并不是最优的，而直接定位方法能够有效利用这一潜在约束，提升了对辐射源位置的定位。

3、现有技术中，对辐射源进行定位的直接定位方法不能随着应用环境进行适应性改变，在执行高精度定位的任务时，难以满足要求。

4、因此，亟需一种对辐射源进行定位的技术方案。

技术实现思路

1、鉴于上述的分析，本发明实施例旨在提供一种存在站址误差及外校正源的直接定位方法，用以解决现有技术中辐射源定位精度低的问题。

2、本发明实施例提供了一种存在站址误差及外校正源的直接定位方法，所述直接定位方法包括：

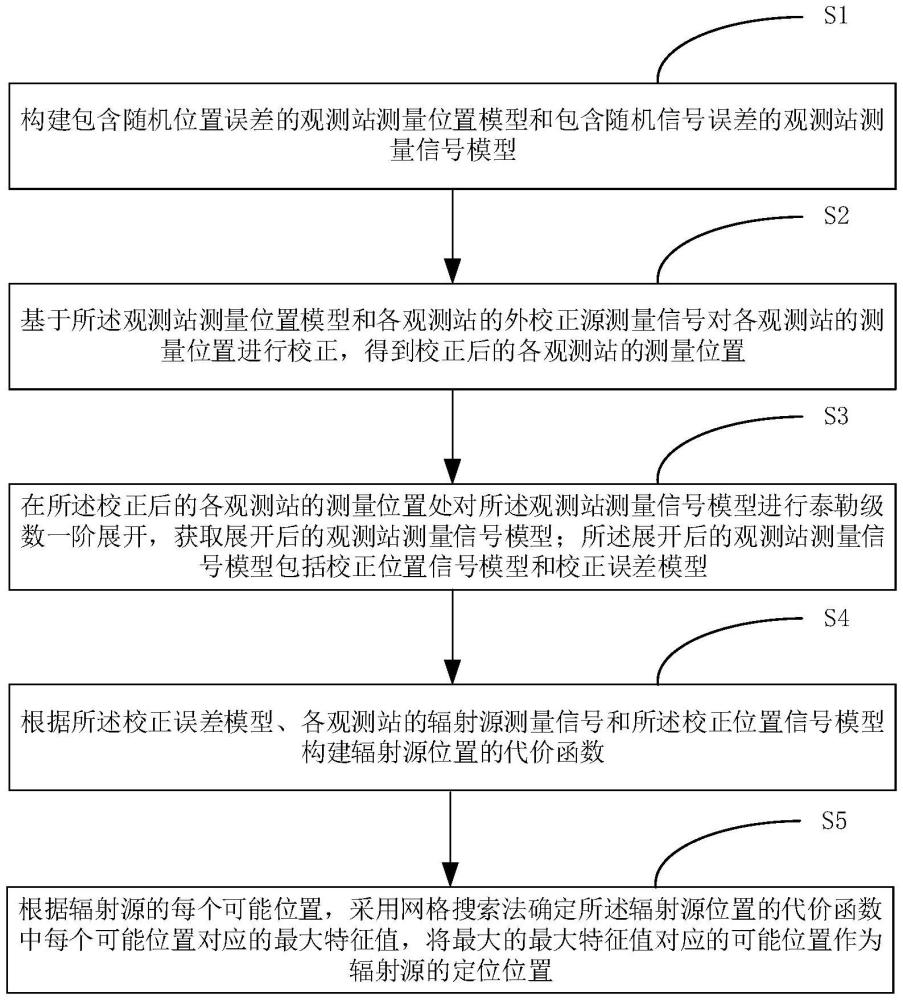
3、构建包含随机位置误差的观测站测量位置模型和包含随机信号误差的观测站测量信号模型；

4、基于所述观测站测量位置模型和各观测站的外校正源测量信号对各观测站的测量位置进行校正，得到校正后的各观测站的测量位置；

5、在所述校正后的各观测站的测量位置处对所述观测站测量信号模型进行泰勒级数一阶展开，获取展开后的观测站测量信号模型；所述展开后的观测站测量信号模型包括校正位置信号模型和校正误差模型；

6、根据所述校正误差模型、各观测站的辐射源测量信号和所述校正位置信号模型构建辐射源位置的代价函数；

7、根据辐射源的每个可能位置，采用网格搜索法确定所述辐射源位置的代价函数中每个可能位置对应的最大特征值，将最大的最大特征值对应的可能位置作为辐射源的定位位置。

8、基于上述方法的进一步改进，所述基于所述观测站测量位置模型和各观测站的外校正源测量信号对各观测站的测量位置进行校正，得到校正后的各观测站的测量位置，包括：

9、根据所述各观测站的外校正源测量信号，确定所述参考观测站和其他观测站中每一个观测站相对于外校正源位置的测量距离差方程；所述参考观测站为从所有观测站中任选的一个观测站；

10、基于各观测站的测量位置，确定所述参考观测站与其他观测站中每一个观测站相对于所述外校正源位置的理论距离差方程；

11、利用所述参考观测站和其他观测站中每一个观测站相对于外校正源位置的测量距离差方程和理论距离差方程，构建测量距离差和理论距离差的差值方程，求解所述差值方程得到各观测站的估计随机位置误差；

12、根据所述各观测站的测量位置和所述各观测站的估计随机位置误差，计算得到所述校正后的各观测站的测量位置。

13、基于上述方法的进一步改进，所述参考观测站和其他观测站中每一个观测站相对于外校正源位置的测量距离差方程为：

14、

15、其中，表示第i个观测站和参考观测站与外校正源的位置的测量距离差，v表示光速，表示外校正源测量信号到达第i个观测站和到达参考观测站的时间差，co表示所述外校正源的位置，分别表示参考观测站的实际位置、第i个观测站的实际位置，表示参考观测站和第i个观测站的测量误差；

16、所述参考观测站与其他观测站中每一个观测站相对于所述外校正源位置的理论距离差方程为：

17、

18、其中，表示第i个观测站与参考观测站的理论距离差，si、sl分别表示参考观测站的测量位置、第i个观测站的测量位置。

19、基于上述方法的进一步改进，所述构建测量距离差和理论距离差的差值方程，包括：

20、在各观测站的测量位置si处对进行泰勒级数一阶展开得到：

21、

22、

23、其中，表示由第i个观测站的测量位置si指向外校正源的位置co的单位矢量；

24、所述差值方程为：

25、

26、利用泰勒级数一阶展开后的对所述差值方程进行化简，化简后的所述差值方程为：

27、

28、其中，ψi、ψl分别为第i个观测站、参考观测站的随机位置误差。

29、基于上述方法的进一步改进，所述各观测站的估计随机位置误差为：

30、

31、其中，表示各观测站的估计随机位置误差，qβ表示ψ的协方差矩阵，表示观测站随机位置误差量的方差，i3m表示对角线元素为1、其余元素为0的3m×3m的矩阵；

32、gc为(m-1)×3m的矩阵且第(i-1)行为：

33、

34、其中，qc为的协方差矩阵；

35、其中，hc为(m-1)×1的矩阵且第(i-1)个元素为

36、所述校正后的各观测站的测量位置为：

37、

38、其中，表示校正后的各观测站的测量位置。

39、基于上述方法的进一步改进，所述观测站测量位置模型为：

40、s＝so+ψ；

41、

42、其中，表示m表示观测站的数量，s、so、ψ表示观测站的测量位置矢量、实际位置矢量、随机位置误差矢量；si、ψi分别表示第i个观测站的测量位置矢量、实际位置矢量、随机位置误差矢量；

43、随机位置误差矢量ψ符合零均值，并且ψ的协方差矩阵为：

44、

45、其中，qβ表示ψ的协方差矩阵，表示观测站随机位置误差量的方差，i3m表示对角线元素为1、其余元素为0的3m×3m的矩阵；

46、第i个观测站的测量位置矢量、实际位置矢量、随机位置误差矢量为：

47、si＝[xi,yi,zi]t；

48、

49、其中，xi、yi、zi分别表示第i个观测站的x轴测量坐标、y轴测量坐标、z轴测量坐标；分别表示第i个观测站的x轴实际坐标、y轴实际坐标、z轴实际坐标；分别表示第i个观测站的x轴随机误差量、y轴随机误差量、z轴随机误差量。

50、基于上述方法的进一步改进，所述观测站测量信号模型为：

51、z＝ηqr+w；

52、

53、其中，zi表示第i个观测站的采样点信号矢量，ηi表示第i个观测站的未知路径损耗因子，并且||ηi||＝1；wi表示第i个观测站的随机信号误差矢量；r表示辐射源信号矢量，并且||r||＝1；qi表示第i个观测站的离散傅里叶变换矢量；in表示对角线元素为1、其余元素为0的n×n的矩阵，n为各观测站辐对射源信号的采样点数量；

54、zi＝[zi[0],zi[1],...,zi[n-1]]t；

55、wi＝[wi[0],wi[1],...,wi[n-1]]t；

56、r＝[r[0],r[1],...,r[n-1]]t；

57、第i个观测站的离散傅里叶变换矢量为：

58、

59、n＝[0,1,...,n-1]t；

60、

61、其中，j表示虚数单位，δ表示各观测站的信号采样间隔，uo表示辐射源实际位置，表示第i个观测站的实际位置。

62、基于上述方法的进一步改进，所述展开后的观测站测量信号模型为：

63、

64、其中，表示所述校正位置信号模型，w″表示所述校正误差模型，diag{}表示对角矩阵。

65、基于上述方法的进一步改进，所述根据所述校正误差模型、各观测站的辐射源测量信号和所述校正位置信号模型构建辐射源位置的代价函数，包括：

66、计算所述校正误差模型的协方差矩阵；

67、基于所述校正误差模型的协方差矩阵、各观测站的辐射源测量信号和所述校正位置信号模型构建辐射源位置的加权最小二乘解方程；

68、基于辐射源位置的加权最小二乘解方程得到辐射源信号的估计值；

69、将所述辐射源信号的估计值代入辐射源位置的加权最小二乘解方程，得到辐射源位置的代价函数。

70、基于上述方法的进一步改进，所述校正误差模型的协方差矩阵为：

71、

72、其中，为对角线上最大元素；im表示对角线元素为1、其余元素为0的m×m的矩阵；分别表示第1个观测站、第i个观测站、…第m个观测站的随机信号误差的方差。

73、与现有技术相比，本发明至少可实现如下有益效果之一：

74、1、利用各观测站的外校正源测量信号对各观测站的位置进行快速校正，基于校正后的各观测站的位置对辐射源进行直接定位，同时考虑了校正后的各观测站的站址残余误差，实现了对辐射源位置的精准定位；

75、2、根据各观测站的外校正源测量信号确定参考观测站与其他观测站的测量距离差方程，同时基于各观测站的测量位置确定参考观测站与其他观测站的理论距离差方程，最后根据测量距离差方程和理论距离差方程估计得到校正后的各观测站的位置，提升对辐射源的定位精度；

76、3、利用在校正后的各观测站的位置对观测站测量信号模型进行展开，构建辐射源位置的代价函数，提升对辐射源位置的定位精度。

77、本发明中，上述各技术方案之间还可以相互组合，以实现更多的优选组合方案。本发明的其他特征和优点将在随后的说明书中阐述，并且，部分优点可从说明书中变得显而易见，或者通过实施本发明而了解。本发明的目的和其他优点可通过说明书以及附图中所特别指出的内容中来实现和获得。