本发明涉及轴承故障诊断,尤其是一种基于非线性模态分解的变转速轴承故障诊断方法。
背景技术:
1、滚动轴承是旋转机械设备中常用的零部件,其健康状态关系着设备运行的可靠性与稳定性。然而,滚动轴承在变转速运行时,受工况影响更容易发生故障,进而导致严重的安全问题和高昂的维护成本。因此,准确诊断变转速滚动轴承状态具有极其重要的意义。变转速运行下故障特征频率会受转速调制,导致直接利用振动信号包络分析无法有效的判断轴承的故障情况。
2、阶次跟踪算法是目前研究变转速轴承故障诊断的主要方法之一,其核心在于跟踪获取轴承的等角度采样信号。目前,阶次跟踪算法主要包括硬件阶次跟踪、计算阶次跟踪和无转速计阶次跟踪。硬件阶次跟踪方法是直接利用光电脉冲角度编码盘进行等角度采样,获取角域信号,该方法实时性较好;然而其成本较高,硬件设备复杂,不利于安装。计算阶次跟踪是通过键相装置获取转速信号,然后根据转速信号计算等角度重采样时间点,之后通过插值算法获得角域信号;但安装键相装置会提高设备的复杂性,尤其是在传动系统中安装更为艰难。无转速计阶次跟踪主要是利用时频域分析方法从振动信号中直接提取出轴承的转速信号,然后利用等角度采样获得角域信号;该方法无需安装其它测量设备,节省成本和设备空间。在强噪声环境下,大多时频分析方法难以保证转速信号的准确性。
技术实现思路
1、针对现有技术的不足,本发明提供一种基于非线性模态分解(nonlinear modedecomposition,nmd)的变转速轴承故障诊断方法,目的是提升强噪声环境下时频分析精度,保证转速信号的准确性,提高故障诊断的准确性。
2、本发明采用的技术方案如下:
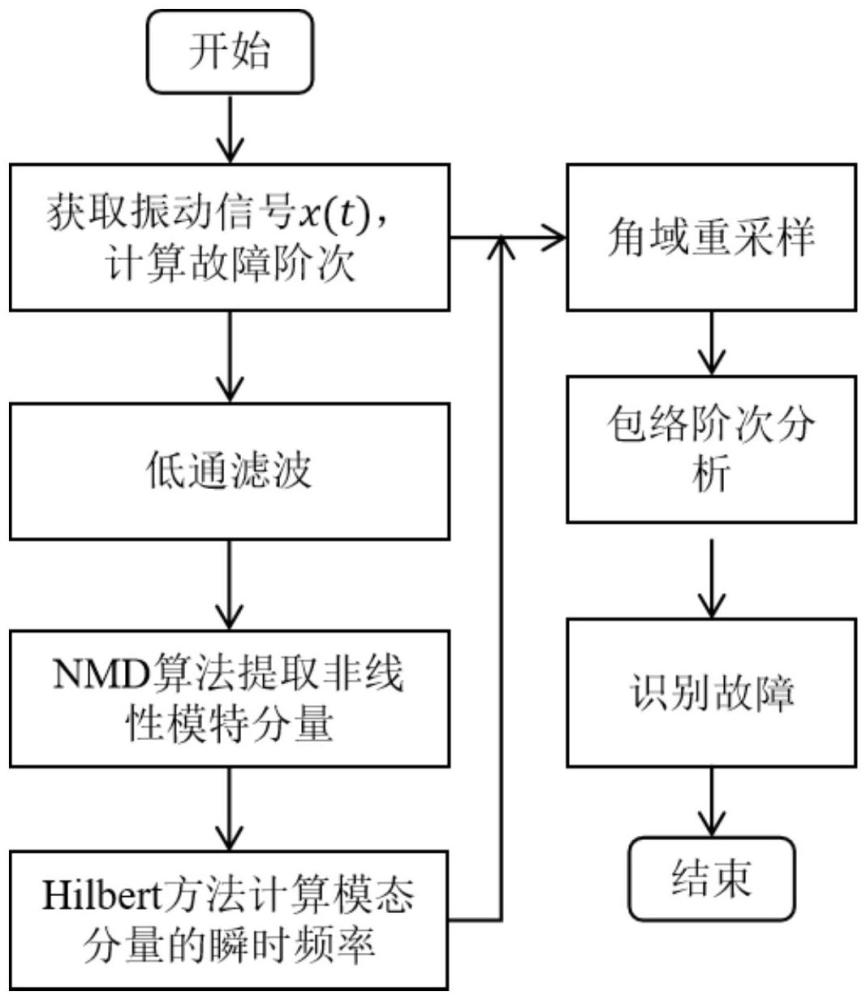
3、一种基于非线性模态分解的变转速轴承故障诊断方法,包括:
4、s1、获得变转速下滚动轴承的振动信号,并根据轴承参数计算故障特征阶次;
5、s2、将所述振动信号进行低通滤波,获得滤波后信号;
6、s3、利用非线性模态分解在所述滤波后振动信号的低频部分提取非线性模态分量;
7、s4、利用hilbert方法计算模态分量的瞬时频率;
8、s5、基于所述瞬时频率,利用角域重采样方法将s1获得的振动信号转化为角域伪平稳信号;
9、s6、对所述角域伪平稳信号通过包络阶次分析,求出解析信号的模,再对解析信号的模求傅里叶谱,对比傅里叶谱和所述故障特征阶次,识别故障。
10、进一步技术方案为:
11、步骤s3中,所述非线性模态分解包括:
12、s31、利用短时傅立叶变换或小波变换获取信号的时频表示;
13、s32、提取时频表示中的时频脊曲线;
14、s33、提取到时频脊曲线后,进行谐波重构:对主谐波利用脊线法重构,对次谐波采用脊线法和直接法中不一致系数较大的方法进行重构;
15、s34、次谐波检验真假:利用谐波重构方法获得第h次的次谐波rh(t)后,通过零假设的独立性分析辨别其真伪,h≥2;
16、s35、噪声检验:当分解至所剩信号被判断为噪声,停止迭代。
17、步骤s32中,在短时傅立叶变换下,将使路径泛函最大化的峰序列作为时频脊曲线,峰序列表达式如下:
18、
19、其中,gs(·)为短时傅立叶变换的时频表示,ωp(t)代表时频脊曲线,std[·]代表求标准差,mean[·]代表求均值,δωp(tn)=ωp(tn)-ωp(tn-1),tn代表第n个时刻。
20、步骤s33中,提取时频脊曲线ωp(t)后,进行谐波r(t)的幅值a(t)、相位频率的提取,实现对谐波的重构;
21、对于采用短时傅立叶变换获得时频表示的情况,脊线法重构方法为:
22、
23、对于采用小波变换获得时频表示的情况,脊线法重构方法为:
24、
25、其中,ws(·)为小波变换的时频表示;δvd和δlnvd为离散化效应的修正值,为短时傅里叶变换的窗函数的傅里叶变换,ωψ为小波峰值频率,ψ*(t)为小波变换的对数正态小波基函数ψ(t)的复共轭函数。
26、所述零假设的独立性分析,包括:给定最大时移m,确定r1(t)谐波的代理参数:
27、
28、式中,n为采样长度;fs为采样频率;d为时移点数;δtd代表时间间隔;
29、对于rh(t)次谐波,h≥2,首先将时频信号前移δtd/2,然后利用谐波重构法获得最优参数为rh(t)的代理参数;
30、用统计参数量化rh(t)和r1(t)的一致性:
31、
32、对谐波之间相互一致性进行总体度量:
33、
34、其中,wa,wv,wφ为权重系数;
35、若的置信水平小于预设置信水平,则此谐波为伪谐波,否则为真谐波;为δt0=0时一致性的总体度量,为时移点数为d时的一致性的总体度量。
36、步骤s35,所述噪声检验包括:
37、计算本次迭代的主谐波噪声检验统计特征d0;
38、生成ns个代理数据,计算每个代理数据对应的时频表示,从中提取分量,并计算各自相应的噪声检验统计特征当ds>d0的代理数据个数比例高于设置的显著性水平,则拒绝检验噪声的零假设。
39、步骤s4中,所述利用hilbert方法计算模态分量的瞬时频率,包括:
40、将信号经hilbert变换后获得对应的解析信号;
41、计算解析信号的幅值和相位;
42、计算所述相位对于时间的倒数作为所述瞬时频率。
43、步骤s5中,所述基于所述瞬时频率,利用角域重采样方法将s1获得的振动信号转化为角域伪平稳信号,包括:
44、按照等角度采样间δθ对原始振动信号x(t)基于三次样条插值的角域重采样,获得t(i)时刻的旋转总角度:
45、
46、其中,fr(t)为转速信号,即s4获得的瞬时频率;i代表时间序列中点的标号;
47、利用三次样条插值对t(i)和t(i+1)间的角度θ和时间t进行拟合:
48、θi(t)=a3(t-t(i))3+a2(t-t(i))2+(t-t(t))+a0
49、其中,a0、a2、a3分别为拟合系数;
50、当θ(i)≤kδθ<θ(i+1),则计算时域振动信号中第k个等角度采样的时刻t(k):
51、
52、对x(t)进行插值运算可以得到t(k)时间点振动幅值a(k),从而获得角度序列为δθ,2δθ,…,kδθ,幅值序列为a(1),a(2),...,a(k)的角域信号。
53、步骤s2中,低通滤波时截止频率根据轴承的转速工作范围确定。
54、步骤s1中,故障特征阶次包括内圈故障特征阶次:
55、
56、外圈故障特征阶次:
57、
58、滚动体故障特征阶次:
59、
60、其中,z为滚动体个数,d表示滚动体直径,d表示节径,α为接触角。
61、本发明的有益效果如下:
62、本发明通过nmd方法提取轴承的转动过程中的低频非线性模态分量,通过hilbert方法计算瞬时频率,获取轴承的转速信息,利用角域重采样方法将时域的变转速非平稳信号转化为角域伪平稳信号,通过包络阶次分析实现变转速轴承的故障的准确判断。本发明方法具有较好的抗噪性能,无需安装其它测量设备,节省了成本和设备空间。
63、本发明的其它特征和优点将在随后的说明书中阐述,或者通过实施本发明而了解。
