一种基于四元互补格雷码辅助相位展开的三维测量方法

本发明涉及非接触式三维测量领域，尤其涉及一种基于四元互补格雷码辅助相位展开的三维测量方法。

背景技术：

1、光学三维测量是一种非常有效并且具有高精度的非接触式三维检测手段，在精密器械的高精度测量、计算机视觉和医学等领域有着非常广泛的应用。

2、而结构光投影法是当下较为流行的一种非接触式测量方法。条纹投影轮廓术(fpp)是其中最具代表性的一种方法，具有高精度，高灵活性的优点。由于相位提取的过程中使用了反正切函数，描述物体高度信息的相位信息是被包裹的，因此需要对包裹相位进行相位展开。

3、常见的相位展开方法可以分为空间相位展开和时间相位展开，其中时间相位展开相较而言具有更好的抗噪性，同时也更加适用于复杂场景，因此被广泛的使用。在时间相位展开方法中，基于格雷码的方法鲁棒性高，抗噪性较好，因此相位展开的正确率较高。但是常规格雷码是二元的，其方法需要额外投影大量图案进行测量，影响了测量效率。事实上，可以通过提升格雷码的灰度进制来提高测量效率，例如使用三元格雷码或四元格雷码。其中四元格雷码的码字确定具有挑战且相邻码字边界更加容易出现错误。此外，格雷码灰度进制的提升也会导致其抗噪性下降。

4、因此，有必要提供一种基于四元互补格雷码辅助相位展开的三维测量方法解决上述技术问题。

技术实现思路

1、本发明提供一种基于四元互补格雷码辅助相位展开的三维测量方法，能够很大限度的提升测量效率的同时保证测量精度。

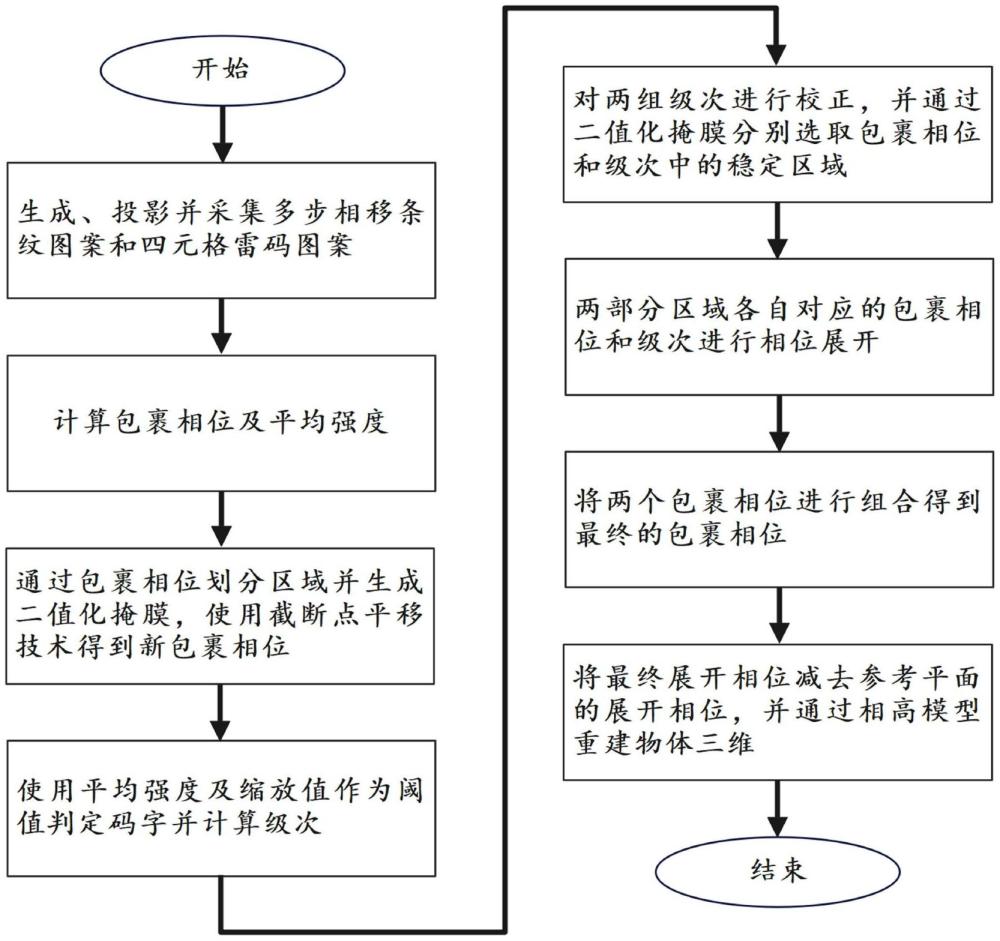
2、本发明提供的基于四元互补格雷码辅助相位展开的三维测量方法包括以下步骤：

3、s1、由投影仪投影并由相机捕捉预先设计好的多步相移条纹图和四元格雷码图；

4、s2、使用多步相移图案计算包裹相位及条纹图案的平均强度；

5、s3、根据包裹相位的相位值将包裹相位划分为中心稳定区域和截断不稳定区域，并生成两个区域的二值化掩膜，并使用截断点平移技术得到一个新的包裹相位；

6、s4、使用平均强度及其缩放值作为不同的阈值，使用不同的阈值线将最后一幅四元格雷码图案解算为两组二元码字，其它格雷码图案解算成四元码字；根据所获得的码字计算出两组级次；

7、s5、使用一种基于连通区域标记算法的策略对两组级次进行校正，并通过两个二值化掩膜分别选取两组包裹相位和级次中较为稳定的部分；

8、s6、分别将两组包裹相位和级次的对应区域进行相位展开，得到两个只有一半区域的展开相位；

9、s7、将两个只有一半区域的展开相位进行组合得到最终的展开相位；

10、s8、将最终的展开相位减去参考平面的展开相位，再通过相高模型将相位信息转换成高度信息。

11、优选的，所述s1包括以下具体步骤：

12、s11：计算机生成获得相位所需的多步相移条纹图像；

13、s12：计算机生成获得级次信息所需要的四元格雷码图案；

14、s13：使用抖动算法将生成的多步相移条纹和四元格雷码图案二值化；

15、s14：投影仪保持一定的离焦程度，确保所投影的二值化后的多步相移条纹图案呈现正弦性；

16、s15：相机采集变形相移条纹图案和四元格雷码图案。

17、优选的，所述s2的具体步骤如下：

18、s21：根据s1步骤获得的变形条纹，其表达式为：

19、

20、其中，α是相机灵敏度，r是物体的反射率，(x,y)是相机空间中的像素坐标；a和b分别是投影条纹的平均强度和调制强度，通常情况下，当投影仪的灰度范围为[0,255]时，为了覆盖整个动态范围，一般设定为a＝b＝127.5；φ是包含了被测物体的高度信息的相位；n表示相移的索引，且n＝0,1,…,n-1，n代表相移步数；β1是照明物体的环境光，β2是直接进入相机的环境光；上述式子可以进一步简写为更常用到的式子：

21、

22、a(x,y)＝α{r(x,y)[a+β1(x,y)]+β2(x,y)}

23、b(x,y)＝αr(x,y)b

24、其中a(x,y)是平均强度，b(x,y)是调制强度；

25、s22：使用获得的变形条纹图像计算包裹相位，计算公式为：

26、

27、使用上述公式计算获得包裹相位之后，后续需要使用格雷码图案获得级次，将包裹相位进行相位展开；

28、s23：使用获得的变形条纹图像计算平均强度，计算公式为：

29、

30、其中i1,i2,...,in为采集到的多步相移条纹图像。

31、优选的，所述s3的具体步骤如下：

32、s31：根据包裹相位的相位值将包裹相位划分为中心稳定区域和截断不稳定区域，并生成两个区域的二值化掩膜，计算公式为：

33、

34、maskedge(x,y)＝1-maskmid(x,y)

35、其中maskmid(x,y)和maskedge(x,y)代表中心稳定区域和截断不稳定区域所对应的二值化掩膜，下标‘mid’和‘edge’分别代表中心稳定区域和截断不稳定区域；

36、s32：对原包裹相位使用截断点平移技术得到一个新的包裹相位，计算公式为：

37、

38、

39、代表截断点平移后的新包裹相位。

40、优选的，所述s4的具体步骤如下：

41、s41：由于使用四元进行编码，所以需要三幅阈值分布才能进行解码；理想情况下阈值的表达式为：

42、

43、thm(x,y)＝a(x,y)

44、

45、其中thu(x,y)、thm(x,y)及thl(x,y)为图像分割所需要的阈值分布；

46、然而，在实践中，ab阈值策略并不适用于所有场景；例如，在高速测量需求下，投影的条纹为二值化抖动图案，通过物理散焦生成相对的正弦条纹；在这种情况下，散焦条纹的调制强度b会降低，这会导致基于条纹的ab阈值策略无法准确分割格雷码的灰度级别；但是我们注意到，散焦条纹的平均强度a并不会发生改变，而散焦条纹的平均强度a近似等于未散焦状态下的调制强度b,证明如下：

47、一般测量的环境为暗室，环境光的影响较小，步骤s21公式中的β1、β2可以忽略，因此可以得到：

48、

49、因此原本阈值表达式中的b可以通过γa进行替换；通过a阈值策略获得的阈值表达式为：

50、

51、thm(x,y)＝a(x,y)

52、

53、值得说明的是，由于a与b一般设定为相同值127.5，所以通常情况下γ＝1；

54、s42：将最后一幅四元格雷码采用不同的阈值线分解为两组不同的二元码字，其余格雷码分解为四元码字；公式如下：

55、

56、其中g′m(x,y)和g″m(x,y)分别代表两组二元码字信息，m代表四元格雷码图案的数量，graym(x,y)代表最后一张四元格雷码图案；gm(x,y)代表四元码字信息，graym代表除最后一张格雷码图案外的其余格雷码图案，m代表格雷码图案及码字信息索引，注意m＜m；

57、s43：在获得码字信息之后，可计算级次，计算公式为：

58、

59、k(x,y)＝f(v(x,y))

60、

61、w′(x,y)＝g(v′(x,y))

62、k′(x,y)＝ceil(w′(x,y)/2)

63、其中v(x,y)和v′(x,y)代表直接计算得到的码字，f(·)和g(·)代表重排序运算，k(x,y)和w′(x,y)代表重排序后得到的码字，ceil(·)代表向上取整运算，k(x,y)和k′(x,y)是最终的级次。

64、优选的，所述s5的具体步骤如下：

65、s51：对两组级次分别逐级次使用连通区域标记算法，并对面积大小为1个像素点大小的连通域采取邻域判定的方式进行校正；

66、s52：通过两个二值化掩膜分别选取两组包裹相位和级次中较为稳定的部分，计算公式为：

67、

68、kmid(x,y)＝maskmid(x,y)·k(x,y)

69、k′mid(x,y)＝maskedge(x,y)·k′(x,y)

70、其中下标‘mid’和‘edge’表示当前包裹相位和级次所对应的区域，除对应区域外的值均置为0。

71、优选的，所述s6的具体步骤如下：

72、s6：分别将两组包裹相位和级次的对应区域进行相位展开，得到两个只有一半区域的展开相位，计算公式为：

73、

74、注意所直接计算出的包裹相位应该额外增加π，此时两个只有一半区域的展开相位的下标‘mid’和‘edge’是相对于而言的。

75、优选的，所述s7的具体步骤如下：

76、s7：将两个只有一半区域的展开相位进行组合得到最终的展开相位,计算公式为：

77、φ(x,y)＝φmid(x,y)∪φedge(x,y)

78、优选的，所述s8的具体步骤如下：

79、s81、将最终的展开相位减去参考平面的展开相位，计算公式为：

80、δφ(x,y)＝φ(x,y)-φr(x,y)

81、其中φr(x,y)和δφ(x,y)分别表示参考平面的展开相位和仅包含物体高度信息的展开相位；

82、s82、通过相高模型将相位信息转换成高度信息，计算公式为：

83、δφ2＝ahδφ2+bhδφ+ch

84、为了方便表示，(x,y)将被省略；其中h表示待测物体的高度，a、b和c为系统参数，在标定过程中获得。

85、与相关技术相比较，本发明提供的基于四元互补格雷码辅助相位展开的三维测量方法具有如下有益效果：

86、本发明提供一种基于四元互补格雷码辅助相位展开的三维测量方法，该方法投射多步相移条纹图像和四元格雷码图案。利用四元格雷码信息容量大的优势，将最后一幅四元格雷码图案解算为两幅二元格雷码图案，一张用做计算级次，另一张用于引入互补策略。无需额外投影图案的前提下引入了互补测量，提高了测量效率的同时，保证了相位展开的正确率。同时，引入了基于连通区域标记算法的孤立级次校正策略，以应对由于格雷码灰度级增加导致其抗噪性能下降从而可能发生的级次错误。本方法具有测量效率高，鲁棒性较好，测量结果精度高等优点。