一种可实时高精度相对测量的并排多星编队方法与流程

本发明涉及一种可实时高精度相对测量的并排多星编队方法，属于空间。

背景技术：

1、分布式卫星编队的星间基线测量需要对观测编队中的两两卫星形成的多条基线同时测量。当前在轨应用的基于gnss测量的基线测量方法，其精度满足不了三维成像应用需求，在此基础上引入激光/视觉测量方法，利用测量系统视场内视线方向靶标位置的精确测量，可将测量精度大幅提高。面对多于两颗星的多星编队系统，编队卫星在飞行过程中会存在共线一字形排列情况，由于中间卫星的遮挡，使得两端卫星存在共视遮挡，从而激光和视觉测量系统无法完成远端两星的基线测量。

技术实现思路

1、本发明解决的技术问题是：克服现有技术的不足，提出一种可实时高精度相对测量的并排多星编队方法，利用空间相对运动学模型建立星间基线数学模型，建立基线与轨道六根数的对应关系，并作为编队构型设计和编队卫星在轨实时调整的依据，为多星多基线测量时避免存在共视遮情况提供解决方法。

2、本发明的技术方案是：一种可实时高精度相对测量的并排多星编队方法，包括：

3、基于轨道运动学理论建立编队多星相对运动的数学模型，通过相对运动推导简化建立星间基线数学模型，获得基线矢量与轨道六根数关系的数学表达式，建立编队系统基线要求与轨道参数的直接对应关系；

4、建立基线测量系统视场要求对基线矢量的约束关系；

5、编队构型和轨道设计时，多星分布式编队中的卫星两两为一组，根据基线要求利用对应关系获得分布式编队卫星中的任意两个卫星的相对轨道参数，同时利用视场要求对基线矢量的约束关系修正两组卫星的相对轨道参数，以一颗卫星作为主星设计轨道初始参数，从而根据上述相对轨道参数得到编队的其余几颗卫星的初始轨道参数；

6、在轨运行时，通过gnss实时解算轨道参数，按照数学表达式获得分布式编队的任意两颗卫星形成的空间基线，利用视场要求对基线矢量的约束关系判断多颗卫星形成的多组基线是否存在共视遮挡，若存在共视遮挡，则利用视场要求对基线矢量的约束关系在轨调整其中一组的编队卫星轨道参数使得任意两组基线满足约束关系，从而实现任意时刻并排多星编队的实时高精度相对测量。

7、所述基于轨道运动学理论建立编队多星相对运动的数学模型，通过相对运动推导简化建立星间基线数学模型，获得基线矢量与轨道六根数关系的数学表达式，建立编队系统基线要求与轨道参数的直接对应关系，包括：

8、建立航天器主星rtn坐标系；则rtn坐标系下从星相对于主星的相对运动表达式为：

9、δrr＝aa-ac+ac[-(ea cosωa-ec cosωc)cosuc-(ea sinωa-ec sinωc)sinuc]

10、

11、δrn＝ac[-(ωa-ωc)sinic cosuc+(ia-ic)sinuc]

12、其中，uc是主星的平纬度幅角，uc＝ωc+mc，mc是平近点角，ωc和rc分别是主星的升交点赤经和地心距离，ic是主星的倾角，ec是主星的偏心率，ac是主星的半长轴；aa、ea、ua、ma、ωa、ia和ra从星的轨道变量，物理意义与上述主星对应；

13、令aa－ac＝0，ua－uc＝0，以虚拟星o为主星，主星为圆轨道，ec＝0，简化从星相对于主星的相对运动表达式，得到

14、δrr＝-acea cos(uc-ωa)

15、δrt＝2acea sin(uc-ωa)

16、

17、其中，

18、按编队系统的星间基线需求考虑，不考虑法向n方向基线分量，每一组基线的两颗卫星m1、s2与虚拟星o在同一直线的两端，且两颗卫星与虚拟星o的距离相等，此时需要两颗卫星的偏心率相等，即ea1＝ea2，同时两颗卫星的近地点幅角相差180°，即ωa1＝ωa2-180°；其中脚标1，2分别代表编队中的卫星m1和卫星s2；

19、计算得到星间基线在rtn坐标系下的r-t平面内的分量表达式，得到基线长度和基线倾角。

20、所述基线长度和基线倾角表达式分别为：

21、径向r方向基线长度bz：

22、bz＝2δrr＝-2acea1cps(uc-ωa1)，

23、飞行方向t方向基线长度bx：

24、bx＝2δrt＝4acea1sin(uc-ωa1)

25、基线倾角α：

26、

27、α＝arctan(-0.5cot(uc-ωa1))。

28、所述建立航天器主星rtn坐标系，包括：编队飞行相对运动坐标系定义为，坐标系原点为主星航天器，r方向为地球质心指向主星方向，t方向为主星的运动方向，n方向为垂直轨道面法向方向由右手系确定。

29、所述建立基线测量系统视场要求对基线矢量的约束关系，包括；

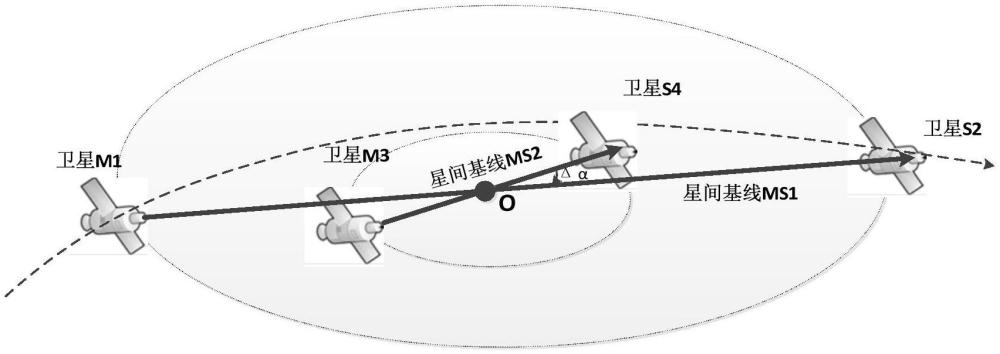
30、建立基线测量系统视场要求对基线矢量的约束关系,以虚拟星o为中心，编队卫星m1、m3…位于中心o的同一侧，编队卫星s2、s4…位于中心o的另一侧，其中m1、s2为一组形成空间基线ms1，m3、s4为一组形成空间基线ms2…依此类推；其中，基线ms1和基线ms2的基线倾角差的表达式如下：

31、δα＝arctan(-0.5cot(uc-ωa3))-arctan(-0.5cot(uc-ωa1))根据上述规律，基线倾角差δα的变化范围为其中δω＝ωa3-ωa1，脚标1、3分别代表卫星m1和卫星m3；

32、δα≥θ

33、其中，θ代表基线测量系统的最大视场角；

34、则，

35、δω＝ωa3-ωa1≥2θ；

36、即卫星m3和卫星m1的近地点幅角差要求大于2倍视场角。

37、所述根据基线要求利用对应关系获得分布式编队卫星中的任意两个卫星的相对轨道参数，同时利用视场要求对基线矢量的约束关系修正两组卫星的相对轨道参数，以一颗卫星作为主星设计轨道初始参数，从而根据上述相对轨道参数得到编队的其余几颗卫星的初始轨道参数，包括：

38、通过遥感卫星回归特性和观测效能需求，半长轴ac的大小通过任务计算给出，轨道倾角和升交点赤经也通过任务计算给出；对于任意一组构成基线的两颗卫星，通过任务需求给出径向r方向基线最大长度bz，即得到两颗卫星的偏心率ea1和ea2表示卫星m1、卫星s2的偏心率；同理可获得卫星m3、卫星s4的偏心率ea3和ea4；

39、通过任务需求给出并排多星的基线达到最大长度bz对应的uc的值u0，进而得到卫星m1的纬度幅角ωa1＝u0，卫星s2的纬度幅角满足ωa2＝ωa1+180°；

40、根据测量系统的视场约束关系，两对卫星形成的基线ms1和ms2的基线倾角差δα的约束，即δα≥2θ，θ由任务需求给定，能够确定δω≥2θ，由于双基线夹角δα越小观测效果越好，则δω＝2θ，ωa3＝ωa1+2θ，ωa4＝ωa3-180°；通过条件ua－uc＝0，获得每颗卫星初始平近点角ma＝ua-ωa；至此获得编队卫星的初始轨道参数。

41、所述若存在共视遮挡，则利用视场要求对基线矢量的约束关系在轨调整其中一组的编队卫星轨道参数使得任意两组基线满足约束关系，包括：通过gnss导航实现星间基线ms1和ms2的实时测量，获得ms1和ms2基线方向的差δα，利用基线测量系统视场要求对基线矢量的约束关系判据，具体调整四颗星的近地点幅角ωa1、ωa2、ωa3、ωa4，从而实现编队系统多星共视遮挡的星上自主规避。

42、所述具体调整四颗星的近地点幅角ωa1、ωa2、ωa3、ωa4，包括：以卫星m1的纬度幅角ωa1作为参考，卫星s2的纬度幅角满足ωa2＝ωa1+180°；利用δω＝2θ的关系，调整ωa3＝ωa1+2θ，ωa4＝ωa3-180°。

43、本发明与现有技术相比的优点在于：

44、(1)本发明建立了分布式编队卫星系统星间基线与轨道参数的数学关系模型，为三维成像观测任务的编队系统轨道参数设计提供理论方法。

45、(2)本发明建立了基线测量系统视场要求对星间基线矢量的约束关系，应用于分布式编队卫星轨道参数理论设计和在轨实时轨道调整。

46、(3)实际在轨运行中，本发明通过gnss信息实时解算的轨道参数判断多星是否存在共视遮挡，以此完成轨道参数的调整，满足多星星间基线实时测量的要求。

47、(4)本发明构建的方法，可以解决分布式多星系统编队构型的基线设计问题，同时解决运行时的基线共视遮挡问题，在轨运行时全过程可星上自主任务规划及执行，效率高、速度快，有助于任务灵活应对，具有实际工程意义。