本发明涉及地球物理勘探,具体涉及一种基于双重赋存模式耦合的广义权重方程估算水合物饱和度的方法、装置及电子设备。
背景技术:
1、天然气水合物是由天然气和水在高压低温条件下形成的冰状晶体化合物,广泛分布于陆地永久冻土带和大陆边缘深水盆地的沉积物中(kvenvolden,1993),是未来最具潜力的替代能源资源(boswell和collett,2011)。另一方面,水合物在地层温压条件变化的情况下极易发生分解,进而诱发海底地质灾害(archer等,2009)和加剧全球气候变暖(sultan等,2004)。准确预测水合物含量和分布不仅是定量评价水合物资源潜力和应对气候环境危害的基础,还是认识水合物成藏机理和指导水合物成功开采的重要前提。利用水合物储层地震弹性特征可以估算水合物饱和度(lee等,2008;best等,2013;wang等,2016;pan等,2019;liu等,2020),但是水合物饱和度和赋存形态之间的弹性耦合效应直接影响水合物储层表征精度。因此,深入理解水合物对地层声学特性的影响是水合物储层定量刻画的关键。
2、岩石物理模型建立了水合物饱和度和微观赋存形态与弹性响应特征之间的量化关系,为描述地震弹性响应特征和估算水合物饱和度奠定理论基础。由于孔隙充填(水合物充填在孔隙空间中)和骨架支撑(水合物支撑骨架颗粒)是最常见的两种水合物赋存类型,前人提出了许多针对这两类水合物储层的岩石物理模型。早期简单实用的经验模型,如wyllie时间平均方程、wood方程和三相权重方程,经常用于描述水合物储层弹性响应与水合物饱和度之间的关系。然而,这些模型缺少物理含义、未考虑微观分布模式,需要利用大量的实测数据对模型参数进行校正(刘欣欣等,2018)。比如,考虑水合物微观分布模式,部分理论模型,如接触模型(dvorkin等,1999;helgerud等,1999)、sca-dem模型(chand等,2006)、改进biot-gassmann理论(lee等,2004)和简化三相方程(lee等,2008),也成功应用于将速度信息转化为水合物饱和度(terry和knapp等,2018;pan等,2022)。然而,这些模型涉及模型参数较多,并且大多是基于单一赋存形态假设建立的,难以准确描述多种赋存形态共存型水合物地层。因此,有必要建立简单实用且耦合多种赋存形态水合物的岩石物理理论。
技术实现思路
1、本发明的目的在于提供一种基于双重赋存模式耦合的广义权重方程估算水合物饱和度的方法、装置及电子设备,以解决上述背景技术中提出的问题。
2、为了实现上述目的,本发明采用如下技术方案:
3、第一方面,提供了一种基于双重赋存模式耦合的广义权重方程估算水合物饱和度的方法,包括:
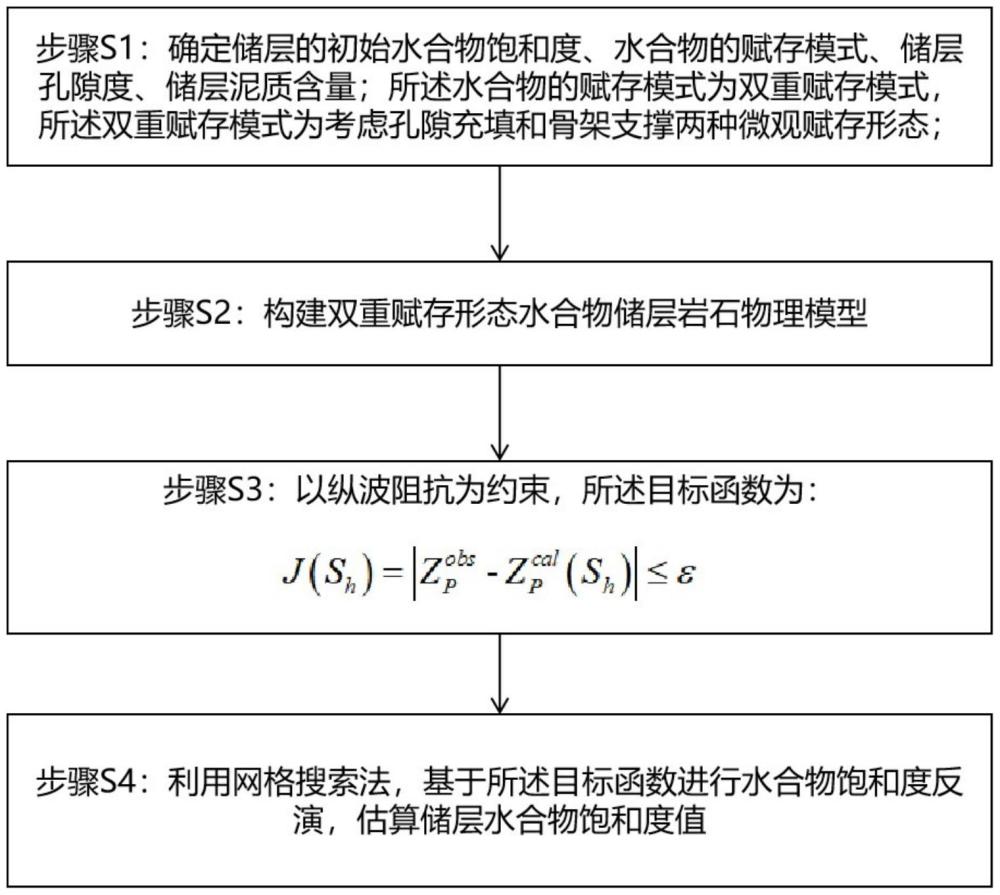
4、步骤s1:确定储层的初始水合物饱和度、水合物的赋存模式、储层孔隙度、储层泥质含量;
5、所述水合物的赋存模式为双重赋存模式,所述双重赋存模式为考虑孔隙充填和骨架支撑两种微观赋存形态;
6、步骤s2:构建双重赋存形态水合物储层岩石物理模型;
7、步骤s3:以纵波阻抗为约束构建目标函数,所述目标函数为:
8、
9、式中:和为纵波阻抗实际值和纵波阻抗预测值;ε为给定最小误差;
10、步骤s4:利用网格搜索法,基于所述目标函数进行水合物饱和度反演,估算储层水合物饱和度值。
11、进一步地,步骤s2中构建双重赋存形态水合物储层岩石物理模型包括:
12、步骤s21:利用hill平均计算固体矿物与骨架支撑型水合物相结合组成的岩石基质体积模量和剪切模量,所述固体矿物包括:石英、方解石、黏土;
13、步骤s22:利用基于双重赋存形态耦合的广义权重方程计算岩石基质与水和孔隙充填型水合物组成的饱和岩石体积模量和剪切模量。
14、进一步地,步骤s22中利用基于双重赋存形态耦合的广义权重方程计算岩石基质与水和孔隙充填型水合物组成的饱和岩石体积模量和剪切模量,其中:
15、基于双重赋存形态耦合的广义权重方程为:
16、
17、式中:zp,w、zp,h、zp,ma和zp分别为水、水合物、岩石基质和饱和岩石的纵波阻抗;ρw、ρh、ρma和ρb分别是水、水合物、岩石基质和饱和岩石的密度,
18、ρb=(1-φ)(1-vsh)ρsd+(1-φ)vshρc+φshρh+φ(1-sh)ρw;
19、φe为有效孔隙度,φe=φ-φshfms;其中:φ、fms和sh分别为孔隙度、骨架支撑形态百分比和水合物饱和度;
20、shpfe为孔隙充填型水合物饱和度,shpfe=sh(1-fms)/[1-sh+sh(1-fms)];swe为归一化后的含水饱和度,swe=(1-sh)/[1-sh+sh(1-fms)];
21、j为水合物地层的固结系数,反映水合物地层固结程度,j越小,地层固结程度越好。进一步地,步骤s21还包括岩石基质纵波阻抗计算:固体矿物与骨架支撑型水合物相结合组成岩石基质,共同起到应力支撑作用,在已知各种矿物组分的体积分数和弹性模量时,利用hill平均计算岩石基质体积模量和剪切模量:
22、
23、式中,ksd、kc、kh,ms和μsd、μc、μh,ms分别为石英、黏土和骨架支撑型水合物的体积模量和剪切模量;fsd、fc和fh,ms分别为石英、黏土和骨架支撑型水合物的体积分数,其中fsd=(1-φ)(1-vsh)/(1-φ+fmsshφ),fc=(1-φ)vsh/(1-φ+fmsshφ),fh,ms=fmsshφ/(1-φ+fmsshφ),φ、vsh、fms和sh分别为孔隙度、泥质含量、骨架支撑形态百分比和水合物饱和度;
24、利用岩石物理体积模型,岩石基质密度可以表达为:
25、ρma=fsdρsd+fcρc+fh,msρh
26、式中,ρsd、ρc和ρh分别为石英、黏土和水合物的密度。
27、岩石基质纵波阻抗表达式如下:
28、
29、进一步地,步骤s22还包括所述广义权重方程的推导:将描述固结地层中孔隙度和速度关系的双相wyllie时间平均方程拓展为三相时间平均方程,应用于天然气水合物地层中,其表达式为:
30、
31、式中,vp,t是利用wyllie方程计算的含水合物地层纵波速度;vp,m、vp,h和vp,w分别为岩石基质、水合物和水的纵波速度;
32、对所述三相时间平均方程进行改写:进一步简化为:式中,ρb为饱和岩石的体密度,ρm、ρh和ρw分别是岩石基质、水合物和水的密度;进一步,应用于天然气水合物地层的三相wood方程,其表达式为:
33、
34、式中,vp,w是wood公式计算的纵波速度;
35、对所述三相wood方程进行简化:对比简化后的三相时间平均方程和简化后的三相wood方程,引入了固结系数j,1≤j≤2,推导出所述广义权重方程,所述广义权重方程为:
36、
37、第二方面,提供一种基于双重赋存模式耦合的广义权重方程估算水合物饱和度的装置,包括:
38、初始赋值单元:确定储层的初始水合物饱和度、水合物的赋存模式、储层孔隙度、储层泥质含量;
39、所述水合物的赋存模式为双重赋存模式,所述双重赋存模式为考虑孔隙充填和骨架支撑两种微观赋存形态;
40、岩石物理模型构建单元:构建双重赋存形态水合物储层岩石物理模型;
41、目标函数设定单元:以纵波阻抗为约束构建目标函数,所述目标函数为:
42、
43、式中:和为纵波阻抗实际值和纵波阻抗预测值;ε为给定最小误差;
44、储层水合物饱和度反演单元:利用网格搜索法,基于所述目标函数进行水合物饱和度反演,估算储层水合物饱和度值。
45、进一步地,岩石物理模型构建单元中构建双重赋存形态水合物储层岩石物理模型包括:岩石基质计算单元:利用hill平均计算固体矿物与骨架支撑型水合物相结合组成的岩石基质体积模量和剪切模量,所述固体矿物包括:石英、方解石、黏土;
46、饱和岩石计算单元:利用基于双重赋存形态耦合的广义权重方程计算岩石基质与水和孔隙充填型水合物组成的饱和岩石体积模量和剪切模量。
47、进一步地,饱和岩石计算单元中利用基于双重赋存形态耦合的广义权重方程计算岩石基质与水和孔隙充填型水合物组成的饱和岩石体积模量和剪切模量,其中:
48、基于双重赋存形态耦合的广义权重方程为:
49、
50、式中:zp,w、zp,h、zp,ma和zp分别为水、水合物、岩石基质和饱和岩石的纵波阻抗;ρw、ρh、ρma和ρb分别是水、水合物、岩石基质和饱和岩石的密度,
51、ρb=(1-φ)(1-vsh)ρsd+(1-φ)vshρc+φshρh+φ(1-sh)ρw;
52、φe为有效孔隙度,φe=φ-φshfms;其中:φ、fms和sh分别为孔隙度、骨架支撑形态百分比和水合物饱和度;
53、shpfe为孔隙充填型水合物饱和度,shpfe=sh(1-fms)/[1-sh+sh(1-fms)];swe为归一化后的含水饱和度,swe=(1-sh)/[1-sh+sh(1-fms)];
54、j为水合物地层的固结系数,反映水合物地层固结程度,j越小,地层固结程度越好。进一步地,岩石基质计算单元还包括岩石基质纵波阻抗计算单元:固体矿物与骨架支撑型水合物相结合组成岩石基质,共同起到应力支撑作用,在已知各种矿物组分的体积分数和弹性模量时,利用hill平均计算岩石基质体积模量和剪切模量:
55、
56、式中,ksd、kc、kh,ms和μsd、μc、μh,ms分别为石英、黏土和骨架支撑型水合物的体积模量和剪切模量;fsd、fc和fh,ms分别为石英、黏土和骨架支撑型水合物的体积分数,其中fsd=(1-φ)(1-vsh)/(1-φ+fmsshφ),fc=(1-φ)vsh/(1-φ+fmsshφ),fh,ms=fmsshφ/(1-φ+fmsshφ),φ、vsh、fms和sh分别为孔隙度、泥质含量、骨架支撑形态百分比和水合物饱和度;
57、利用岩石物理体积模型,岩石基质密度可以表达为:
58、ρma=fsdρsd+fcρc+fh,msρh
59、式中,ρsd、ρc和ρh分别为石英、黏土和水合物的密度。
60、岩石基质纵波阻抗表达式如下:
61、
62、进一步地,饱和岩石计算单元还包括广义权重方程的推导单元:将描述固结地层中孔隙度和速度关系的双相wyllie时间平均方程拓展为三相时间平均方程,应用于天然气水合物地层中,其表达式为:
63、
64、式中,vp,t是利用wyllie方程计算的含水合物地层纵波速度;vp,m、vp,h和vp,w分别为岩石基质、水合物和水的纵波速度;
65、对所述三相时间平均方程进行改写:进一步简化为:式中,ρb为饱和岩石的体密度,ρm、ρh和ρw分别是岩石基质、水合物和水的密度;进一步,应用于天然气水合物地层的三相wood方程,其表达式为:
66、
67、式中,vp,w是wood公式计算的纵波速度;
68、对所述三相wood方程进行简化:对比简化后的三相时间平均方程和简化后的三相wood方程,引入了固结系数j,1≤j≤2,推导出所述广义权重方程,所述广义权重方程为:
69、
70、第三方面,提供一种电子设备,包括:存储器,用于存储计算机程序;处理器,用于执行所述计算机程序时实现基于双重赋存模式耦合的广义权重方程估算水合物饱和度的方法的步骤。
71、第四方面,提供一种计算机可读存储介质,所述计算机可读存储介质上存储有计算机程序,所述计算机程序被处理器执行时实现基于双重赋存模式耦合的广义权重方程估算水合物饱和度的方法的步骤。
72、通过采用上述技术方案,实现了含天然气水合物储层的水合物饱和度的定量预测。
73、与现有技术相比,本发明的有益效果是:
74、本发明基于wyllie时间平均方程和wood方程推导了广义权重方程,以此为基础,考虑孔隙充填型和骨架支撑型水合物对地层弹性响应特征的影响,进一步提出了耦合双重赋存模式的广义权重方程,并进一步结合网格搜索法发展了以纵波阻抗为约束的水合物饱和度预测方法,并应用于实际水合物地层的水合物饱和度定量预测,有效提高水合物储层建模精度和定量刻画能力。
