一种模块化获取核电站故障树顶事项失效概率的方法与流程

本发明属于故障分析技术领域，涉及一种模块化获取核电站故障树顶事项失效概率的方法。

背景技术：

故障树分析(Fault Tree Analysis,FTA)的关键是风险分析。在核行业中，故障树和事件树模型已经广泛应用于核电厂的概率安全分析，几乎所有的风险分析的研究和计算都依靠这些模型。为设计与建造那些要满足安全标准要求的系统如核电站风险监测系统等,需要在设计时就知道这些系统的安全性,及时对不满足安全性要求的系统做出合适的措施，而随着计算机技术的发展,各种控制和容错技术被广泛应用,许多系统的结构日益复杂，表现出依赖性、冗余性、可修复性、时效性等特征，这使得系统安全性的分析也越来越困难。

故障树分析是国内外核电站进行概率安全评价中广泛采用的一种建模方法。传统的故障树分析技术都是以最小割集(Minimal Cut Set，MCS)为基础的，其原理通常是首先求出网络/系统的最小割集,再按容斥定理求出顶事件概率。然而,求故障树最小割集的分析是一个存在NP困难的问题,其复杂度是底事件数量的指数倍。近年来出现的二元决策图(Binary Decision Diagram，BDD)技术是故障树分析的一种特别有效的工具，尤其是针对传统故障树分析中存在的NP问题，BDD技术显现出更为出色的运算能力。

BDD是用Boole函数表示的一种图形方式,可以直观地反映出函数的逻辑结构。它是1978年由S.B.Akers首先提出的,应用于逻辑电路的合成、模拟和测试。用BDD进行故障树分析的新思路,为核电站超大规模的系统故障树分析指明了出路和方向。近年来在核电站系统安全性分析中BDD方法日益受到重视。BDD方法可同时完成故障树的定性分析和定量分析。但在实际工程应用中,几乎不能直接使用不经过任何近似处理的BDD方法，因为从故障树转化成BDD结构的过程存在组合爆炸问题，一棵复杂故障树的BDD结构非常庞大，以至于计算机的内存无法存储，并且一个规模巨大的BDD结构的不交化割集的数量也很大，寻找出所有不交化割集和计算出结果都是非常耗时的。另外，故障树分析不仅需要尽量精确的定量分析，同时还需要定性求出MCS，显然不经近似处理求出的不交化割集不是故障树的MCS。

技术实现要素：

本发明的目的是提供一种模块化获取核电站故障树顶事项失效概率的方法。

本发明的目的是这样实现的：

本发明包括如下步骤：

(1)建立故障树：

对系统原理及故障进行分析，根据建树步骤，得出系统失效事件的故障树模型；

(2)对故障树进行模块化处理：

2.1)对故障树进行两次遍历：第一次遍历记录故障树模型中的中间事件和底事件之间的关系，遍历顺序遵循从上到下，从左到右的规则；第二次遍历按照第一次遍历相同的顺序遍历中间事件和底事件，记录每个事件的第一次访问时间T_f、第二次访问时间T_s和最后一次访问时间T_last；

2.2)计算出每个中间事件的子事件的最小访问时间Min和最大访问时间Max，通过判断区间[Min,Max]是否在区间[T_f,T_s]之间，获得故障树的模块化信息；

(3)将模块化的故障树转化为BDD结构：

“与门”计算

ite(x,G₁,G₂)ite(y,H₁,H₂)＝ite(x,G₁h,G₂h)；

“或门”计算

ite(x,G₁,G₂)+ite(y,H₁,H₂)＝ite(x,(G₁+H₁),(G₂+H₂))＝ite(x,(G₁+h),(G₂+h))；

h＝ite(y,H₁,H₂)；

式中G₁和G₂分别表示x＝0和x＝1时的布尔结构函数，H₁和H₂分别表示y＝0和y＝1时的布尔结构函数，x，y为变量，x<y；

进行吸收化简：

G＝ite(x,G₁,G₂)

H＝ite(y,H₁,H₂)

(4)对含模块的BDD结构进行遍历：

对于任意BDD结构，分别沿着根节点的左支和右支进行遍历，通过判断左支是否是终结点1，右支是否是终结点0来确定遍历是否结束，如果右支为中间节点或左支为中间节点，则以该中间节点为根节点继续遍历，直到遍历完所有路径；遍历过程中记录所有以终结点1结束的路径，依据香农原理公式对每个路径进行定量计算，最后将所有路径的概率相加得到顶事件失效概率P_top：

中，P_top表示故障树顶事件失效概率，P(C_i)表示割集C_i的概率q_k表示割集C_i中第k个事件的概率，P(C_iC_j)表示割集C_i和割集C_j同时发生的概率。

本发明的有益效果在于：本发明提出的模块化的核电站故障树顶事项失效概率的分析方法是一种低耗能、高速度的故障树分析方法，遍历经过吸收简化的最化简BDD结构，能够直接获得全部MCS并同时获得MCS的不交化割集，相比较于传统BDD方法，本发明计算效率更高、结果更为精确。模块化的BDD方法通过减小复杂故障树的规模和数量来减小计算的代价，有效降低了传统BDD方法的内存消耗，同时提高了计算效率。

附图说明

图1是本发明的求解故障树方法的流程示意图。

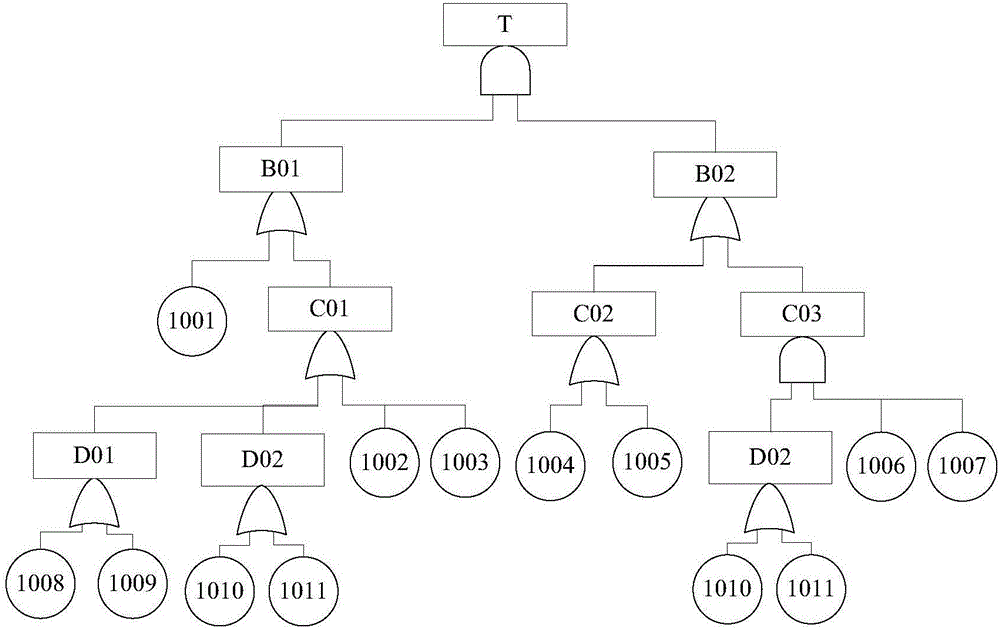
图2是本发明的方法所针对的一个故障树模型的示意图。

图3是本发明的经模块化处理后的故障子树示意图。

图4是本发明的故障子树图所对应的BDD结构示意图。

图5是本发明的模块在BDD结构中的四种情况示意图。

图6是本发明的模块化的BDD结构进行概率截断示意图。

具体实施方式

下面结合附图举例对本发明做更详细地描述：

本发明的技术方案是：一种模块化求解故障树模型的方法，图1是本发明的流程图，结合附图，具体包括如下步骤：

(1)根据需求建立故障树。

(2)对故障树进行模块化处理。故障树模块的定义为：一棵至少有两个事件的子树，并且它的底事件在故障树的其它地方不再出现。故障树模块化需要对故障树进行两次遍历。

(3)将已经模块化的故障树转化为BDD结构。将故障树转化为BDD结构之前，首先要确定底事件的排列顺序，然后按照香农原理的If-Then-Else(ITE)运算符得到相应故障树的BDD结构。

(4)对含模块的BDD结构进行遍历。BDD的遍历是指寻找BDD结构中以1为终结点的所有路径并求解顶事件失效概率的过程。由于进行吸收处理后的BDD结构都是最简化BDD结构，因此路径(不交化割集)也是故障树结构的全部MCS，所以也可以说BDD的遍历是进行故障树的定性分析和定量分析的过程。

(5)在遍历含有模块的BDD结构时加入概率截断。为了删除或避免产生对结果影响不大的MCS，常用截断手段中的概率截断来做近似处理。

(6)经过上述几个步骤得到故障树的最小割集MCS和顶事件失效概率。

(7)对模块化BDD方法进行验证。选择7颗标准故障树为对象，对比模块化BDD方法和传统BDD方法的计算结果和计算用时，可证明模块化BDD方法的计算效率要明显高于传统BDD方法。

(1)建立故障树：

对系统原理及故障进行分析，根据建树步骤，得出系统失效事件的故障树模型。如图2所示。

(2)对故障树进行模块化处理：

1)故障树模块化需要对故障树进行两次遍历：第一次遍历的目的是记录故障树模型中的中间事件和底事件之间的关系，遍历顺序遵循从上到下，从左到右的规则；第二次按照第一次遍历相同的顺序遍历中间事件和底事件，并记录他们的访问时间。

2)第一次遍历故障树结构，得到该故障树所含的中间事件和底事件，分别作为表1和表2的第一行。第二次遍历按照同样的顺序遍历，记录每个事件的第一次访问时间T_f、第二次访问时间T_s和最后一次访问时间T_last，访问结果见表1和表2。最后计算出每个中间事件的子事件的最小访问时间Min和最大访问时间Max，通过判断区间[Min,Max]是否在区间[T_f,T_s]之间，可以获得故障树的模块化信息。如表3所示。

表1中间事件访问记录

表2底事件访问记录

表3模块信息

(3)将模块化的故障树转化为BDD结构：

经过步骤(2)后，可以得到四棵故障子树，如图3所示。基于模块化的BDD方法的基本思想是把模块当成底事件来处理，并在遍历时能够识别出代表模块的底事件。在计算程序中为了方便识别、比较和计算，故障树中的中间事件与底事件都用整数来表示，按事件在故障树模块化中第一次遍历时出现的先后顺序进行依次编号，这个过程也确定底事件的排序。为了区别模块与底事件，模块用大于10000的整数来表示，编号规则为模块的顶事件编号加上10000，该值也可根据事件的数量修改。根据事件与模块的编号方法，当把模块当作底事件时，已经能够确定所有底事件的排序，因此也能够确定每棵故障子树的BDD结构。将每个模块所对应的故障子树转换成简化BDD结构可用如下公式完成。

“与门”计算

ite(x,G₁,G₂)ite(y,H₁,H₂)＝ite(x,G₁h,G₂h) (1)

“或门”计算

ite(x,G₁,G₂)+ite(y,H₁,H₂)＝ite(x,(G₁+H₁),(G₂+H₂))＝ite(x,(G₁+h),(G₂+h)) (2)

h＝ite(y,H₁,H₂) (3)

式中G₁和G₂分别表示x＝0和x＝1时的布尔结构函数，H₁和H₂分别表示y＝0和y＝1时的布尔结构函数。x，y为变量，所有公式在x<y的情况下才成立。

在求出故障树顶事件发生概率的同时希望求出MCS，因此在故障树转化成BDD结构的过程使用如下公式进行了吸收化简，从而得到最简化BDD结构，如图4所示。

G＝ite(x,G₁,G₂) (4)

H＝ite(y,H₁,H₂) (5)

(4)对含模块的BDD结构进行遍历：

传统BDD遍历方法：对于任意BDD结构，分别沿着根节点的左支和右支进行遍历，通过判断左支是否是终结点1，右支是否是终结点0来确定遍历是否结束，如果右支为中间节点或左支为中间节点，则以该中间节点为根节点继续遍历，直到遍历完所有路径。在遍历过程中需记录所有以终结点1结束的路径，依据香农原理公式对每个路径进行定量计算，最后将所有路径的概率相加得到顶事件失效概率P_top。

P_top＝ΣP(C_i)-ΣΣP(C_iC_j)+ΣΣΣP(C_iC_jC_k)-…+(-1)^N-1P(C₁C₂…C_N) (7)

式中，P_top表示故障树顶事件失效概率，P(C_i)表示割集C_i的概率q_k表示割集C_i中第k个事件的概率，P(C_iC_j)表示割集C_i和割集C_j同时发生的概率。

遍历含模块的BDD结构的基本思想是当遍历的节点为模块时，需要找到并遍历该模块所代表的BDD结构，当模块被遍历完成以后，再回到当前模块继续遍历。具体的遍历规则需要根据模块在BDD结构中所处的位置决定。当BDD结构中含有模块时，模块在BDD中出现情况可分为四种，如图5所示。以下分别介绍四类情况及其遍历规则。

1)情况1：底事件的左支和右支分别连接不同模

情况1是遍历底事件与模块相连的情况，还包括的情况有：底事件的左支与模块相连、右支与底事件或终结点相连；底事件的左支与底事件或终结点相连、右支与模块相连。由于处理这几种情况类似，因此可使用同一个遍历方法。本发明改进传统遍历的算法，在算法中添加节点的左支和右支是否是模块的判断。遍历BDD结构的每个节点时，判断该节点是底事件还是模块是通过识别节点的编号实现的。

2)情况2：模块的左支连接模块，模块的右支连接终结点0

这种情况下只考虑如何遍历这两个相联系的模块。当判断出节点为模块，并且与该节点左支相连的也是模块时，首先使用遍历函数遍历该模块所代表的BDD结构，如果遍历到模块BDD结构中的终结点1时，此时不作为路径的终点而是在路径上再次使用遍历函数遍历节点分支模块所代表的BDD结构，直到遍历完所有结构。

3)情况3：模块右支连接模块，模块左支连接终结点1

使用遍历函数Module3_Traversing(T,H)来表示，其中T为节点模块所代表的BDD结构，H为节点右支模块所代表的BDD结构。与遍历情况2时不同，在遍历T时，如果遇到终结点1则该路径即为一个MCS，当遍历完T之后再遍历H，直到遍历完所有结构。

4)情况4：模块左支与右支分别连接不同模块：

仔细观察可以发现情况4中同时含有情况2和情况3，因此在处理情况4时，只需要分别调用情况2和情况3时的遍历函数即可完成遍历。

(5)基于模块化的BDD方法的截断:

不管是传统BDD方法还是模块化的BDD方法，都能得到故障树的全部MCS，但是在定量化计算中大部分的MCS对结果几乎没有影响，因此没有必要获得故障树的全部MCS。为了删除或避免产生对结果影响不大的MCS，常用截断手段中的概率截断来做近似处理。

传统BDD方法中的概率截断原理为：在BDD结构遍历过程中，当遍历到某个节点时，如 果此时路径的概率值小于设定的截断值，就把以该节点为根节点的BDD结构当作终结点0。基于模块化的BDD方法的截断与传统BDD方法没有差别，只是在截断时会产生更好的效果，比如由于截断使得有些模块所代表的BDD结构至始至终都没有被遍历，因此即使不产生这些模块的BDD结构也能完成计算，从而提高计算效率。

在遍历图6所示的含模块的BDD结构时使用概率截断，如果底事件的概率都为0.1、概率截断值为0.01。当遍历到节点1003和节点1005时，路径的概率为0.009小于概率截断值，按照截断的遍历规则分别将以这两个节点为根节点的BDD结构当作终结点0。将图6中的两个虚线内的BDD结构替换成终结点0后的结构，可简化为BDD结构。由于遍历过程没有遍历到模块10001和10002，因此模块10001和10002所代表的故障子树可以不需要转化成BDD结构。截断后的故障树为图6所示。

(6)经过上述几个步骤得到故障树的最小割集MCS和顶事件失效概率P_top。

(7)对模块BDD方法进行验证：

为了验证模块化BDD方法的正确性和高效性，选择了7颗标准故障树为对象，对比基于模块化的BDD方法和传统BDD方法的计算结果和计算用时,结果如表4所示。

表4模块化的BDD方法和传统BDD方法的计算结果

通过对比模块化的BDD方法和传统BDD方法的计算结果可以发现：

1)选择的7颗故障树中除了传统BDD方法不能计算Isp9604和edf9201外，得到的MCS数量是一样的，可证明基于模块化的BDD方法的逻辑运算是正确的，能够计算出故障树的全部MCS；

2)能计算的5颗故障树中，除了没有模块的Chinese外，模块化的BDD方法所需要的计算时间更短，可证明模块化的BDD方法的计算效率要明显高于传统的BDD方法；

3)传统BDD方法在故障树Isp9604和edf9201时会发生内存溢出而无法计算出结果，而模块化的BDD方法能够在较短时间内完成计算并得到结果，可说明模块化的BDD结构提高了BDD处理复杂故障树的能力。

本发明具有如下优点：本发明提出的模块化求解故障树模型的方法是一种低耗能，高速度的故障树分析方法，遍历经过吸收简化的最化简BDD结构，能够直接获得全部MCS并同时获得MCS的不交化割集，相比较于传统BDD方法，本发明计算效率更高，结果更为精确。模块化的BDD方法通过减小复杂故障树的规模和数量来减小计算的代价。在传统BDD遍历方法的基础上修改和添加规则。最后，对复杂的故障树还需要使用截断手段来提高计算速度以满足核电站的要求。

以上所述仅为本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。