一种在轨服务机械臂动力学建模方法和系统与流程

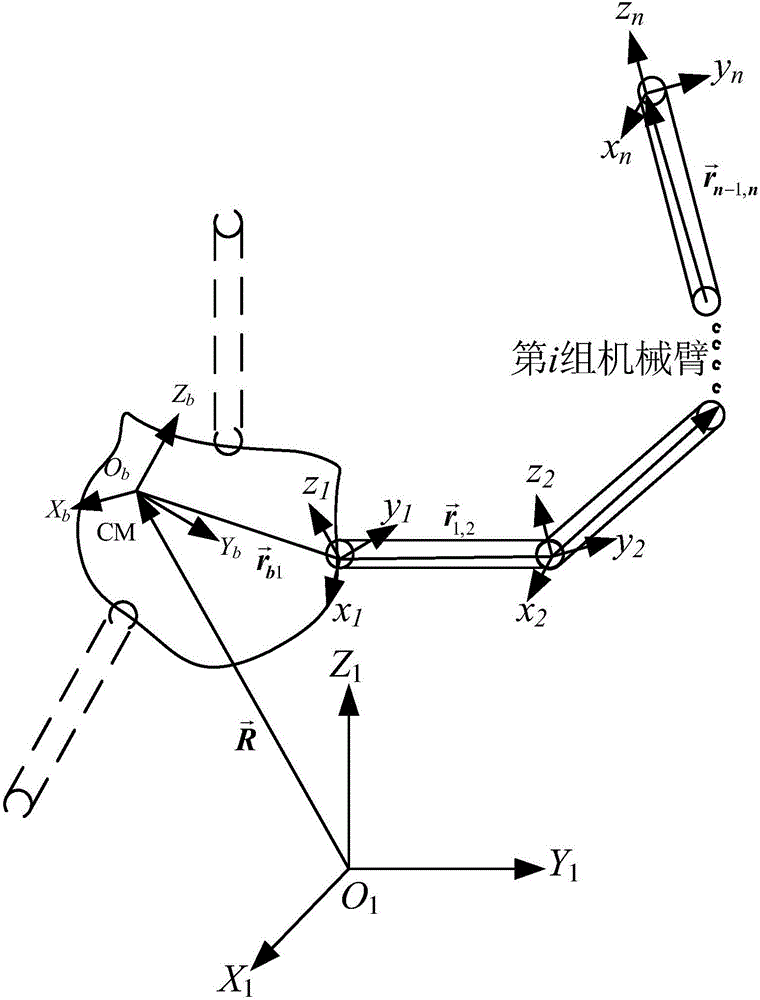
本发明涉及一种多自由度系统的动力学建模方法，具体涉及一种基于凯恩方程在轨服务多臂多自由度机械臂系统的动力学建模方法和系统。
背景技术：
：随着空间技术的进步，全球每年发射的卫星和航天器的数量在不断增加，随之而来的是空间工作的多样性和复杂性迅速增长，对舱外活动的需求也日益增加，如对在轨航天器的抓捕、维修和燃料补充，外空间环境的科学实验，对空间垃圾的清理等等。过去这些任务主要由宇航员完成，但这些活动受到很多限制：首先，宇航员的力量与工作范围有限，对于大尺寸的航天设备的安装无能为力；其次，由于氧气供应和外太空辐射等含有危险的原因，宇航员的舱外连续工作时间有限；另外，由于太空微重力、高真空、强辐射和微小行星体的存在，在太空环境下从事各种作业，对宇航员来说是十分困难和危险的；同时为支持宇航员的舱外活动，需要庞大而复杂的环境控制系统和生命保障系统，不可避免的带来巨大的费用支出。为了解决这些问题，在轨服务机械臂系统应运而生。而一种好的在轨服务机械臂动力学建模方法是机械臂结束的核心技术之一。本质上，所有动力学建模的方法都是等效的。然而，不同的方法的使用难易程度是不同的。目前，多体系统动力学建模的主要方法有3种，即牛顿－欧拉方法、Lagrange方法和Kane方法。牛顿－欧拉方法基本上能解决全部的多体动力学建模问题，但是计算效率很低。牛顿－欧拉方法需要考虑多体系统的每个个体所受到的力和力矩之间的平衡关系，其中包括各个个体之间的相互关联的力和约束力，所以它的效率很低。Lagrange方法不需要虑多体系统的各个个体之间的相互关联的力和约束力，但是它最大的缺点是需要对能量函数进行微分。对于自由度较少的多体系统，计算量不算大，但是对于自由度较多的多体系统，它的计算量和计算效率是一个不容忽略的问题。相对于牛顿－欧拉方法和Lagrange方法，Kane方法具有它们所没有的优势。因为Kane方法采用广义力的概念，所以可以忽略多体系统的各个个体之间的相互关联的力和约束力。因为Kane方法没有使用能量方程，所以对方程的微分对计算量的影响不大。因此，针对在轨服务机械臂系统的计算量比牛顿－欧拉方法和Lagrange方法要小的多。使用Kane方法能大大提高计算效率，缩短计算时间。技术实现要素：本发明提供一种在轨服务机械臂动力学建模方法，具有系统模型计算量小的特点，达到系统运行实时性的目的。为实现上述目的，本发明提供一种在轨服务机械臂动力学建模方法，其特点是，该方法包含：S1、定义机械臂系统的系统坐标系，以及矢量参数和速度参数；S2、确定系统的广义偏速度，并得出该广义偏速度对应的广义惯性力和广义主动力；S3、广义主动力和广义惯性力带入凯恩方程，得到机械臂系统中所有节臂的动力学方程；S4、机械臂系统中所有节臂的动力学方程进行简化，合并成整个机械臂系统的动力学模型。上述定义机械臂系统的系统坐标系包含：惯性坐标系SI：原点OI位于地球中心，ZI轴沿地球指向北极，XI轴指向春分点，YI轴满足右手定则；轨道坐标系So：原点Oo位于系统质心，zo轴指向地心，yo轴指向轨道负法线方向，xo轴与其它两轴构成右手坐标系；中心体连体坐标系Sb：原点Ob位于复杂连接体中心体的质心，xb、yb和zb与中心体惯性主轴平行，且满足右手定则；当中心体相对于轨道坐标系的三个方位角为零时，Sb坐标系与So系一致；机械臂坐标系Sji(i＝1，2，…M；j＝1，2，…Ni)：设系统有i个机械臂，对应第i个机械臂有Ni节，定义第i个机械臂中第j节臂的机械臂坐标系为：原点位于第i个机械臂系统中的第j节机械臂与其内接体的铰链oji处，坐标系各轴与第j节机械臂固连。上述定义矢量参数包含：中心体连体坐标系原点在惯性坐标系中的位置矢量中心体质心在中心体连体坐标系内的位置矢量中心体质心在惯性坐标系内的位置矢量第i组机械臂中第一节机械臂在中心体上的铰接点在中心体连体坐标系中的位置矢量第i组机械臂中第j(j＝2,3,…,Ni)节机械臂与第j-1节机械臂的连接点在第j-1节机械臂的连体坐标系中的位置矢量第i组机械臂中第j节机械臂的质心在其自身连体坐标系中的位置矢量第i组机械臂中第j节机械臂的质心在惯性坐标系中的位置矢量上述定义速度参数包含：中心体连体系相对惯性系的角速度矢量第i组机械臂中第j节机械臂相对其自身连体坐标系的角速度矢量第i组机械臂中第j节机械臂相对惯性坐标系的角速度矢量上述S2包含：分析机械臂系统，选定广义偏速度；根据广义偏速度，计算出该广义偏速度下的广义惯性力和广义主动力；广义惯性力包含：中心体惯性力和第i组机械臂第j节臂的惯性力。上述中心体惯性力包含：中心体第k(k>2)阶广义惯性力如式(1)：fIk,B*=-∫B(a→B·G→k,B)dm=0,k>2---(1)]]>其中，为B体的绝对加速度，为第k阶广义偏速度；上述第i组机械臂第j节臂的惯性力包含：第i组机械臂第j节臂的第2+N*(i-1)+l阶广义惯性力如式(2)：fIn,j*i=-∫i,j(a→ji·G→n,ji)dm=-∫i,j(r~l,jiT+Alji1r~jiTAjli)eliT·eITR··-ebT(r~b,ji+Abjir~jiAjbi)ω·b-Σk=1jekiT(r~k,ji+Akjir~jiAjki)ω·ki-ebTω~br~b,1iωb-Σk=1j-1ekiTΩ~kir~k,k+1iΩki-ejiTΩ~jir~jiΩji-e1iT(r~1,ji+A1jir~jiAj1i)A1biω~bAb1iΩ1i-Σk=2jekiT(r~k,ji+Akjir~jiAjki)Ak,k-1iΩ~k-1iAk-1,kiΩkidm(n=2+N*(i-1)+l,l≤j)---(2)]]>其中，为第j节臂绝对加速度，为j节机械臂上第n阶广义偏速度，上式中所有e都为连体基，其下标表示为在哪个坐标系下，上标表示为第几组，T表示转置；A表示方向余弦矩阵，下标表示为后者对前者的方向余弦矩阵，上标表示在哪个坐标系下；表示位置的叉乘矩阵，下标为后一点相对前一点，上标为在哪个坐标系下；ω表示角速度，下标表示是那个体；Ω为关节旋转角速度，下标表示哪个体，上标表示相对那个坐标系。上述S3包含：把广义主动力和广义惯性力带入凯恩方程，得到N*M+2个力学平衡方程，包含：中心体平动方程、中心体转动方程和第i组机械臂第j节臂的转动方程(i＝1，2，…M；j＝1，2，…N)：中心体平动方程包含：中心体平动方程对应于第一阶广义速度如式(3)：mR··-AIbS~otω·b-Σi=13Σj=17AIjiS~jtiω·ji-AIbω~bS~b*ωb-Σi=13Σj=17AIjiΩ~jiS~ji*Ωji-Σi=13(AI1iS~1tiA1biω~bAb1iΩ1i+Σj=27AIjiS~jtiAj,j-1iΩ~j-1iAj-1,jiΩji)=F---(3);]]>中心体转动方程包含：中心体转动方程对应于第二阶广义速度ωb，如式(4)：-S~otTAbIR··+Iotω·b+Σi=13Σj=17AbjiIj_oiω·ji+Iωωb+Σi=13Σj=17AbjiIΩj_oiΩji+Σi=13(Ab1iI1_oiA1biω~bAb1iΩ1i+Σj=27AbjiIj_oiAj,j-1iΩ~j-1iAj-1,jiΩji)=T---(4);]]>第i组机械臂第N节臂的转动方程包含：第i组机械臂第N节臂的转动方程对应于第(2+N*(i-1)+N)阶广义速度如式(5)-S~NtiTANIiR··+IN_oiTANbiω·b+Σj=1N-1IN_jiTANjiω·ji+INtiω·Ni+S~NtiTANbiω~br~b,1iωb+Σj=1N-1ANjiIΩj_NiΩji+IΩNiΩNi+IN_1iTANbiω~bAb1iΩ1i+Σj=2N-1IN_jiTAN,j-1iΩ~j-1iAj-1,jiΩji+INtiAN(N-1)iΩ~(N-1)iA(N-1)NiΩNi=TNi---(5).]]>上述S4中，经整理后的机械臂系统的动力学方程如式(6)：M~Y·~=Q~-Q~N---(6)]]>式中为系统的质量阵，表达式如式(7)：M~=mE3-AIbS~t-AI11S1t1...-AI71SNt1-AI12S1t2...-AIN2SNt2...-AI1MS1tM...-AINMS7NMItAb11I1_o1...AbN1IN_o1Ab12I1_o2...AbN2IN_o2...Ab1MI1_oM...AbNMIN_oMI1t1...A1N1IN_110000........................INt10000I1t2...A1N2IN_1200........................INt200I1tn...A1NMIN_1M........................INtM---(7)]]>质量阵为对称正定阵，因此只给出了对角线及以上的元素；为系统的广义速度列阵，表达式如式(8)：Y~=R·TωbTω11T...ωN1Tω12T...ωN2T...ω1MT...ωNMTT---(8)]]>为广义力列阵，表达式如式(9)：Q~=FTTTT11T...TN1TT12T...TN2T...T1MT...TNMTT---(9).]]>上述建模方法用于航天器本体及搭载在航天器本体上的N个多自由度机械臂的联合机械臂系统的动力学建模。一种在轨服务机械臂动力学建模系统，其特点是，该系统包含：坐标系定义模块，其定义机械臂系统的系统坐标系，以及矢量参数和速度参数；广义惯性力和广义主动力计算模块，其接收系统坐标系、矢量参数和速度参数，确定系统的广义偏速度，并得出该广义偏速度对应的广义惯性力和广义主动力；动力学方程建立模块，其接收广义惯性力和广义主动力计算模块带入凯恩方程，得到机械臂系统中所有节臂的动力学方程；动力学模型建立模块，其接收机械臂系统中所有节臂的动力学方程并进行简化，合并成整个机械臂系统的动力学模型。本发明一种在轨服务机械臂动力学建模方法和系统和现有技术相比，其优点在于，本发明只需要获得广义主动力和广义惯性力，不需要考虑个物体之间的约束力，也不需要计算系统的动能和势能，所以该方法非常简便，克服了其它建模方法计算量大、物理意义不直观、建模复杂度高的缺点。附图说明图1为本发明一种在轨服务机械臂动力学建模方法的流程图；图2为在轨服务机械臂系统的构型图。具体实施方式以下结合附图，进一步说明本发明的具体实施例。如图1所示，本发明公开了一种采用凯恩原理在轨服务机械臂动力学建模方法，该方法以航天器本体及搭载在航天器本体上的N个多自由度机械臂的联合机械臂系统动力学建模的前提条件为基础，该方法具体包含以下步骤：S1、如图2所示，定义机械臂系统的系统坐标系，以及矢量参数和速度参数。系统坐标系包含：惯性坐标系SI(OIXIYIZI)：原点OI位于地球中心，ZI轴沿地球指向北极，XI轴指向春分点，YI轴满足右手定则。轨道坐标系So(Ooxoyozo)：原点Oo位于系统质心，zo轴指向地心，yo轴指向轨道负法线方向，xo轴与其它两轴构成右手坐标系。中心体连体坐标系Sb(Obxbybzb)：原点Ob位于复杂连接体中心体的质心，xb、yb和zb与中心体惯性主轴平行，且满足右手定则；当中心体相对于轨道坐标系的三个方位角为零时，Sb坐标系与So系一致。机械臂坐标系Sji(ojixjiyjizji)((i＝1，2，…M；j＝1，2，…Ni)：设系统有i个机械臂，对应第i个机械臂有Ni节，定义第i个机械臂中第j节臂的机械臂坐标系为：原点位于第i个机械臂系统中的第j节机械臂与其内接体的铰链oji处，坐标系各轴与第j节机械臂固连。定义的矢量参数包含：中心体连体坐标系原点在惯性坐标系中的位置矢量中心体质心在中心体连体坐标系内的位置矢量中心体质心在惯性坐标系内的位置矢量第i组机械臂中第一节机械臂在中心体上的铰接点在中心体连体坐标系中的位置矢量第i组机械臂中第j(j＝2,3,…,Ni)节机械臂与第j-1节机械臂的连接点在第j-1节机械臂的连体坐标系中的位置矢量第i组机械臂中第j节机械臂的质心在其自身连体坐标系中的位置矢量第i组机械臂中第j节机械臂的质心在惯性坐标系中的位置矢量定义的速度参数包含：中心体连体系相对惯性系的角速度矢量第i组机械臂中第j节机械臂相对其自身连体坐标系的角速度矢量第i组机械臂中第j节机械臂相对惯性坐标系的角速度矢量S2、选择系统广义偏速度，并计算出所选择的偏速度下对应的广义主动力和广义惯性力。首先，对系统进行分析，选择适当的广义偏速度。偏速度包括：中心体偏速度向量和各个机械臂各节臂的的偏速度向量。然后，根据所选择的广义偏速度，计算出所选择的偏速度下对应的广义主动力和广义惯性力。S2.1、选择广义偏速度：表1、中心体偏速度向量表2第i组机械臂第j节臂的偏速度向量S2.2、计算广义惯性力。1)中心体惯性力：a)中心体第1阶广义惯性力如下：fI1,B*=-∫B(a→B·G→1,B)dm=-∫BE3eI[eITR··-ebTω~br~bωb-ebTr~bω·b]dm=-∫B[R··-AIbω~br~bωb-AIbr~bω·b]dm=-mBR··+AIbω~bS~bωb+AIbS~bω·b]]>其中：Sb＝∫Brbdm。b)中心体第2阶广义惯性力如下：fI2,B*=-∫B(a→B·G→2,B)dm=-∫B-r~bTeb·[eITR··-ebTω~br~bωb-ebTr~bω·b]dm=∫Br~bT[AIbR··-ω~br~bωb-r~bω·b]dm=S~bTAIbR··-Jωbωb-Jbω·b]]>其中：c)中心体第k(k>2)阶广义惯性力如式(1)：fIk,B*=-∫B(a→B·G→k,B)dm=0,k>2---(1)]]>其中，为B体的绝对加速度，为第k阶广义偏速度。2)第i组机械臂第j节臂的惯性力：a)第i组机械臂第j节臂的第1阶广义惯性力如下：fI1,j*i=-∫i,j(a→ji·G→1,ji)dm=-mjiR··-AIb(mjir~b,ji+AbjiS~jiAjbi)ω·b-Σk=1jAIki(mjir~k,ji+AkjiS~jiAjki)ω·ki-mjiAIbω~br~b,1iωb-Σk=1j-1mjiAIkiΩ~kir~k,k+1iΩki-AIjiΩ~jiS~jiΩji-AI1i(mjir~1,ji+A1jiS~jiAj1i)A1biω~bAb1iΩ1i-Σk=2jAIki(mjir~k,ji+AkjiS~jiAjki)Ak,k-1iΩ~k-1iAk-1,kiΩki]]>第i组机械臂第j节臂的第2阶广义惯性力如下：fI2,j*i=-∫i,j(a→ji·G→2,ji)dm=-∫i,j(r~b,jiT+Abjir~jiTAjbi)·AbIR··-(r~b,ji+Abjir~jiAjbi)ω·b-Σk=1jAbki(r~k,ji+Akjir~jiAjki)ω·ki-ω~br~b,1iωb-Σk=1j-1AbkiΩ~kir~k,k+1iΩki-AbjiΩ~jir~jiΩji-Ab1i(r~1,ji+A1jir~jiAj1i)A1biω~bAb1iΩ1i-Σk=2jAbki(r~k,ji+Akjir~jiAjki)Ak,k-1iΩ~k-1iAk-1,kiΩkidm]]>第i组机械臂第j节臂的第2+N*(i-1)+l阶广义惯性力如式(2)：fIn,j*i=-∫i,j(a→ji·G→n,ji)dm=-∫i,j(r~l,jiT+Alji1r~jiTAjli)eliT·eITR··-ebT(r~b,ji+Abjir~jiAjbi)ω·b-Σk=1jekiT(r~k,ji+Akjir~jiAjki)ω·ki-ebTω~br~b,1iωb-Σk=1j-1ekiTΩ~kir~k,k+1iΩki-ejiTΩ~jir~jiΩji-e1iT(r~1,ji+A1jir~jiAj1i)A1biω~bAb1iΩ1i-Σk=2jekiT(r~k,ji+Akjir~jiAjki)Ak,k-1iΩ~k-1iAk-1,kiΩkidm(n=2+N*(i-1)+l,l≤j)---(2)]]>其中，为第j节臂绝对加速度，为j节机械臂上第n阶广义偏速度，上式中所有e都为连体基，其下标表示为在哪个坐标系下，上标表示为第几组，T表示转置；A表示方向余弦矩阵，下标表示为后者对前者的方向余弦矩阵，上标表示在哪个坐标系下；表示位置的叉乘矩阵，下标为后一点相对前一点，上标为在哪个坐标系下；ω表示角速度，下标表示是那个体；Ω为关节旋转角速度，下标表示哪个体，上标表示相对那个坐标系。S2.3、计算系统广义主动力，如表3。表3广义主动力S3、把广义主动力和广义惯性力带入凯恩方程，得到机械臂系统中所有节臂的动力学方程，具体得到N*M+2个力学平衡方程，包含：中心体平动方程、中心体转动方程和第i组机械臂第j节臂的转动方程(i＝1，2，…M；j＝1，2，…N)。1)中心体平动方程包含：中心体平动方程对应于第一阶广义速度如式(3)：mR··-AIbS~otω·b-Σi=13Σj=17AIjiS~jtiω·ji-AIbω~bS~b*ωb-Σi=13Σj=17AIjiΩ~jiS~ji*Ωji-Σi=13(AI1iS~1tiA1biω~bAb1iΩ1i+Σj=27AIjiS~jtiAj,j-1iΩ~j-1iAj-1,jiΩji)=F---(3);]]>2)中心体转动方程包含：中心体转动方程对应于第二阶广义速度ωb，如式(4)：-S~otTAbIR··+Iotω·b+Σi=13Σj=17AbjiIj_oiω·ji+Iωωb+Σi=13Σj=17AbjiIΩj_oiΩji+Σi=13(Ab1iI1_oiA1biω~bAb1iΩ1i+Σj=27AbjiIj_oiAj,j-1iΩ~j-1iAj-1,jiΩji)=T---(4);]]>3)第i组机械臂第1节臂的转动方程包含：第i组机械臂第1节臂的转动方程对应于第(2+N*(i-1)+1)阶广义速度因此有：-S~1tiTA1IiR··+I1_oiTA1biω·b+I1tiω·1i+Σj=27A1jiIj_1iω·ji+S~1tiTA1biω~br~b,1iωb+IΩ1iΩ1i+Σj=27A1jiIΩj_1iΩji+I1tiA1biω~bAb1iΩ1i+Σj=27A1jiIj_1iAj,j-1iΩ~j-1iAj-1,jiΩji=T1i;]]>4)第i组机械臂第2节臂的转动方程包含：第i组机械臂第2节臂的转动方程对应于第(2+N*(i-1)+2)阶广义速度因此有：-S~2tiTA2IiR··+I2_oiTA2biω·b+I2_1iTA21iω·1i+I2tiω·2i+Σj=37A2jiIj_2iω·ji+S~2tiTA2biω~br~b,2iωb+A21iIΩ1_2iΩ1i+IΩ2iΩ2i+Σj=37A2jiIΩj_2iΩji+I2_1iTA2biω~bAb,1iΩ1i+I2tiA21iΩ~1iA12iΩ2i+Σj=37A2jiIj_2iAj,j-1iΩ~j-1iAj-1,jiΩji=T2i;]]>5)第i组机械臂第3节臂的转动方程包含第i组机械臂第3节臂的转动方程对应于第(2+N*(i-1)+3)阶广义速度因此有：-S~3tiTA3IiR··+I3_oiTA3biω·b+Σj=12I3_jiTA3jiω·ji+I3tiω·3i+Σj=47A3jiIj_3iω·ji+S~3tiTA3biω~br~b,1iωb+Σj=12A3jiIΩj_3iΩji+IΩ3iΩ3i+Σj=47A3jiIΩj_3iΩji+I3_1iTA3biω~bAb1iΩ1i+I3_2iTA31iΩ~1iA12iΩ2i+I3tiA32iΩ~2iA23iΩ3i+Σj=47A3jiIj_3iAj,j-1iΩ~j-1iAj-1,jiΩji=T3i............;]]>6)第i组机械臂第N-1节臂的转动方程包含：第i组机械臂第N-1节臂的转动方程对应于第(2+N*(i-1)+N-1)阶广义速度因此有：-S~(N-1)tiTA(N-1)IiR··+I(N-1)_oiTA(N-1)biω·b+Σj=1N-2I(N-1)_jiTA(N-1)jiω·ji+I(N-1)tiω·(N-1)i+A(N-1)NiIN_(N-1)iω·Ni+S~(N-1)tiTA(N-1)biω~br~b,1iωb+Σj=1N-2A(N-1)jiIΩj_(N-1)iΩji+IΩ(N-1)iΩ(N-1)i+A(N-1)NiIΩN_(N-1)iΩ(N-1)i+I(N-1)_1iTA(N-1)biω~bAb1iΩ1i+Σj=2N-2I(N-1)_jiTA(N-1),j-1iΩ~j-1iAj-1,jiΩji+I(N-1)tiA(N-1)(N-2)iΩ~(N-2)iA(N-2)(N-1)iΩ(N-1)i+A(N-1)NiIN_(N-1)iAN(N-1)iΩ~(N-1)iA(N-1)NiΩNi=T(N-1)i;]]>7)第i组机械臂第N节臂的转动方程包含：第i组机械臂第N节臂的转动方程对应于第(2+N*(i-1)+N)阶广义速度如式(5)-S~NtiTANIiR··+IN_oiTANbiω·b+Σj=1N-1IN_jiTANjiω·ji+INtiω·Ni+S~NtiTANbiω~br~b,1iωb+Σj=1N-1ANjiIΩj_NiΩji+IΩNiΩNi+IN_1iTANbiω~bAb1iΩ1i+Σj=2N-1IN_jiTAN,j-1iΩ~j-1iAj-1,jiΩji+INtiAN(N-1)iΩ~(N-1)iA(N-1)NiΩNi=TNi---(5)]]>S4、机械臂系统中所有节臂的动力学方程进行简化，合并成整个机械臂系统的动力学模型。对S3计算得到的方程，经整理后的机械臂系统的动力学方程如式(6)：M~Y·~=Q~-Q~N---(6);]]>式中为系统的质量阵，表达式如式(7)：M~=mE3-AIbS~t-AI11S1t1...-AI71SNt1-AI12S1t2...-AIN2SNt2...-AI1MS1tM...-AINMS7NMItAb11I1_o1...AbN1IN_o1Ab12I1_o2...AbN2IN_o2...Ab1MI1_oM...AbNMIN_oMI1t1...A1N1IN_110000........................INt10000I1t2...A1N2IN_1200........................INt200I1tn...A1NMIN_1M........................INtM---(7)]]>质量阵为对称正定阵，因此只给出了对角线及以上的元素；为系统的广义速度列阵，表达式如式(8)：Y~=R·TωbTω11T...ωN1Tω12T...ωN2T...ω1MT...ωNMTT---(8);]]>为广义力列阵，表达式如式(9)：Q~=FTTTT11T...TN1TT12T...TN2T...T1MT...TNMTT---(9);]]>为非线性项列阵，为高阶小量，可忽略。本发明还公开了一种在轨服务机械臂动力学建模系统，该系统包含：坐标系定义模块、连接坐标系定义模块的广义惯性力和广义主动力计算模块、连接广义惯性力和广义主动力计算模块的动力学方程建立模块、连接动力学方程建立模块的动力学模型建立模块。坐标系定义模块用于定义机械臂系统的系统坐标系，以及矢量参数和速度参数。广义惯性力和广义主动力计算模块接收系统坐标系、矢量参数和速度参数，用于确定系统的广义偏速度，并得出该广义偏速度对应的广义惯性力和广义主动力；动力学方程建立模块接收广义惯性力和广义主动力计算模块带入凯恩方程，得到机械臂系统中所有节臂的动力学方程。动力学模型建立模块接收机械臂系统中所有节臂的动力学方程并进行简化，合并成整个机械臂系统的动力学模型。尽管本发明的内容已经通过上述优选实施例作了详细介绍，但应当认识到上述的描述不应被认为是对本发明的限制。在本领域技术人员阅读了上述内容后，对于本发明的多种修改和替代都将是显而易见的。因此，本发明的保护范围应由所附的权利要求来限定。当前第1页1 2 3