基于模糊控制器的升力式再入预测-校正制导方法与流程

本发明涉及制导控制技术领域,特别是一种基于模糊控制器的可重复使用飞行器再入预测-校正制导方法。

背景技术：

可重复使用飞行器(Reusable Launch Vehicle，RLV)是指能够自由往返于太空与地球之间、多次重复发射、实现水平定点着降的飞行器。可重复使用飞行器具有大升阻比外形(升阻比一般大于0.5)，机动能力较强。美国在RLV方面的研究开展得较早，一直处于世界领先的位置。第一代RLV飞行器以航天飞机为代表，它的诞生使得航天器的可重复使用由理想变为现实，具有历程碑意义。第二代RLV研制的主要型号有X-33先进技术验证机、X-34小型亚轨道飞行验证机、X-37二级入轨验证机和X-37B轨道试验飞行器。X-37B项目的成功体现了美国在RLV技术上的巨大优势，及未来空天飞行器的发展方向。目前，美国正在着力开展第三代RLV的研制，致力提高RLV飞行器的安全性和可靠性。计划到2040年，美国第四代RLV可以在地球任何一个地区起飞，通过多种方式进入轨道，并能够返回再入到达任何预定的目的地。近些年来，我国在该方面也进行了大量的研究，并进行了相关实验，国产可重复使用飞行器投入实践有日可待。

可重复使用飞行器返回再入过程分为四个阶段，即离轨段、再入段、末端能量管理段(TAEM)和着陆段。其中，再入段是最复杂、难度最大的阶段。在该阶段，飞行器从二十多马赫的速度降到2～3马赫，需要满足热流、过载、动压等过程约束，以及能量、位置、航向角等终端约束。

可重复使用飞行器再入制导方法可分为两类：一类是标准轨迹制导，另一类是预测-校正制导。标准轨迹制导法包含离线标准轨迹设计和在线轨迹跟踪两部分，已在航天飞机上成功应用。该方法首先在飞行走廊内设计阻力加速度-速度(D-V)剖面，然后设计轨迹跟踪控制器，跟踪D-V剖面。为了适应新一代RLV再入制导需要，航天飞机再入制导方法得到了进一步发展，主要体现在飞行剖面优化与设计、跟踪控制规律设计方法、剖面更新技术等方面。比如演化加速度再入制导方法(Evolved Acceleration Guidance Logic for Entry,EAGLE)。EAGLE最突出特性在于能够规划三维轨迹，从而具备处理大侧向机动问题的能力。

标准轨迹制导方法虽然在实际应用中取得了巨大成功，但其主要缺陷在于无法摆脱对标准轨迹的依赖，灵活性不足。因此，近些年来人们把目光投向预测-校正制导方法。预测-校正制导方法包含轨迹预测和指令校正两部分。根据预测方式不同，预测-校正制导可以分为解析预测-校正制导和数值预测-校正制导。解析预测-校正制导通过近似的解析公式预测轨迹，计算量很小，能够满足在线计算的要求，但制导精度较低，对过程约束处理不好。数值预测-校正制导利用运动方程的数值积分对轨迹进行预测，预测精度较高，但计算量很大，不利于工程实现。随着计算机水平的提高,数值预测制导正受到越来越多的关注。

技术实现要素：

本发明所要解决的技术问题是，针对现有技术不足，提供一种基于模糊控制器的可重复使用飞行器再入预测-校正制导方法。

为解决上述技术问题，本发明所采用的技术方案是：一种基于模糊控制器的可重复使用飞行器再入预测-校正制导方法，该方法为：一种基于模糊控制器的可重复使用飞行器再入预测-校正制导方法，该方法为：

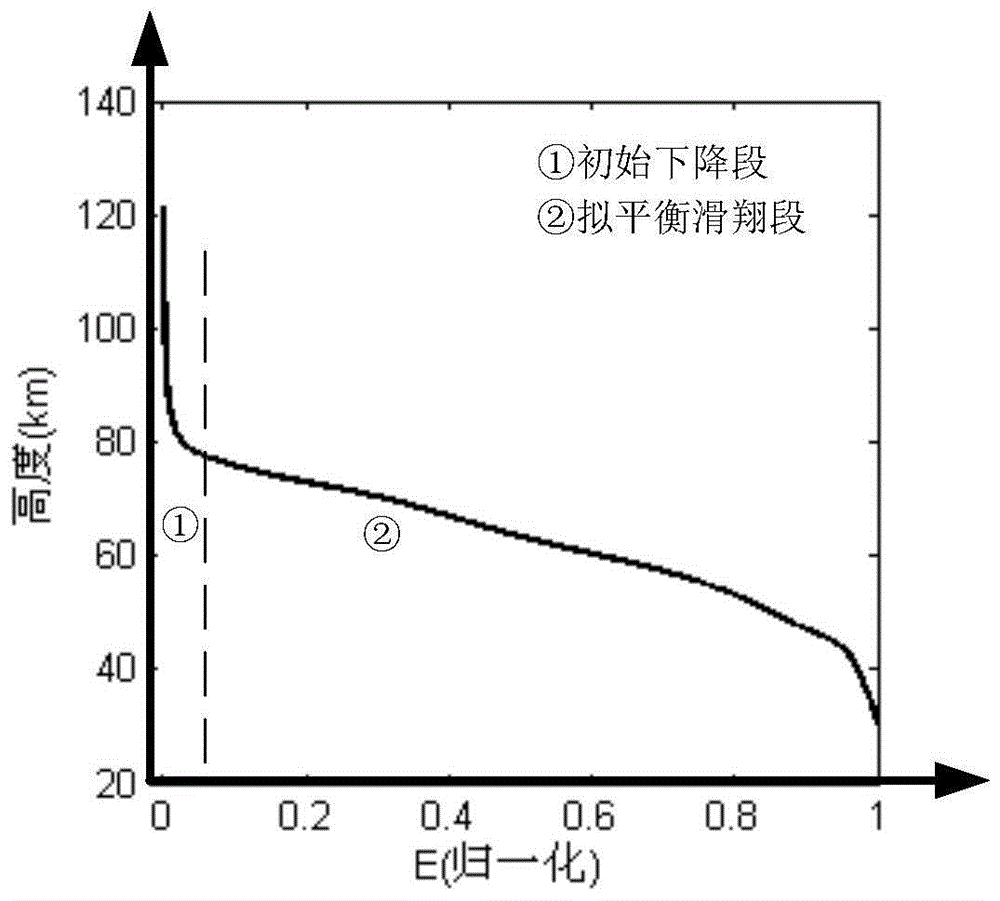
1)飞行器再入开始时，根据状态偏差、气动系数偏差计算初始下降段的倾侧角大小|σini|，同时根据飞行器到目标点的视线角计算倾侧角的符号sign(σini)，在σini的制导作用下，飞行器不断下降，直到满足初始下降段的结束条件

其中，δ为进入平衡滑翔状态的门限值，可设置为0.02，r为地心距，V为飞行器的速度，地心距对速度求导dr/dV＝-Vsinθ/(D+gsinθ)，θ为速度倾角，D为阻力加速度，g为重力加速度，(dr/dV)QEGC为平衡滑翔弹道在高度-速度剖面对应的斜率，通过对平衡滑翔条件求关于V的微分得到；

2)进入滑翔段后，根据当前状态和加速度计的测量结果，更新大气密度和气动系数误差模型，确保这些模型与实际相符；

3)以当前点为起始点进行轨迹预测，首先建立攻角和倾侧角剖面的模型，然后采用龙哥库塔数值积分方法，以能量为自变量，对再入动力学模型进行数值积分，当飞行器的能量达到截止条件时，结束积分，得到终端状态，并计算航程偏差ΔR，高度偏差Δh、以及横向位置偏差CR；

4)根据预测的终端航向角更新再入终端位置，即进入TAEM区域的入口，确保飞行器垂直进入TAEM区域，

其中，λT和φT为着陆场的经纬度，λF和φF为TAEM区域入口的经纬度，RTAEM为TAEM区域的半径，ψ为飞行方位角；

5)根据预测结果校正制导指令，采用两个模糊控制器进行校正，模糊控制器A的输入为剩余能量Eto-go、航程偏差ΔR，输出为倾侧角校正量Δσ和攻角校正量Δα，模糊控制器B的输入为横向位置偏差CR，输出为倾侧角翻转时机的变化量ΔE；

6)得到倾侧角校正量Δσ后，对Δσ进一步处理，从而完成对当前倾侧角的校正，

|σc|＝|σc|pre+kσΔtsim

其中，Δtgud为制导周期，kσ为倾侧角变化的斜率，Δtsim为仿真积分步长，|σc|pre为上一制导周期的倾侧角，|σc|为当前的倾侧角；

7)计算经步骤6)校正后的倾侧角的约束边界，如果倾侧角的幅值超出边界，则取边界值

其中，为热流约束对倾侧角的限制，σq,max为动压约束对倾侧角的限制，σn,max为过载约束对倾侧角的限制，kmax设计为常值或者分段线性函数，针对不同的飞行器kmax的取值不同(比如取常值0.95)，kmax起到修正倾侧角边界的作用；

8)在校正当前倾侧角时，同时对倾侧角剖面模型的节点进行调整，即改变轨迹预测的倾侧角剖面模型：

|σm|＝|σm|pre+kmΔσ

其中，km为0～1的可调常数，|σm|为倾侧角模型的节点，|σm|pre为上一制导周期|σm|的取值；得到倾侧角翻转时机的校正量ΔE后，进行以下处理

Erev＝Erev,pre+Sign·ΔE

其中，Erev为倾侧角翻转时的能量，Erev,pre为上一制导周期得到的Erev；当飞行器的能量降到Eh时，通过调整攻角消除高度偏差

αf＝αf,pre+kh(hf-hF)

其中，αf为再入终端的攻角，αf,pre为上一制导周期的αf值，kh为反馈系数(比如-2×10^-6)，hF为要求的终端高度，为预测的终端高度。

所述步骤1)中，初始下降段倾侧角的|σini|计算方法为：

|σini|＝|σini|0+aΔCl+aΔCd+bΔρ+cΔθ0+dΔV0

其中，ΔV0为初始速度偏差，Δθ0为初始速度倾角偏差，ΔCl、ΔCd分别为升力系数、阻力系数偏差，Δρ为大气密度偏差，常数a、b、c、d反映各误差项对初始下降段的影响，通过仿真分析进行设置。

飞行器到目标点的视线角计算倾侧角的符号sign(σini)的计算方法为

sign(σini)＝-sign(ψ-ψLOS)

其中，ψLOS为飞行器到目标点的视线角。

轨迹预测时用到的控制量模型为

1)攻角模型为

其中，Ma为飞行马赫数，Maf为再入终端的马赫数，αf接近最大升阻比攻角，α0是一个可调节变量，为了减小热流，飞行器以大攻角再入大气层；

2)倾侧角模型为

其中，|σc|是当前时刻倾侧角的幅值，|σf|为终端的倾侧角幅值，根据终点的状态来初步确定，Em、|σm|为设计节点；

3)飞行器过程中，倾侧角翻转两次，第二次翻转应距离再入终点足够近(比如归一化能量为0.98)，翻转时机通过校正算法实时调节，在第一次翻转前，仅采用权利要求1中步骤9)的方法对第一次翻转时机进行校正，第二次翻转时机保持不变，第一次翻转后，开始采用权利要求1中步骤9)的方法对第二次翻转时机进行校正。

倾侧角的约束边界为

其中，K位地球自转的影响项，M为飞行器的质量，Sr为飞行器的参考面积，kQ为热流模型参数，qmax、nmax分别为最大热流、动压、过载约束。

航程偏差和横向位置计算公式为

其中，λ0、φ0为再入初始点的经度、纬度，λf、φf为预测的再入终点的经度、纬度。横向位置偏差在P坐标系(见参考文献[1])中求解，为φF在P坐标系中的表示，为φf在P坐标系中的表示，RE为地球半径。

与现有技术相比，本发明所具有的有益效果为：本发明设计了一种基于模糊控制器的预测-校正制导算法，其优点在于：(1)改进了传统预测-校正方法的思路，每一次校正只需一次轨迹预测，大幅度地减小了计算量。(2)该方法采用模糊控制器对飞行器运动进行三维校正，提高了制导算法的鲁棒性和灵活性。

附图说明

图1升力式再入过程图；

图2为本发明方法流程图；

图3(a)飞行器航程偏差的隶属度函数图；图3(b)飞行器剩余能量的隶属度函数图；图3(c)飞行器倾侧角调整量的隶属度函数图；图3(d)飞行器攻角调整量的隶属度函数图；图3(e)飞行器横向偏差的隶属度函数图；图3(f)飞行器翻转时机调整量的隶属度函数图；

图4(a)飞行器再入高度变化图；图4(b)飞行器再入地面轨迹图；图4(c)飞行器再入攻角变化图；图4(d)飞行器再入倾侧角变化图；图4(e)飞行器再入热流变化图；图4(f)飞行器再入过载变化图；

图5飞行器再入落点分布图。

具体实施方式

假定某可重复使用飞行器从空间返回再入，飞行状态包含高度h、经度λ、纬度φ、速度V、速度倾角θ和航向角ψ，其再入过程的运动方程可表示为：

其中，L和D分别为飞船再入过程中的升力和阻力，计算公式为

方程(1)中，Cθ、Cψ为地球旋转引起的哥氏加速度项，为地球旋转引起的牵连加速度项

如图2所示，针对本实施例中的再入飞行器，本发明的具体实施步骤如下：

S1.初始下降段制导。根据初始状态偏差和气动系数偏差计算初始下降段的倾侧角大小

|σini|＝|σini|0+aΔCL+aΔCD+bΔρ+cΔθ0+dΔV0 (3)

其中，|σini|0＝3°，各项偏差量均被归一化，a、b、c、d分别取为12、10、12、10。同时根据飞行器到目标点的视线角计算倾侧角的符号sign(σini)，在σini的制导作用下，飞行器不断下降，直到满足初始下降段的结束条件

S2.建立攻角和倾侧角的模型。

(S2-a)攻角模型为

其中，α0的初值为45°，αf的初值为15°。

(S2-b)倾侧角模型为

其中，E为归一化后的能量，Em＝0.8，|σm|的初值为π/4。

(S2-c)倾侧角翻转模型。飞行器过程中，倾侧角翻转两次，第一次翻转时机的初值为Erev＝0.6，第二次翻转时机的初值为Erev＝0.96。

S3.轨迹预测。进入滑翔段后，根据当前状态和加速度计的测量结果，更新大气密度和气动系数误差模型，确保这些模型与实际相符。然后，以当前点为起始点进行轨迹预测，基于S2中的控制量模型，采用龙哥库塔数值积分法，以能量为自变量对动力学方程进行积分，直到能量减少到TAEM要求的能量，然后停止积分，得到终端状态，计算航程偏差ΔR，高度偏差Δh、以及横向位置偏差CR。

S4.根据预测的终端状态对飞行参数进行校正。

(S4-a)预测的终端航向角更新再入终端位置，即进入TAEM区域的入口，确保飞行器垂直进入TAEM区域。

其中，RTAEM为TAEM的半径，取为100km。

(S4-b)根据预测结果校正制导指令，校正算法采用两个模糊控制器实现，模糊控制器A的输入为能量Eto-go、航程偏差ΔR，输出为倾侧角校正量Δσ和攻角校正量Δα。模糊控制器B的输入为横向位置偏差CR，输出为倾侧角翻转能量的变化量ΔE。所有变量的隶属度函数见附录图3，模糊控制器的规则如表1。

表1(a)倾侧角调整量的模糊规则表

表1(b)攻角调整量的模糊规则表

表1(c)倾侧角翻转时机调整量的模糊规则表

(S4-b-1)得到倾侧角校正量Δσ后，为了使指令连续，对其进一步处理

其中，Δtgud根据轨迹预测时长确定，取为1.5s，Δtsim取为0.5s。

(S4-b-2)在校正当前倾侧角时，同时对倾侧角剖面模型的节点进行调整，增大飞行器的调节能力。

|σm|＝|σm|pre+kmΔσ (9)

其中，km取为0.5，|σm|的最大值为85°。

(S4-b-3)计算倾侧角的约束边界，如果倾侧角的幅值超出边界，则取边界值

其中，kmax为线性分段函数，通过仿真分析确定。

(S4-b-4)得到攻角校正量Δα后，为了使指令连续，对其进一步处理

其中，α0∈[42°,50°]。

(S4-b-5)倾侧角翻转时机的确定。得到倾侧角翻转时机的校正量ΔE后，进行以下处理

第一次校正前，用上式校正第一次翻转时机，第二次翻转时机保持不变。第一次校正后，采用上式校正第二次翻转时机。

(S4-b-6)当飞行器的能量降到Eh时，通过调整攻角消除高度偏差

S5.将校正后的制导指令输送给高精度动力学方程，进行积分，一个制导周期完成。判断飞行器的能量是否达到TAEM接口的要求，若是，结束整个仿真过程，否则，转入S2，进入下一个制导周期。

为进一步说明本发明对可重复使用飞行器再入制导的作用，此处给出一个仿真算例。飞行器的质量为M＝37362.9kg，特征面积为Sr＝149.388m²，初始状态如下

h0＝121.51km，λ0＝-117.01°，φ0＝-18.225°，

V0＝7621.8m/s，θ0＝-1.4379°，ψ0＝-38.329°；

再入终端要求

Vf＝926m/s，hf＝30.48km；

着陆场位置

λT＝-80.138°，φT＝-28.61°；

热流、动压、过载约束为

qmax＝14364Pa，nmax＝2.5g0

仿真过程中，考虑的各种误差的类型、分布及大小如表1所示。

表2误差参数类型及分布

随机抽200组误差进行MonteCarlo数值打靶仿真。打靶仿真的统计结果如表3所示，从表中数据可知，高度和速度的制导精度较高。附图4和附图5给出了打靶仿真的结果。

表3 Monte-Carlo数值仿真打靶统计结果

参考文献：

[1]Y.Xie,L.H.Liu,J.Liu,G.J.Tang,et al.Rapid generation of entry trajectories with waypoint and no-fly zone constraints[J].Acta Astronautica,2012,77:167-181.