本发明涉及一种工业过程监测方法,尤其是涉及一种基于变量加权PCA模型的分散式工业过程监测方法。
背景技术:
在整个综合自动化系统中,故障检测系统可谓是必不可少的组成部分,因为实时监测生产过程的运行状态是保证生产安全和维持产品质量稳定的必要手段。随着科学技术的飞速发展,现代工业过程通常是由多个交错的生产单元组成,能精确描述其运行机理的物理模型是无法获取的。但是,得益于各种先进仪表与计算技术的广泛应用,工业过程可以测量和存储海量的数据样本。因此,在整个综合自动化系统中实施故障检测不再依赖于基于机理模型的过程监测方法。取而代之的是,以生产过程采样数据为核心的数据驱动的过程监测方法。作为数据驱动的过程监测方法的一个重要研究分支,多变量统计过程监测方法于近年来受到了工业界和学术界的广泛关注,其核心思想在于利用过程正常数据建立能描述过程正常运行状态的统计模型,从而实现对过程是否发生故障进行监测的目的。然而,现代工业过程因其流程的复杂性导致采样数据呈现出错综复杂的关系,这对传统多变量统计过程监测方法的实用性提出了挑战与质疑。如何更有效的挖掘数据潜藏的有用信息,并建立更实用的故障检测模型一直都在摸索中。
在现有的多变量统计过程监测方法体系中,主元分析(Principal Component Analysis,PCA)是最常用的数据分析算法,已被广泛用于工业过程监测实践中。近十几年来,基于PCA的故障检测方法以及其他延伸拓展形式层出不穷。例如,核PCA方法用于非线性过程监测、动态PCA方法用于应对采样间隔短的动态过程对象、分散式PCA方法应用于大规模工业过程监测、等等。值得指出的一点是,这些方法在开始实施之前,需将工业数据按变量进行标准化处理,即所有的测量变量都被归一化。从某种角度上看,所有测量变量其实都是被赋予了相同的权值,使统计分析方法在处理数据时同等对待各个测量变量。这种数据预处理方式对PCA这类旨在挖掘数据变量相关性的分析算法而言,有一个缺陷:数据变量间的相关性是存在差异的,若不对数据变量间的相关性差异进行有效的权衡,PCA算法所提取的潜藏信息无法全面而有效地描述过程运行的状态。基于分散式PCA的故障检测方法涉及对测量变量进行分块处理,将相关的测量变量聚类,能在一定程度上区分了变量间的相关性,它因此能取得优越于传统PCA方法的故障检测效果。但是,分散式PCA方法在建模过程中有两个问题还未得到深入研究探讨。首先,每个变量子块的相关性同样是有大小差异的,建立子块PCA模型时未加考虑;其次,变量分块要么依赖专家经验,要么需要一个截断阀值以区分变量间的相关与否。因此,基于PCA尤其是基于分散式PCA的过程监测方法所能取得故障检测效果还有待进一步的商榷。可想而知的是,若是能在实施PCA算法前,充分权衡变量间相关性的差异,在此基础上建立的PCA故障检测模型会具备更加可靠而优越的性能。
技术实现要素:
本发明所要解决的主要技术问题是:充分权衡变量相关性的差异并建立分散式的过程监测模型。为此,本发明提供了一种基于变量加权PCA模型的分散式工业过程监测方法,该方法首先以过程训练数据来计算测量变量间的相关性。然后,利用这些相关性数值对测量变量进行多样化的加权,并建立相应的PCA故障检测模型。最后,利用这多个PCA模型对生产过程是否发生故障进行分散式监测。
本发明解决上述技术问题所采用的技术方案为:一种基于变量加权PCA模型的分散式工业过程监测方法,包括以下步骤:
(1)在生产过程正常运行状态下,利用采样系统采集样本组成训练数据集X∈Rn×m,对矩阵X中每个变量进行标准化处理,得到均值为0,标准差为1的新矩阵其中,n为训练样本数,m为过程测量变量数,R为实数集,Rn×m表示n×m维的实数矩阵,为第k个变量的n个测量值组成的列向量,下标号k=1,2,…,m。
(2)初始化k=1后,按照下式计算第k个测量变量与中所有变量的相关性Ck,j:
其中,上标号T表示矩阵或向量的转置,下标号j=1,2,…,m,符号||||表示计算向量的长度,并将得到的m个相关性数值组成加权向量Ck=[Ck,1,Ck,2,…,Ck,m]。
(3)按照下式对矩阵中各变量进行加权处理得到新矩阵
其中,加权矩阵Wk=diag(Ck)为对角矩阵,对角线上的元素对应为向量Ck中各数值。
(4)为矩阵建立相应的PCA故障检测模型,保留模型参数以备在线监测时调用,其中dk为第k个PCA模型保留的主元个数,为相应的投影变换矩阵,为第i个PCA模型中dk个主元的协方差矩阵,与分别为第k个PCA模型中两个监测统计量的控制限。
(5)令k=k+1,若满足条件k≤m,则返回至步骤(2);反之,则保存得到的m个加权矩阵W1,W2,…,Wm以及m组不同的PCA故障检测模型参数Θ1,Θ2,…,Θm。
(6)收集新采样时刻的数据样本y∈R1×m,并对其进行同样的标准化处理得到
(7)利用m个不同的加权矩阵W1,W2,…,Wm分别对向量进行加权处理,对应可得到m个加权后的向量
(8)调用m组不同的PCA故障检测模型参数Θ1,Θ2,…,Θm,按照如下所示公式分别计算不同PCA模型对应的监测统计量:
至此,可得到m组不同的监测统计量。
(9)决策当前采样时刻数据是否正常,若所有统计量数值都满足条件和则当前数据是正常样本;反之,决策系统发生故障。
与传统方法相比,本发明方法的主要优势在于充分考虑了测量变量间的相关性差异,建立的PCA故障检测模型因而能较全面地提取过程数据中潜藏的有用信息。由于过程数据测量变量间的相关性是存在差异的,而PCA算法旨在挖掘过程数据间的相关性,若是未能充分考虑这种相关性差异强弱,PCA所提取的潜藏信息就无法全面而有效地描述过程运行状态。相比之下,本发明方法利用过程每个测量变量与其他测量变量间的相关性大小来对训练数据进行多样化的加权,可以突出的体现出测量变量间的相关性强弱。此外,利用多个PCA故障检测模型实施分散式过程监测可以较好的保证提取过程数据潜藏信息的多样性,从而实现对过程运行状态的全面性描述。可以说,本发明方法具备更全面的过程运行状态描述能力,会取得更加可靠而优越的故障检测效果。
附图说明
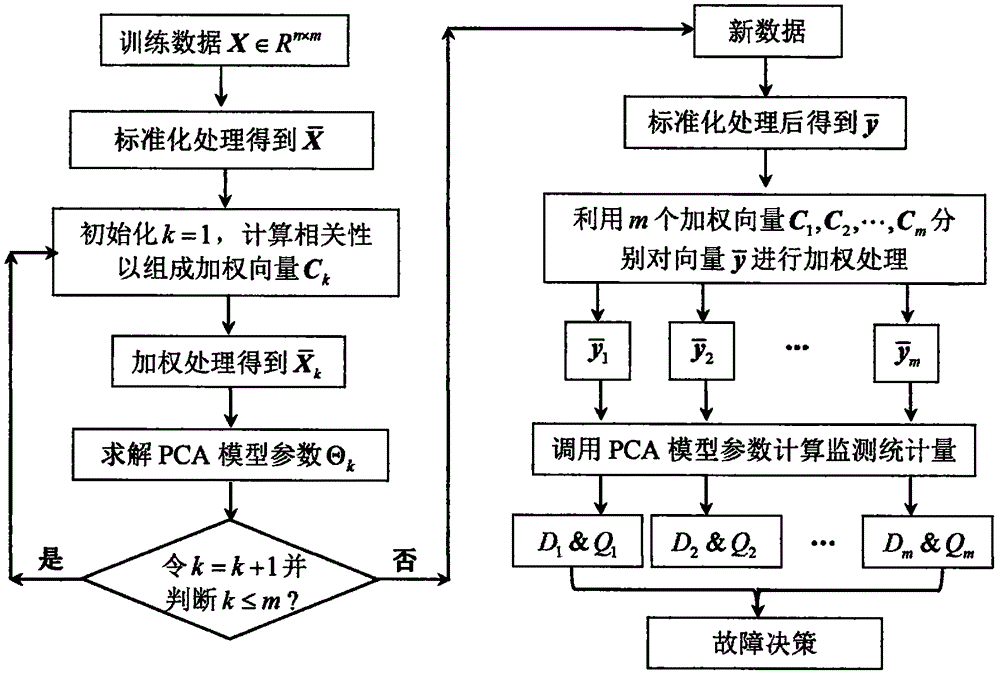
图1为本发明方法的实施流程图。
具体实施方式
下面结合附图对本发明方法进行详细的说明。
如图1所示,本发明涉及了一种基于变量加权PCA模型的分散式工业过程监测方法,该方法的具体实施步骤如下所示:
步骤1:在生产过程正常运行状态下,利用采样系统采集样本组成训练数据集X∈Rn×m,对矩阵X中每个变量进行标准化处理,得到均值为0,标准差为1的新矩阵其中,n为训练样本数,m为过程测量变量数,R为实数集,Rn×m表示n×m维的实数矩阵,为第k个变量的n个测量值组成的列向量,下标号k=1,2,…,m。
步骤2:初始化k=1后,按照下式计算第k个测量变量与中所有变量的相关性Ck,j:
其中,上标号T表示矩阵或向量的转置,下标号j=1,2,…,m,符号||||表示计算向量的长度,并将得到的m个相关性数值组成加权向量Ck=[Ck,1,Ck,2,…,Ck,m]。
步骤3:按照下式对矩阵中各变量进行加权处理得到新矩阵
上式中,加权矩阵Wk=diag(Ck)为对角矩阵,对角线上的元素对应为向量Ck中各数值。
步骤4:为矩阵建立相应的PCA故障检测模型,保留模型参数以备在线监测时调用,其中dk为第k个PCA模型保留的主元个数,为相应的投影变换矩阵,为第k个PCA模型中dk个主元的协方差矩阵,与分别为第k个PCA模型中两个监测统计量的控制限。求解PCA模型的具体实施方式如下所示:
首先,计算的协方差矩阵
其次,求解Sk所有非零特征值λ1>λ2>…>λN所对应的特征向量p1,p2…,pN,其中,N为非零特征值的个数;
再次,设置保留的主成分个数dk为满足条件的最小值,并将对应的dk个特征向量组成投影变换矩阵
然后,计算主成分的协方差矩阵Λi=TkTTk/(n-1),并按照下式计算控制限与
其中,表示置信度为α、自由度分别为dk与n-dk的F分布所对应的值,表示自由度为h、置信度为α为卡方分布所对应的值,M和V分别为Qi统计量的估计均值和估计方差;
最后,保留模型参数以备调用。
步骤5:令k=k+1,若满足条件k≤m,则返回至步骤(2);反之,则保存得到的m个加权矩阵W1,W2,…,Wm以及m组不同的PCA故障检测模型参数Θ1,Θ2,…,Θm。
步骤6:收集新采样时刻的数据样本y∈R1×m,并对其进行同样的标准化处理得到
步骤7:利用m个不同的加权矩阵W1,W2,…,Wm分别对向量进行加权处理,即:
其中,k=1,2,…,m,对应可得到m个加权后的向量
步骤8:调用m组不同的PCA故障检测模型参数Θ1,Θ2,…,Θm,按照如下所示公式分别计算不同PCA模型对应的监测统计量:
至此,可得到m组不同的监测统计量。
步骤9:决策当前采样时刻数据是否正常,若所有统计量数值都满足条件和则当前数据是正常样本;反之,决策系统发生故障。
上述实施例只用来解释本发明,而不是对本发明进行限制,在本发明的精神和权利要求的保护范围内,对本发明做出的任何修改和改变,都落入本发明的保护范围内。