攻角的线性自抗扰控制方法与流程

本发明涉及航空航天领域，特别涉及攻角的线性自抗扰控制方法。
背景技术：
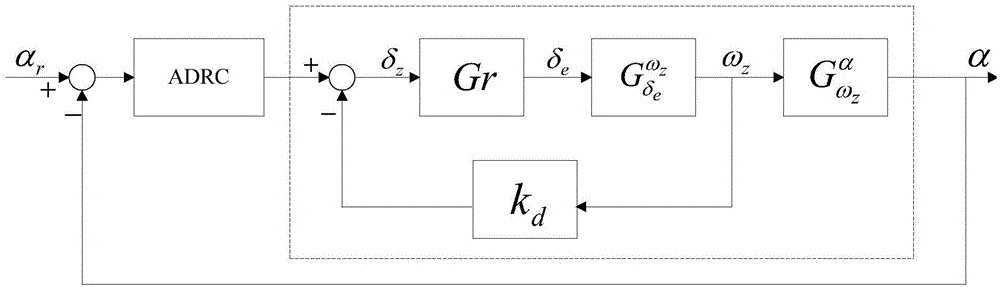
：飞行器的攻角控制在工程上具有很成熟的控制设计技术，但是设计方法普遍对于设计人员的经验和技术能力要求比较苛刻，设计周期、难度和成本都比较高。规范、简洁、高性能和强鲁棒的攻角控制设计方法具有十分重要的迫切需求。自抗扰控制(ActiveDisturbanceRejectionControl,ADRC)起因于现代控制中基于模型的复杂控制算法在工程上难以得到应用，而工程上普遍使用的最简单的PID控制由于结构所限，难以实现高性能的控制品质。中国科学院系统科学研究所的韩京清研究员最初改造PID控制的主要思路是，通过引进非线性反馈，特别是分数幂非光滑反馈，形成“小误差，大增益；大误差，小增益”的设计思想，提高反馈效率，并取得了显著的效果。为了消除积分反馈的不利影响，韩京清研究员巧妙地借鉴了反馈线性化的思想，通过实时估计系统的动态特性，引进了扩张状态观测器(ExtendedStateObserver,ESO)的思想，这形成了ADRC的关键和精华所在，但依然使用非线性观测器。无需量测外扰而能消除其影响；根据对象的输入输出信号用扩张状态观测器实时估计扰动作用并给予补偿，从而去抑制扰动所引起的输出误差：“自抗扰控制器”由此得名。这里扰动是指包括内扰和外扰的总和作用。ADRC的优点是不必精确了解被控对象的动态特性(内扰)，也无需量测外扰的作用，可以同时抑制所有扰动。ADRC易实现非线性、时变、大时滞等控制难度大的对象的控制，不必另加任何功能环节，简单地就可以实现。该控制器实际上把那些非线性、时变、时滞所带来的影响都当作干扰来处理。针对原始ADRC使用非线性反馈所带来的稳态高增益容易在小信号引起抖动同时控制参数过多的问题(一般形式的非线性ADRC的控制参数达到12个，不太利于工程应用)，以及非线性控制器难以进行工程上常用的频域分析以确定稳定性边界的不足，美国ClevelandStateUniversity的高志强教授将所有控制器和ESO都以线性形式实现，大幅度地将控制参数降到4个，而且都有比较明确的物理意义，十分便于工程应用。工程上使用较多的也是线性ADRC(LinearADRC,LADRC)，其中ESO在其中发挥了巨大作用。线性控制使得频域分析便于操作，也就容易确定工程上十分关心的稳定边界。LADRC尽管是线性形式，但是由于采用了ESO，可以把一定时间尺度以内的不确定性和非线性估计出来并直接进行补偿，这与标准非线性控制方法(非自适应情形)需要对于非线性建模并明晰其动力学系数特性的方法相比明显简化，不再专门区分线性与非线性。技术实现要素：根据本发明实施例提供的攻角的线性自抗扰控制方法及装置，目的在于实现一种供工程应用的简便的攻角控制设计方法，同时具有强鲁棒性和优异的动态品质。根据本发明实施例提供的攻角的线性自抗扰控制方法，包括：在飞行器飞行期间，获取飞行器当前俯仰角速度和当前攻角；对所述当前攻角和预配置的期望攻角的差值进行自抗扰控制处理，得到自抗扰控制值；将所述自抗扰控制值和所述当前俯仰角速度的反馈值的差值输入相应传递函数进行处理，得到下一时刻俯仰角速度；根据所述下一时刻俯仰角速度，确定所述飞行器的下一时刻攻角。优选地，所述的对所述当前攻角和预配置的期望攻角的差值进行自抗扰控制处理，得到自抗扰控制值包括：将所述当前攻角与期望攻角相减，得到攻角差值；将所述攻角差值输入至自抗扰控制函数，进行自抗扰控制处理，得到自抗扰控制值。优选地，所述自抗扰控制函数如下：δz0=δz1-z2K]]>其中，所述是自抗扰控制值；Kp是比例控制增益，α是攻角，αr是期望攻角；z2是对扩张状态-rα的估计；r代表近似之后被控对象的开环频带；K是对α放大系数的近似估计。优选地，所述的将自抗扰控制值和所述当前俯仰角速度的反馈值的差值输入相应传递函数进行处理，得到下一时刻俯仰角速度包括：将所述当前俯仰角速度与微分反馈系数相乘，得到所述当前俯仰角速度的反馈值；将所述自抗扰控制值和所述当前俯仰角速度的反馈值相减，得到下一时刻升降舵控电压；将所述下一时刻升降舵控电压输入至舵机的传递函数进行处理，得到下一时刻升降舵偏；将所述下一时刻升降舵偏输入至由升降舵偏至俯仰角速度的传递函数进行处理，得到下一时刻俯仰角速度。优选地，所述舵机的传递函数的Gr(s)如下：Gr(s)=δeδz]]>其中，s代表拉普拉斯变换算子；δe是升降舵偏；δz是升降舵控电压。优选地，所述由升降舵偏至俯仰角速度的传递函数如下：Gδeωz(s)=Gδzωz(s)=ωzδz=p(s+b)s2+a1s+a0]]>其中，s代表拉普拉斯变换算子，是俯仰力矩对于δz的偏导数；是升力系数对于δz的偏导数；aα是俯仰力矩对于α的偏导数；bα是升力系数对于α的偏导数；是俯仰力矩对于ωz的偏导数。优选地，所述的根据所述下一时刻俯仰角速度，确定所述飞行器的下一时刻攻角包括：将所述下一时刻俯仰角速度输入至由俯仰角速度到攻角的传递函数进行处理，得到下一时刻攻角。优选地，所述由俯仰角速度到攻角的传递函数如下：Gωzα(s)=αωz=bδzs+aωzbδz+aδzp(s+b)]]>其中，s代表拉普拉斯变换算子；α是攻角；ωz是俯仰角速度；是俯仰力矩对于ωz的偏导数；是俯仰力矩对于δz的偏导数；是升力系数对于δz的偏导数；aα是俯仰力矩对于α的偏导数；bα是升力系数对于α的偏导数；是俯仰力矩对于ωz的偏导数。根据本发明实施例提供的存储介质，其存储用于实现上述攻角的线性自抗扰控制方法的程序。本发明实施例提供的技术方案具有如下有益效果：本发明实施例提供一种攻角的线性自抗扰控制律，能够保证攻角准确跟踪期望值，与现有技术相比，提高了攻角跟踪精度，且控制设计流程标准化。附图说明图1是本发明实施例提供的攻角的线性自抗扰控制方法框图；图2是本发明实施例提供的攻角线性自抗扰控制框图；图3是本发明实施例提供的攻角的定点阶跃响应图；图4是本发明实施例提供的非线性仿真中攻角响应曲线图；图5是本发明实施例提供的非线性仿真中俯仰舵曲线图。具体实施方式以下结合附图对本发明的优选实施例进行详细说明，应当理解，以下所说明的优选实施例仅用于说明和解释本发明，并不用于限定本发明。针对常规布局飞机、无人机或者导弹等飞行器，本发明实施例的攻角的线性自抗扰控制包括以下步骤：步骤1:针对非线性方程描述的飞行器动力学，得到纵向短周期运动的独立小扰动线性动力学方程。针对一般飞行器的非线性方程描述，根据小扰动线性化原理，得到纵向短周期运动的独立小扰动线性动力学方程，如公式1所示。其中，α是攻角；是俯仰角；是俯仰角加速度；是俯仰角速度；θ是弹道倾角；是弹道倾角角速度；δe是升降舵偏，由升降舵控电压δz驱动；ωz是俯仰角速度，aα,分别是俯仰力矩对于α、δe和ωz的偏导数，bα,分别是升力系数对于α和δe的偏导数。通过公式1可以得到开环传递函数，如公式2和公式3所示，本实施例的舵机传递函数时间常数远小于飞行器本体，因此近似认为δe≈δz。Gδeωz(s)≈Gδzωz(s)=ωzδz=p(s+b)s2+a1s+a0---(2)]]>Gωzα(s)=αωz=bδzs+aωzbδz+aδzp(s+b)---(3)]]>其中，舵机传递函数Gr(s)满足δe＝Gr(s)δz；s代表拉普拉斯变换算子，步骤2:选取合适的角速度反馈系数，得到此情况下的闭环系统特性，称为广义对象，即由于陀螺测量噪声比较强，因此根据陀螺测量噪声强度引入合适微分反馈系数，一般选取不超过1.0的微分反馈系数kd，产生角速度反馈项kdωz形成人工阻尼，得到阻尼改善的闭环广义对象，如公式4所示。ωzδz0=p(s+b)s2+(a1+kdp)s+(a0+kdpb)≈p(s+b)s+r---(4)]]>其中，代表角速度反馈项kdωz补偿之后的等效控制量，r代表近似之后被控对象的开环频带，综合公式3和公式4(即将二者相乘)，并考虑到的量级很小，得到公式5。αδz0≈aωzbδz+aδzs+r---(5)]]>步骤3：对于步骤2得到的广义对象，设计扩张状态观测器，对扩张状态进行估计，将扩张状态估计值适当缩放后用于广义对象反馈补偿，使得补偿后的广义对象(即)成为单积分器。公式5的时域形式中除了控制量的直接作用项外，其他一律归入扩张状态，具体地说，选取与控制量无关的项-rα为扩张状态，并采用如公式6的降阶扩张状态观测器对存在不确定性的扩张状态-rα进行估计。z·=-ωoz-ωo2α-ωoKδz0z2=z+ωoα---(6)]]>其中，是对于α放大系数的近似估计，ωo是观测器带宽，z代表中间变量，没有实际的物理意义，代表z的导数，z2就是对于扩张状态-rα的估计。为将被控对象(即公式5)转换成标准的积分环节，选取虚拟控制其中，代表针对积分环节的虚拟控制变量，则得到公式7。αδz1≈1s---(7)]]>步骤4：最后对于补偿后的广义对象使用比例控制(对于单积分器，一个比例控制即可消除静差，实现良好的动态品质)，与前面的观测器补偿及角速度反馈共同构成攻角的线性自抗扰控制。选取其中，αr是期望攻角，Kp代表比例控制增益，综合和得到整个控制律的线性形式，如公式8所示。δz=Kp(αr-α)-z2K-kdωz---(8)]]>图1是本发明实施例提供的攻角的线性自抗扰控制方法框图，如图1所示，步骤包括：步骤S101：在飞行器飞行期间，获取飞行器当前俯仰角速度ωz和当前攻角α。步骤S102：对所述当前攻角α和预配置的期望攻角αr的差值进行自抗扰控制处理，得到自抗扰控制值步骤S102包括：将所述当前攻角α与期望攻角αr相减，得到攻角差值(αr-α)，并将所述攻角差值(αr-α)输入至自抗扰控制函数进行自抗扰控制处理，得到自抗扰控制值。其中，是自抗扰控制值；Kp是比例控制增益，α是攻角，αr是期望攻角；z2是对扩张状态-rα的估计；r代表近似之后被控对象的开环频带；K是对α放大系数的近似估计。步骤S103：将所述自抗扰控制值和所述当前俯仰角速度的反馈值的差值输入相应传递函数进行处理，得到下一时刻俯仰角速度。步骤S103包括：将所述当前俯仰角速度ωz与微分反馈系数kd相乘，得到所述当前俯仰角速度的反馈值kdωz，将所述自抗扰控制值和所述当前俯仰角速度的反馈值kdωz相减，得到下一时刻升降舵控电压δz，将所述下一时刻升降舵控电压δz输入至舵机的传递函数进行处理，得到下一时刻升降舵偏δe，将所述下一时刻升降舵偏δe输入至由升降舵偏至俯仰角速度的传递函数进行处理，得到下一时刻俯仰角速度ωz。其中，s代表拉普拉斯变换算子；是俯仰力矩对于δz的偏导数；是升力系数对于δz的偏导数；aα是俯仰力矩对于α的偏导数；bα是升力系数对于α的偏导数；是俯仰力矩对于ωz的偏导数。步骤S104：根据所述下一时刻俯仰角速度，确定所述飞行器的下一时刻攻角。步骤S104包括：将所述下一时刻俯仰角速度ωz输入至由俯仰角速度到攻角的传递函数进行处理，得到下一时刻攻角α。本领域普通技术人员可以理解，实现上述实施例方法中的全部或部分步骤是可以通过程序来指令相关的硬件来完成，所述的程序可以存储于计算机可读取存储介质中，该程序在执行时，包括步骤S101至步骤S104。其中，所述的存储介质可以为ROM/RAM、磁碟、光盘等。图2是本发明实施例提供的攻角的线性自抗扰控制装置框图，图2从宏观上说明了整个控制的信号流，包括：ADRC模块、Gr模块、模块、模块、kd模块。ADRC模块，用于将当前攻角α和预配置的期望攻角αr的差值输入进行自抗扰控制处理，得到自抗扰控制值kd模块，用于将所述当前俯仰角速度ωz与微分反馈系数kd(即角速度反馈系数)相乘，得到所述当前俯仰角速度的反馈值kdωz。Gr模块，用于将所述自抗扰控制值和所述当前俯仰角速度的反馈值kdωz的差值输入至舵机的传递函数进行处理，得到下一时刻升降舵偏δe。模块，用于将所述下一时刻升降舵偏δe输入至由升降舵偏至俯仰角速度的传递函数进行处理，得到下一时刻俯仰角速度ωz。模块，用于将所述下一时刻俯仰角速度ωz输入至由俯仰角速度到攻角的传递函数进行处理，得到下一时刻攻角α。所述装置的工作过程如下：步骤201：采集当前俯仰角速度ωz和当前攻角α。步骤202：将期望攻角αr与当前攻角α相减，得到攻角差值(αr-α)作为ADRC模块的输入，进行自抗扰控制处理，得到自抗扰控制值并将当前俯仰角速度ωz输入至kd模块，将当前俯仰角速度ωz与微分反馈系数kd相乘，得到当前俯仰角速度的反馈值kdωz。步骤203：将自抗扰控制值与当前俯仰角速度的反馈值kdωz相减，并将差值作为Gr模块的输入，由Gr模块处理后得到下一时刻升降舵偏δe。步骤204：将下一时刻升降舵偏δe输入至模块，由模块处理后得到下一时刻俯仰角速度ωz。步骤205：将下一时刻俯仰角速度ωz输入至模块，由模块处理后得到下一时刻攻角α，实现对攻角α的控制。本发明实施例涉及航空航天领域的飞行器攻角控制技术，适用于快速的设计过程实现，系统对于气动参数不确定性鲁棒性强。图3是本发明实施例提供的攻角的定点阶跃响应图，如图3所示，说明了对于线性小扰动模型的定点阶跃响应特性，通过使用本实施例提出的方法，可以通过固定的控制参数使得不同工作点的攻角响应在1s内收敛到期望值，响应速度快，而且不同特征点的响应差别小。图4是本发明实施例提供的非线性仿真中攻角响应曲线图，如图4所示，说明了对于非线性的响应特性，通过使用本实施例提出的方法，可以保证攻角响应的平稳。图5是本发明实施例提供的非线性仿真中俯仰舵曲线图，如图5所示，对应于图4的控制量曲线，通过使用本文提出的技术，可以保证俯仰舵平稳而且需要的控制能量小。尽管上文对本发明进行了详细说明，但是本发明不限于此，本
技术领域：
技术人员可以根据本发明的原理进行各种修改。因此，凡按照本发明原理所作的修改，都应当理解为落入本发明的保护范围。当前第1页1 2 3