一种磁力线圈结合动量轮的航天器姿态联合控制方法与流程

本发明涉及航天器姿态控制技术领域，特别涉及一种磁力线圈结合动量轮的航天器姿态联合控制方法。

背景技术：

磁控方式主要用于大卫星章、进动消除及动量轮卸载，直接采用纯磁控进行三轴稳定控制的航天器相对较少。近几年，微小型航天器发展迅速，由于微小型航天器体积小、质量轻、功耗低等约束，微小型航天器尤其是微纳航天器在进行姿态控制时，多采用纯磁控作为其姿态控制方式。为了进一步提高微小型航天器姿态稳定度，动量轮结合磁控的控制方式逐渐得到了更广泛的应用。同纯磁控相比，该方法具有姿态稳定度高、控制方式简单等优点，但当前磁力线圈同动量轮进行姿态控制时，不同通道的姿态控制独立进行，导致动量轮控制通道姿态收敛速度快、指向精度高，而磁控制通道收敛速度慢、指向精度低、抗干扰能力弱。同时当前的磁控与其它控制相结合控制方式多不适宜完成大角度快速机动任务，限制航天器在轨任务拓展及后续发展。

微小型航天器空间任务多样化，灵活化和精细化趋势对微小型航天器的空间操作能力提出了新的要求，当前采用磁控结合其它简单控制方式来实现航天器快速姿态稳定及姿态指向成为了一种迫切的需求。

技术实现要素：

本发明针对上述现有技术中存在的问题，提出一种磁力线圈结合动量轮的航天器姿态联合控制方法，控制方式简单，对航天器的导航系统、控制系统等无额外需求，可综合利用星上资源，节约工质，具有算法先进、控制精度高、姿态收敛速度快的优点。

为解决上述技术问题，本发明是通过如下技术方案实现的：

本发明提供一种磁力线圈结合动量轮的航天器姿态联合控制方法，其包括以下步骤：

S11：获取航天器的姿态信息，同时获取所述航天器所处轨道环境的磁场信息；

S12：将所述姿态信息带入控制律中解算出期望的姿态控制力矩；

S13：根据所述期望的姿态控制力矩反算出磁力线圈的期望输出；

S14：根据所述磁力线圈的期望输出以及所述磁力线圈的输出限制得出所述磁力线圈的实际输出；

S15：根据所述期望的姿态控制力矩以及所述磁力线圈的实际输出反算出动量轮的期望输出；

S16：根据所述动量轮的期望输出以及所述动量轮的输出限制得出所述动量轮的实际输出；

S17：根据所述磁力线圈的实际输出以及所述动量轮的实际输出对所述航天器的姿态进行联合控制。

较佳地，所述步骤S17之后还包括：

S18：重复步骤S11-S17，直至所述航天器的姿态收敛期望范围。

较佳地，所述步骤S11中获取的所述航天器的姿态信息包括：姿态四元素q和姿态角速度ω，所述磁场信息包括：磁场强度Bb。

较佳地，所述步骤S12中的控制律为PD控制律，所述期望的姿态控制力矩为：

Texp＝-Kpq-Kdω，

其中，Kp和Kd分别为姿态四元素q和姿态角速度ω对应的系数矩阵。

较佳地，所述步骤S13中：所述磁力线圈为三轴磁力线圈，所述磁力线圈的期望输出Mex为使目标函数达到最小时得出的，所述目标函数为：

其中，Mexx、Mexy、Mexz分别为Mex的xb轴分量、yb轴分量、zb轴分量。

较佳地，所述步骤S14中的所述磁力线圈的输出限制为输出最大值Mmax的限制，所述磁力线圈的实际输出为：

式中，Mex为所述磁力线圈的期望输出，函数max(|Mex|)表示向量Mex中元素绝对值最大者。

较佳地，所述步骤S15中：所述动量轮为单轴动量轮；

当所述单轴动量轮置于xb轴时，所述动量轮的期望输出为：

当所述单轴动量轮置于yb轴时，所述动量轮的期望输出为：

当所述单轴动量轮置于zb轴时，所述动量轮的期望输出为：

其中，Mmx、Mmy、Mmz分别为所述磁力线圈的实际输出Mm的xb轴分量、yb轴分量、zb轴分量，Texpx、Texpy、Texpz分别为所述期望的姿态控制力矩Texp的xb轴分量、yb轴分量、zb轴分量。

较佳地，所述步骤S16中的所述动量轮的输出限制为输出最大值的限制，所述动量轮的实际输出为：

其中，为所述动量轮的期望输出。

相较于现有技术，本发明具有以下优点：

(1)本发明提供的磁力线圈结合动量轮的航天器姿态联合控制方法，为以磁力线圈和动量轮为执行机构的航天器姿态协同控制方法，解决以磁力线圈和动量轮为姿态控制执行机构时对航天器快速姿态稳定或姿态指向问题，无需额外设备和功耗，对航天器姿态测量系统及控制系统无额外要求，具有算法先进、控制精度高等优点；

(2)本发明采用动量轮通磁力线圈系统控制的方式，能够实现航天器三自由度的快速控制，弥补采用纯磁控仅能提供垂直磁场面内控制力矩的不足，能够在姿态执行机构简单的情形下，实现三自由度较高精度的姿态控制，在微钠型航天器姿态控制领域中有着巨大的应用前景。

当然，实施本发明的任一产品并不一定需要同时达到以上所述的所有优点。

附图说明

下面结合附图对本发明的实施方式作进一步说明：

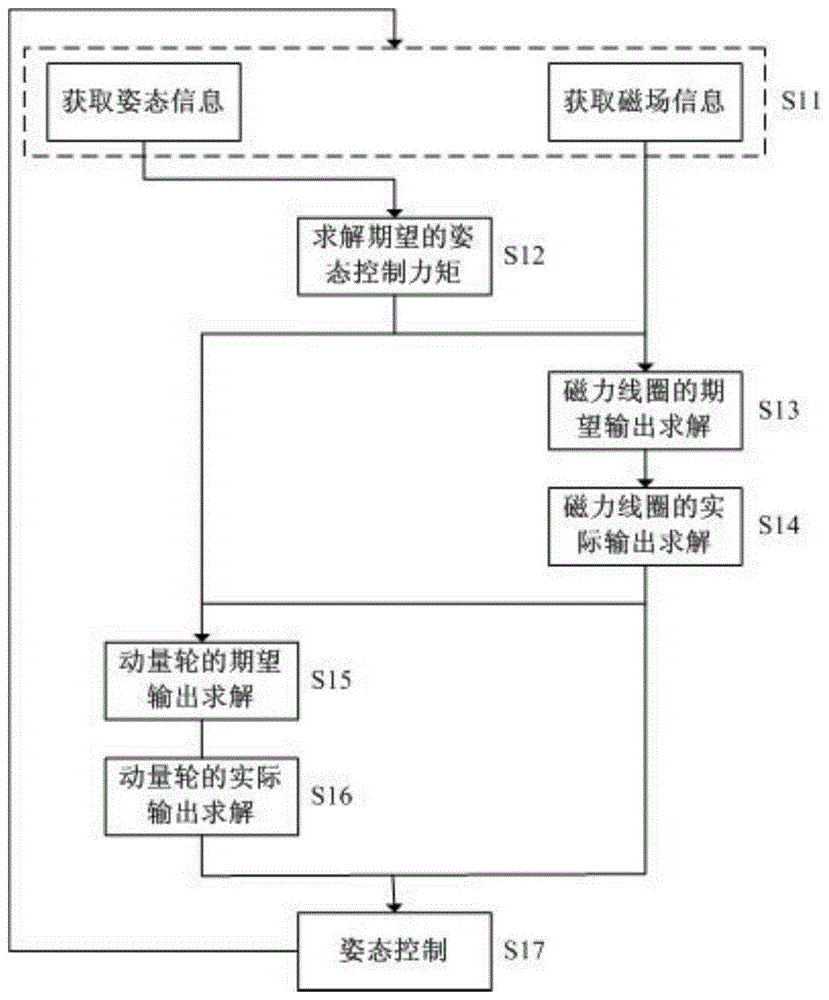
图1为本发明的实施例的磁力线圈结合动量轮的航天器姿态联合控制方法的流程图；

图2为本发明的实施例的体坐标系示意图；

图3为本发明的实施例的航天器的姿态角速度仿真曲线图；

图4为本发明的实施例的航天器的姿态四元素仿真曲线图；

图5为本发明的实施例的磁力线圈的实际输出仿真曲线图；

图6为本发明的实施例的置于yb轴的动量轮的实际输出仿真曲线图；

图7为本发明的实施例的置于yb轴的动量轮的角动量变化仿真曲线图。

具体实施方式

下面对本发明的实施例作详细说明，本实施例在以本发明技术方案为前提下进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。

结合图1-图7，对本发明的磁力线圈结合动量轮的航天器姿态联合控制方法进行详细描述，如图1所示为其流程图，其包括以下步骤：

S11：依据控制律需求，获取航天器体坐标系相对惯性系的姿态四元数q和角速度ω信息，同时获取航天器体坐标系下的磁场强度矢量Bb。该过程在ts时间段内完成。ts依据实际情况选定。

S12：将姿态信息q和ω带入控制律得期望的姿态控制力矩Texp；本实施例中，控制律选用飞行器相对惯性空间定向的PD控制律，即期望的姿态控制力矩Texp＝-Kpq-Kdω，其中Kp和Kd分别为两种姿态信息对应的系数矩阵，期望的姿态控制力矩Texp在体坐标系下三轴对应分量分别为：Texpx、Texpy、Texpz。

S13：磁力线圈的期望输出为使目标函数达到最小时，以偏置动量轮置于yb轴为例，将磁场强度Bb和期望控制力矩Texp带入(1)式解得三轴磁力线圈期望输出Mex；

其中，E＝Bby/Bbx，F＝-Texpz/Bbx，H＝-TexpzBbz/(BbxBby)-Texpx/BbyG＝Bbz/Bby，此时可利用期望姿态控制力矩确切得到Texpx、Texpz。

S14：结合三轴磁力线圈的输出最大值Mmax的限制，得出磁力线圈实际输出Mm。由式(2)确定磁力线圈实际输出Mm，

式中，函数max(|Mex|)表示向量Mex中元素绝对值最大者。

S15：将磁力线圈实际输出Mm、磁场强度Bb、期望控制力矩Texp带入式(3)得动量轮期望输出

此时，yb轴的期望姿态控制力矩Texpy通过动量轮同磁力矩线圈的协同作用而确切得到。

S17：由于动量轮受输出最大值的限制，将期望的姿态控制力矩及动量轮输出最大值带入式(4)得动量轮输出

S17：将磁力线圈以Mm矢量输出、动量轮以输出，进行姿态控制，时间长度为tc。tc依据实际情况选定。

执行完步骤S17后，重新返回步骤S11进行姿态测量工作，如此不断循环，直至航天器的姿态收敛至期望范围。

如图2所示为体坐标系的示意图，磁力线圈以及动量轮协同输出获得期望的姿态控制力矩的示意在图中示出。

上述实施例中，是以动量轮置于yb轴为例，由于坐标系定义的任意性，可类似得出将动量轮置于xb轴以及zb轴的情况，此处不再赘述。

进一步的，给出更为具体的算例，对本发明进行详细描述。取期望的姿态控制力矩的控制律的控制参数Kp＝diag([3×10^-5 5×10^-4 3×10^-5])，Kd＝diag([8×10^-4 5×10^-4 8×10^-4])；动量轮标称转速为0；动量轮最大输出磁力线圈最大输出Mmax＝0.2A·m²；ts＝0.2s；tc＝0.8s；期望的姿态指向四元数[1 0 0 0]^T；起始姿态四元数姿态角速度ω0＝[0.01 0.01 0.01]^Trad/s。航天器的惯量矩阵取：

设COTV同末子级分离时，COTV体坐标系相对惯性系姿态四元数。地磁场模型取2015年10阶TGRF国际地磁场参考模型。

通过循环执行步骤S11至S17，分别得到姿态机动过程星体角速度、姿态四元数、磁力矩线圈输出、动量轮输出及角动量变化仿真结果分别如图3、图4、图5、图6、图7所示。由仿真结果可得：经过300s左右的姿态控制，体坐标系x轴和z轴姿态指向精度小于0.05°，角速度小于0.01°/s。一般的动量轮结合磁力矩线圈控制方式需要经过2～3个轨道周期即11000s至17000s左右姿态才能收敛且达到相应精度，证明了本发明的有效性及优势所在。

此处公开的仅为本发明的优选实施例，本说明书选取并具体描述这些实施例，是为了更好地解释本发明的原理和实际应用，并不是对本发明的限定。任何本领域技术人员在说明书范围内所做的修改和变化，均应落在本发明所保护的范围内。