一种基于导前扰动模型的火电机组汽温预测函数控制算法的制作方法

本发明涉及火电机组的控制领域，具体地说是一种基于导前扰动模型的火电机组汽温预测函数控制算法。

背景技术：

大型火电机组汽温对象具有大迟延、大惯性和时变性，对于主汽温控制系统来说，具有导前区和惰性区，当导前区汽温存在较大的纯迟延，或者特性变化较大时，常规串级PID控制或预测函数控制调节机构出现震荡，严重时会使整个系统不稳定。

技术实现要素：

针对上述现有技术存在的情况，本发明提供一种基于导前扰动模型的火电机组汽温预测函数控制算法，当对象特性变化较大时，本发明的算法较常规串级PID算法具有较大的优越性。

为此，本发明采用如下的技术方案：一种基于导前扰动模型的火电机组汽温预测函数控制算法，包括如下步骤：

1)建立导前区汽温预测模型、惰性区汽温预测模型及包含导前区和惰性区汽温对象特性的广义预测模型，所述的导前区汽温预测模型是用来近似导前区汽温对象特性的数学模型；所述的惰性区温度模型是用来近似惰性区汽温对象特性的数学模型；所述的广义预测模型为整个汽温系统汽温对象特性的近似数学模型，即将导前区汽温预测模型和惰性区汽温预测模型合并为一个模型；

2)将实际导前区汽温和导前区汽温预测模型输出汽温的偏差ED作为惰性区汽温预测模型的扰动信号源，根据惰性区汽温预测模型和广义预测模型获得最优控制律；

3)在最优控制律的基础上进行简化，将指数系数简化为乘数系数，将预测时域优化长度简化为预测调整系数，得到简化的最优控制律。

本发明的算法简单，参数调整方便，能够更好的适应工况需求，提高控制品质。本发明通过调整预测调整系数实现对汽温对象的优化控制。

将本发明的算法应用于主汽温控制系统，通过与常规串级PID算法得到的控制性能对比，证明了本发明算法具有优良的性能。

进一步地，所述的导前区汽温预测模型如下：

式中，K_m1为模型增益，T_m1为模型惯性时间，T_dm1为模型纯迟延时间(s为积分因子)；

所述的惰性区汽温预测模型如下：

式中，K_m2为模型增益，T_m2为模型惯性时间，T_dm2为模型纯迟延时间；

所述的广义预测模型如下：

式中，K为模型增益，T为模型惯性时间，T_d为模型纯迟延时间。

进一步地，当采用一个基函数时，有：

u(k+i)＝u(k)，i＝1,2,…,H-1，

ED(k+i)＝ED(k)，i＝1,2,…,H-1，

上式中，k表示采样时刻，H表示预测时域步长。

广义预测模型、惰性区汽温预测模型的预测输出分别为：

上式中，α为广义模型G(s)差分方程系数，α_m2为惰性区模型G_m2(s)差分方程系数。

预测模型的总输出为：

y_m(k+H)＝y₀(k+H)+y_m2(k+H)，

根据优化指标的极值获得最优控制律为：

上式中，c为设定值，β为系统期望闭环动态特性，y(k)为被控量，y₀(k)为广义预测模型输出，y_m2(k)为惰性区预测模型输出，y_m(k)为y₀(k)和y_m2(k)叠加后输出，ED(k)为实际导前区汽温和导前区汽温预测模型输出汽温的偏差。

进一步地，所述的预测调整系数包括参考轨迹预测调整系数b和控制预测调整系数a，简化的最优控制律如下：

上式中，T_s为采样周期，T_R为参考轨迹时间常数；

本发明具有以下有益效果：不需要串级控制中的内回路，当导前区汽温存在较大的纯迟延时控制系统仍稳定；保证了汽温预测函数控制系统具有较强的鲁棒性；提高了主汽温系统的控制品质。当对象特性变化较大时，本发明的算法较常规串级PID算法具有较大的优越性。

附图说明

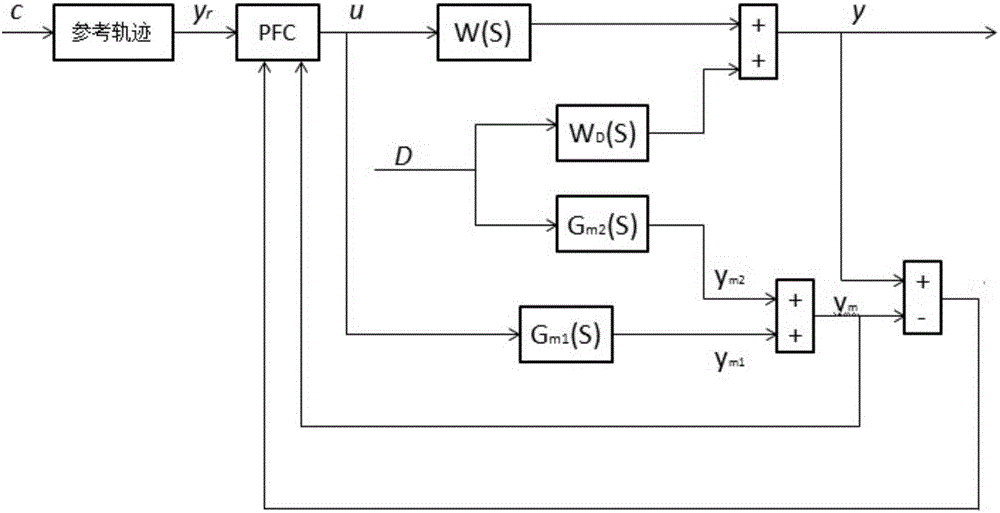
图1为常规带扰动预测函数控制系统原理图(图中，c为设定值，y_r为参考轨迹，u为最优控制量，D为扰动信号源，y_m2为扰动模型输出，y_m1为对象模型输出，y_m为模型总输出，y为被控对象输出，W(s)为被控对象传递函数，W_D(s)为系统扰动通道传递函数。)

图2为本发明基于导前扰动模型的汽温预测函数控制系统原理图(图中，c为设定值，y_r为参考轨迹，u为最优控制量，ED为扰动信号源，y_m2为惰性区汽温预测模型输出，y₀为广义预测模型输出，y_m为模型总输出，y为被控对象输出，W₁(s)为导前区传递函数，W₂(s)为惰性区传递函数。)

图3为模型不变时串级PID与本发明对比控制效果图(图中，A为本发明响应曲线，B为串级PID响应曲线)。

图4为模型变化时串级PID与本发明对比控制效果图(图中，A为本发明响应曲线，B为串级PID响应曲线)。

具体实施方式

下面结合说明书附图和具体实施方式对本发明作进一步说明。

一、常规带扰动预测函数控制算法

根据图1，当控制系统的外部扰动信号可测时，可以通过试验确定系统的扰动模型，此时系统具有两个模型，即对象模型G_m1(s)和扰动模型G_m2(s)，假定均为一阶加迟延模型，即：

当采用一个基函数时，有：

u(k+i)＝u(k) i＝1,2,…,H-1

D(k+i)＝D(k) i＝1,2,…,H-1 (3)

各模型的预测输出为：

预测模型输出为：

y_m(k+H)＝y_m1(k+H)+y_m2(k+H) (5)

根据优化指标的极值可以获得最优控制律为：

二、本发明基于导前扰动模型的汽温预测函数控制算法

根据图2，G_m1(s)是导前区汽温预测模型，用来近似导前区汽温对象特性的数学模型；G_m2(s)是惰性区温度模型，用来近似惰性区汽温对象特性的数学模型；G(s)是广义预测模型，为整个汽温系统汽温对象特性的近似数学模型，即将导前区汽温预测模型和惰性区汽温预测模型合并为一个模型。扰动信号源为实际导前汽温和导前区汽温预测模型输出汽温的偏差，该信号作用于本发明的预测控制系统，对比图2可以推导出该预测控制系统控制的控制律。

此时扰动信号可测，即为实际导前汽温和导前区汽温预测模型输出汽温的偏差ED，此时预测控制系统具有两个模型，即广义预测模型G(s)和惰性区温度模型G_m2(s)，假定均为一阶加迟延模型，即：

当采用一个基函数时，有：

u(k+i)＝u(k) i＝1,2,…,H-1

ED(k+i)＝ED(k) i＝1,2,…,H-1 (8)

各模型的预测输出为：

预测模型输出为：

y_m(k+H)＝y₀(k+H)+y_m2(k+H) (10)

根据优化指标的极值可以获得最优控制律为：

本发明在上述最优控制律的基础进行简化设计，将指数系数简化为乘数系数，将预测时域优化长度简化为预测调整系数，分别为参考轨迹预测调整系数b和控制预测调整系数a，经简化后设计出的最优控制律如下：

在上式中，T_s为采样周期，T_R为参考轨迹时间常数，一般设置为4～12秒；在调整控制系统品质时，只需调整预测调整系数a和b，便可获得良好的控制品质。

三、本发明控制算法与串级PID控制对比

将本发明控制算法应用于某主汽温对象，进行仿真研究。汽温对象的导前区传递函数为

惰性区传递函数为：

在常规串级汽温控制系统中，内回路采用PI控制器，比例系数为3，积分系数为0.01；外回路采用PI控制器，比例系数为0.5，积分系数为0.004。

采用图2所示的预测函数控制系统，首先对广义预测模型进行拟合简化，得到等效的一阶加纯迟延对象模型为：

导前区汽温预测模型为：

惰性区汽温预测模型为：

PFC的三个预测模型取为：K＝-0.13，T＝30，T_d＝120；K_m1＝-0.12，T_m1＝23，T_dm1＝180；K_m2＝0.6，T_m2＝45，T_dm2＝120；PFC采用一个基函数，采样周期设置为6，参考轨迹时间常数为12，参考轨迹预测调整系数b为3，控制预测调整系数a为2，进行控制系统阶跃响应实验，获得的控制对比曲线如图3所示。图3中，本发明算法响应速度明显快于串级PID响应，抑制扰动的能力也比串级PID算法强。

为了考验控制系统性能，需要在对象模型失配后，对两种控制系统进行阶跃响应实验。由于模型增益失配对控制系统影响最大，因此将模型增益失配后两种控制系统的阶跃响应曲线进行对比。保持预测函数控制系统和串级控制系统主、副回路控制器参数不变，将控制对象导前区传递函数模型增益增大30％至0.39，进行阶跃响应实验获得控制对比曲线如图4所示。图4中，模型变化后，本发明控制响应基本不受影响，串级PID控制响应已经有发散的趋势。