一种面向敏捷卫星多目标任务规划的差分进化方法与流程

本发明涉及一种面向敏捷卫星多目标任务规划的差分进化方法。

背景技术：

敏捷卫星多目标规划问题具有明显的时间依赖的特征，分析时间依赖调度方法的研究现状对敏捷卫星多目标规划研究的帮助较大。当前关于时间依赖调度方法的研究，主要为时间依赖加工时间、时间依赖的收益以及时间依赖的转换时间三个方面的研究。Gupta和Browne最早提出时间依赖的加工时间,后续的学者对问题的扩展形式进行了研究，研究的目标函数主要分为最小化完工时间之和与最小化加工周期，加工时间对加工开始时间的依赖关系以线性关系为主，也有Huang、Toskar等学者研究了指数型的依赖关系。对于这些问题，许多研究者提出了启发式算法，也有像Hindi采用了如模拟退火的智能算法来解决呈线性递减关系的加工时间依赖问题。

在时间依赖的收益研究上，主要考虑了时间依赖惩罚与时间依赖价值两种情况。Yang对单资源环境下以最小化加权延期惩罚与资源超期使用惩罚之和为目标的调度问题进行了研究，提出采用局部搜索算法来寻找加工序列。Tanaka提出了一种两阶段过程的最优化求解算法，该算法在寻找最优解时具有较好的表现，但是对于大规模问题计算较慢。Hendel设计了基于领域的局部搜索算法来解决具有不同交货期的工件加工问题。在比较新的研究中，Germs采用简单的启发式规则来解决具有严格交货期以及批加工转换时间的订单受理与调度问题，Wang采用一种分支定界最优算法来求解两台流水加工机器环境下的订单受理与调度问题，但是考虑的工件加工转换时间不具有。

对于时间依赖的转换时间研究相对较少，Black研究了一种名为TD-PARP(Time-Dependent Prize-Collecting Arc Routing Problem)的问题，采用一种基于变邻域搜索的优化方法和一种基于禁忌搜索的优化方法来求解该问题，考虑的转换时间由表给出。Pralet在面对时间依赖的转换时间问题时，采用一种时间依赖的简单时间网络来处理，对应在敏捷卫星中采用约束传播来调整后一成像任务的开始时间，然而并没有考虑对问题的优化模型及算法。陈成研究了具有时间依赖转换时间与时间依赖收益的工件加工问题，设计了混合差分算法，并将其应用到敏捷卫星成像任务规划上，具有很好地求解效果，缺陷在于考虑的目标仅仅为点目标成像的单目标规划，无法适用多目标的情况。

技术实现要素：

本发明的目的是提供一种面向敏捷卫星多目标任务规划的差分进化方法，将多目标优化特征集于一体分析，以输出指定数目的个体。

为实现上述目的，本发明提供了如下方案：

一种面向敏捷卫星多目标任务规划的差分进化方法，所述差分进化方法包括：

步骤一：将敏捷卫星多目标任务的决策变量构成的解集空间转换为以混合编码的个体为单元的种群；

步骤二：对所述种群及种群的算法参数分别进行初始化；其中，所述种群的算法参数包括差分变异算子选择概率M_de、缩放因子F_c、交叉重组概率C_r、一般变异概率M_nor、种群规模N_pop以及迭代总数N_iter；

步骤三：根据差分变异算子选择概率M_de和缩放因子F_c生成捐赠向量根据交叉重组概率C_r将捐赠向量与目标向量进行组合得到试用向量根据一般变异概率M_nor对试用向量进行一般变异操作得到子代O_g；

步骤四：将子代O_g添加到所述种群Pop中得到变异种群Pop′，对个体解码得到适应度；

步骤五：判断当前迭代次数i是否小于迭代总数N_iter，若满足执行步骤六，否则执行步骤七；

步骤六：采用锦标赛排序方法对变异种群Pop′中个体进行选择，生成新的种群Pop，并更新对应的种群的算法参数，重复执行步骤三；

步骤七：剔除精英解集Archive中被支配的解，将所述变异种群Pop′中的非支配解添加到未被精英解集Archive中个体支配的解中以更新精英解集Archive；

步骤八：根据拥挤距离对精英解集Archive中的个体进行排序，并根据顺序输出指定数目的个体。

可选的，所述捐赠向量试用向量及子代O_g的生成数量与所述种群的规模一致。

可选的，对所述种群进行初始化的方法为完全随机方法或限定随机方法；其中，

(1)完全随机方法，对于初始种群中第i个体P_0,i，其第j维变量的生成方式为

其中，randn[1,n_j]表示生成随机整数处于范围[1,n_j]内，rand[0,1]表示生成的随机数处于范围[0,1]内；

(2)限定随机方法，针对于区域目标而言，分两种情况：

第一限定随机方法：对于所有区域目标对应编码中的分量在所有分解角度为固定同向分解角度对应的观测方式中随机选择；

第二限定随机方法：在异向分解角度对应的观测方式中随机选择。

可选的，对完全随机方法、第一限定随机方法及第二限定随机方法在种群初始化中采用0.8:0.1:0.1的比例来进行初始种群的生成。

可选的，所述捐赠向量根据以下两种差分变异公式确定捐赠向量

其中，i表示种群个体序号；

在精英解集中随机选择，差分变异算子选择概率M_de的初始值为0.2，并且在每次迭代中进行更新。

可选的，每次迭代中进行更新的方法包括：

若采用两种方式变异得到捐赠向量后成功进入到下一代的数目分别为m₁和m₂，没有进入到下一代的数目分别为w₁和w₂，则采用以下方式确定差分变异算子选择概率M_de：

累计20代后根据公式(3)更新，之后每代的差分变异算子选择概率M_de的更新根据上一代统计信息更新，不进行累计。

可选的，所述得到试用向量的方法包括：

假设参与重组的目标向量为

参与重组的捐赠向量为

根据以下公式组合得到

其中，i表示种群个体序号，j表示维度序号；

采用高斯分布的交叉重组概率C_r：

C_r·i＝GausseRand(u_cr,σ_cr)------------(5)；

公式(5)中将记录每一代中没有被一般变异生成子代替代并成功进入下一代的试用向量所使用的交叉概率C_r·i，形成集合累计20代后u_cr采用以下方式更新：

之后的每次更新仅仅根据上一代的统计进行。

可选的，对于试用向量采用以下一般变异得到变异个体来增加其种群多样性

其中，i表示种群个体序号，j表示维度序号；

比较一般变异后的个体与试用向量之间的支配关系，若无法支配则成为新子代个体；

一般变异概率M_nor采用以下方式生成：

M_nor·i＝GausseRand(u_nor,σ_nor)------------(8)；其中，u_nor与σ_nor为变异系数；公式(5)中将记录每一代成功替代试用向量时对应的一般变异概率M_nor·i，形成集合累计20代后u_nor采用以下方式更新

之后的每次更新仅仅根据上一代的统计进行。

可选的，所述采用锦标赛排序方法对变异种群Pop′中个体进行选择的方法包括：

采用锦标赛排序算法进行选择，选择时采用经典NSGA-Ⅱ算法使用的基于Pareto秩与拥挤距离的非支配排序算法，从变异种群Pop′中随机选择的多个个体中选择Pareto秩最小拥挤距离最大的个体进入到下一代种群中。

根据本发明提供的具体实施例，本发明公开了以下技术效果：

本发明面向敏捷卫星多目标任务规划的差分进化方法将敏捷卫星多目标任务的决策变量构成的解集空间转换为以混合编码的个体为单元的种群，在适应度评估也就是解码的过程中处理复杂的时间依赖型时间约束问题，进化过程中通过差分变异、交叉重组与一般变异相结合的方式增加种群多样性，通过排序选择保持物种的进化方向，同时采用精英解集记录求解过程中的非支配个体，整个过程中算法参数以自适应方式调整。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。

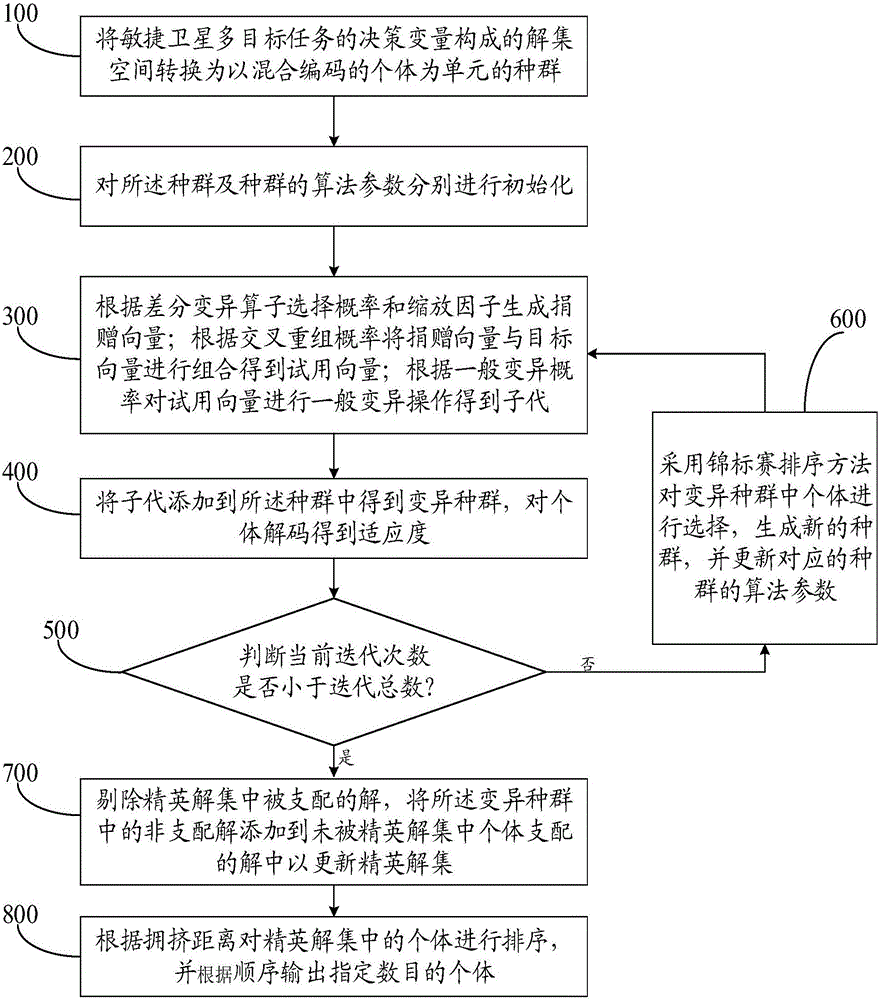
图1为本发明面向敏捷卫星多目标任务规划的差分进化方法的流程图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明的目的是提供一种面向敏捷卫星多目标任务规划的差分进化方法，将敏捷卫星多目标任务的决策变量构成的解集空间转换为以混合编码的个体为单元的种群，在适应度评估也就是解码的过程中处理复杂的时间依赖型时间约束问题，进化过程中通过差分变异、交叉重组与一般变异相结合的方式增加种群多样性，通过排序选择保持物种的进化方向，同时采用精英解集记录求解过程中的非支配个体，整个过程中算法参数以自适应方式调整。

为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。

如图1所示，本发明面向敏捷卫星多目标任务规划的差分进化方法包括：

步骤100：将敏捷卫星多目标任务的决策变量构成的解集空间转换为以混合编码的个体为单元的种群。

步骤200：对所述种群及种群的算法参数分别进行初始化；其中，所述种群的算法参数包括差分变异算子选择概率M_de、缩放因子F_c、交叉重组概率C_r、一般变异概率M_nor、种群规模N_pop以及迭代总数N_iter。

步骤300：根据差分变异算子选择概率M_de和缩放因子F_c生成捐赠向量根据交叉重组概率C_r将捐赠向量与目标向量进行组合得到试用向量根据一般变异概率M_nor对试用向量进行一般变异操作得到子代O_g；所述捐赠向量试用向量及子代O_g的生成数量与所述种群的规模一致。

步骤400：将子代O_g添加到所述种群Pop中得到变异种群Pop′，对个体解码得到适应度。

步骤500：判断当前迭代次数i是否小于迭代总数N_iter，若满足执行步骤600，否则执行步骤700。

步骤600：采用锦标赛排序方法对变异种群Pop′中个体进行选择，生成新的种群Pop，并更新对应的种群的算法参数，重复执行步骤300。

步骤700：剔除精英解集Archive中被支配的解，将所述变异种群Pop′中的非支配解添加到未被精英解集Archive中个体支配的解中以更新精英解集Archive。

步骤800：根据拥挤距离对精英解集Archive中的个体进行排序，并根据顺序输出指定数目的个体。

在处理中，对每个需求处理得到可行的分解结果，不可行的需求予以剔除，存在可行分解的需求数目为J。对于种群中的每个个体可以表示为：

当中表示第j个可行需求选择的观测方式，以整数编码且为实数，在观测方式下，需求开始观测时间窗口为其与需求开始观测时间的关系为

这样可以确保需求开始观测时间一直处于开始观测窗口内，需求的观测持续时间可以通过观测可行性验证获得。

在步骤200中，对所述种群进行初始化的方法为完全随机方法或限定随机方法；其中，

(1)完全随机方法，对于初始种群中第i个体P_0,i，其第j维变量的生成方式为：

其中，randn[1,n_j]表示生成随机整数处于范围[1,n_j]内，rand[0,1]表示生成的随机数处于范围[0,1]内；

(2)限定随机方法，针对于区域目标而言，分两种情况：

第一限定随机方法：对于所有区域目标对应编码中的分量在所有分解角度为固定同向分解角度对应的观测方式中随机选择；

第二限定随机方法：在异向分解角度对应的观测方式中随机选择。

在本实施例中，对完全随机方法、第一限定随机方法及第二限定随机方法在种群初始化中采用0.8:0.1:0.1的比例来进行初始种群的生成。

进一步地，在步骤300中，所述捐赠向量根据以下两种差分变异公式确定捐赠向量

其中，i表示种群个体序号；

在精英解集中随机选择，差分变异算子选择概率M_de的初始值为0.2，并且在每次迭代中进行更新。

其中更新的具体方法包括：

若采用两种方式变异得到捐赠向量后成功进入到下一代的数目分别为m₁和m₂，没有进入到下一代的数目分别为w₁和w₂，则采用以下方式确定差分变异算子选择概率M_de：

累计20代后根据公式(3)更新，之后每代的差分变异算子选择概率M_de的更新根据上一代统计信息更新，不进行累计。

其中，采用高斯分布的缩放因子，即F_c＝GausseRand(u_F,σ_F)，其中，u_F与σ_F为缩放系数。为了能够精细搜索，u_F的选取不宜过大，在本实施例中u_F＝0.8，σ_F＝0.3的参数配置，但并不以此为限。

进一步地，所述得到试用向量的方法包括：

假设参与重组的目标向量为

参与重组的捐赠向量为

根据以下公式组合得到

其中，i表示种群个体序号，j表示维度序号。

采用高斯分布的交叉重组概率C_r：

C_r·i＝GausseRand(u_cr,σ_cr)------------(5)；

公式(5)中将记录每一代中没有被一般变异生成子代替代并成功进入下一代的试用向量所使用的交叉概率C_r·i，形成集合累计20代后u_cr采用以下方式更新：

之后的每次更新仅仅根据上一代的统计进行。

进一步地，对于试用向量采用以下一般变异得到变异个体来增加其种群多样性。

比较一般变异后的个体与试用向量之间的支配关系，若无法支配则成为新子代个体。

一般变异概率M_nor采用以下方式生成：

M_nor·i＝GausseRand(u_nor,σ_nor)------------(8)；其中，u_nor与σ_nor为变异系数；公式(8)中将记录每一代成功替代试用向量时对应的一般变异概率M_nor·i，形成集合累计20代后u_nor采用以下方式更新：

之后的每次更新仅仅根据上一代的统计进行。

可选的，所述采用锦标赛排序方法对变异种群Pop′中个体进行选择的方法包括：采用锦标赛排序算法进行选择，选择时采用经典NSGA-Ⅱ算法使用的基于Pareto秩与拥挤距离的非支配排序算法，从变异种群Pop′中随机选择的多个个体中选择Pareto秩最小拥挤距离最大的个体进入到下一代种群中。

为了保持解不退化，采用精英解集保留每代中的优质个体，在每代选择操作之前，采用非支配排序后的Pareto非支配解来更新精英解集，更新规则为以下两条：剔除精英解集中被种群中Pareto非支配解支配的精英个体；添加种群中未被精英解集中个体支配的Pareto解到精英集中。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。

本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，根据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。