基于高斯分布的设备运行控制系统和方法与流程

本发明涉及设备的运行控制领域，尤其涉及一种基于高斯分布的设备运行控制系统和方法。

背景技术：

近年来，随着设备自动化水平的不断提高，对设备的控制精度要求也在不断提高。尤其在自动化水平相对较低的污水处理行业，如何提高设备的控制精度更是运营管理人员所关注的，特别是对于耗能较高的提升泵、鼓风机等设备。

设备的运行控制，需要根据工况进行调整，以污水处理厂的鼓风机为例，当进水中COD浓度较低时，需要适当调节降低鼓风机频率或风量。当时如何根据COD浓度变化以及其他水质指标变化情况，来调整鼓风机频率，彼此的相关关系如何一直是阻碍鼓风机等设备提高控制精度的难点。水质指标与鼓风机运行频率或风量的量化对应关系，多利用经验进行比对，进行定量化设定，灵活性较差，且与实际出入较大。从不同水质出现频率来看，呈现出一定的概率分布，且较为接近正态分布，由于不同区域和污水来源的而不同，因此针对不同的水质提供一种通用的方法。

技术实现要素：

本发明提供了一种基于高斯分布的设备运行控制方法和系统，以实现对设备运行的持续性高精度控制，实现设备运行与设备运行环境参数的匹配度提高。

本发明实施例提供了一种基于高斯分布的设备运行控制系统和方法，包括：

通过数据采集装置获取和设备运行相关的工况环境参数的数据信息；

建立混合高斯分布模型；

基于非线性最小二乘法计算混合高斯分布模型系数，得到混合高斯分布函数；

根据混合高斯分布函数控制设备运行；

混合高斯分布函数更新。

本发明通过数据采集和处理、建立混合高斯分布模型、基于非线性最小二乘法计算高斯分布模型系数、根据混合高斯模型控制设备运行等步骤，通过将多个高斯分布进行线性组合，得到“混合高斯分布模型”，并通过非线性最小二乘法对模型系数进行计算，降低计算复杂度；根据工况环境参数进行模型建立、系数计算，避免人为主观性；根据混合高斯分布函数控制设备运行，实现对设备运行更精准的控制，实用性强，控制精度高等优点；高斯分布函数更新，实现对混合高斯分布函数的持续更新，实现控制精度的持续保持，保障混合高斯分布函数与当前设备运行工况参数的高度符合。

附图说明

图1是本发明实施例一提供的基于高斯分布的设备运行控制系统和方法的流程图；

图2是本发明实施例二提供的基于高斯分布的设备运行控制系统和方法的流程图；

具体实施方式

下面结合附图和实施例对本发明作进一步的详细说明。可以理解的是，此处所描述的具体实施例是示例性的，仅仅用于解释本发明，而非对本发明的限定。

实施例一

图1为本发明实施例一提供的基于高斯分布的设备运行控制系统和方法的流程图，本实施例可适用于环保设施、厂区中设备的运行控制，该方法可以由服务器来执行，具体包括如下步骤：

步骤S101、通过数据采集装置获取和设备运行相关的工况环境参数的数据信息。

通过与仪器仪表远程交互，以实时获取和设备运行相关的工况环境参数的数据信息；

其中，所述工况环境参数的数据信息由于种类较多且需要实时多次测量获取，优选的通过数据采集装置在第一时间获取并传输到服务器中；

优选的是，所述采集，即可以是通过硬件实施采集电表、检测仪表数据，也可以是通过网络通信等方式获取数据库等在线数据，以及气体数据获取方式；

根据所述服务器中数据信息，进行初步的滤波处理，去除异常数据。

步骤S102、建立混合高斯模型。

1)建立高斯分布模型；

混合高斯分布模型是多个高斯分布的线性组合，对于高斯分布的概率密度函数表达式，如式(1)所示

其中，x为样本点，μ_i为样本均值，σ_i²为样本方差；

2)建立混合高斯分布模型

混合高斯分布概率密度函数表示为

其中，X为总体样本，a_i为第i指标的高斯分布的影响因子，μ_i为第i个指标的高斯分布的均值，为第i个指标高斯分布的方差，k为高斯分布个数，当k＝1时，混合高斯分布模型f(X)＝N(μ,σ)即为一维高斯分布的概率密度函数。

步骤S103、基于非线性最小二乘法计算混合高斯分布模型系数，得到混合高斯分布函数。

1)根据所述工况环境参数的数据信息，记为X，作为输入训练数据；

2)根据非线性最小二乘法，计算每个工况环境参数的高斯分布模型系数，得到高斯分布的概率密度函数式；

3)根据工况环境不同参数对设备运行控制的影响，为不同参数分配不同的影响因子系数；

4)根据工况环境不同参数的高斯分布的概率密度函数式和不同工况环境参数的影响因子系数，计算混合高斯分布模型系数，得到混合高斯分布函数。

步骤S104、根据混合高斯分布函数控制设备运行。

1)选取设备运行关键可调节参数指标，记为设备参数Y；

2)构建设备参数Y与工况环境参数混合高斯分布概率间的关系，表达式为

其中，X′为设备运行的当前工况环境参数的数据信息，Y_max为设备运行中设备参数可调节的范围上限值，Y_min为设备参数可调节范围下限值，f(X)为工况参数混合高斯分布函数；

3)根据所述公式(3)和设备运行的当前工况环境参数的数据信息，计算得到设备参数Y(X′)；

4)调节设备根据所述计算得到的设备参数Y(X′)运行。

步骤S105、根据当前工况环境参数与历史工况环境参数作为模型输入训练数据，根据非线性最小二乘法，计算每个工况环境参数的高斯分布模型系数，得到高斯分布的概率密度函数式，更新混合高斯分布函数系数，提高控制精准度。

步骤S106、根据设备使用状态，设定高斯分布函数系数更新的时间周期T₁，优选的所述时间周期T₁的范围为0.5h-24h，设定设备参数调节的时间周期T₂，优选的所述时间周期T₂的范围为0.5h-72h。

本实施例的技术方案，解决了对设备运行控制的精准化控制，根据实时工况环境调节设备运行状态，实现设备相对工况环境最优化运行，解决设备运行的精准控制问题。

实施例二

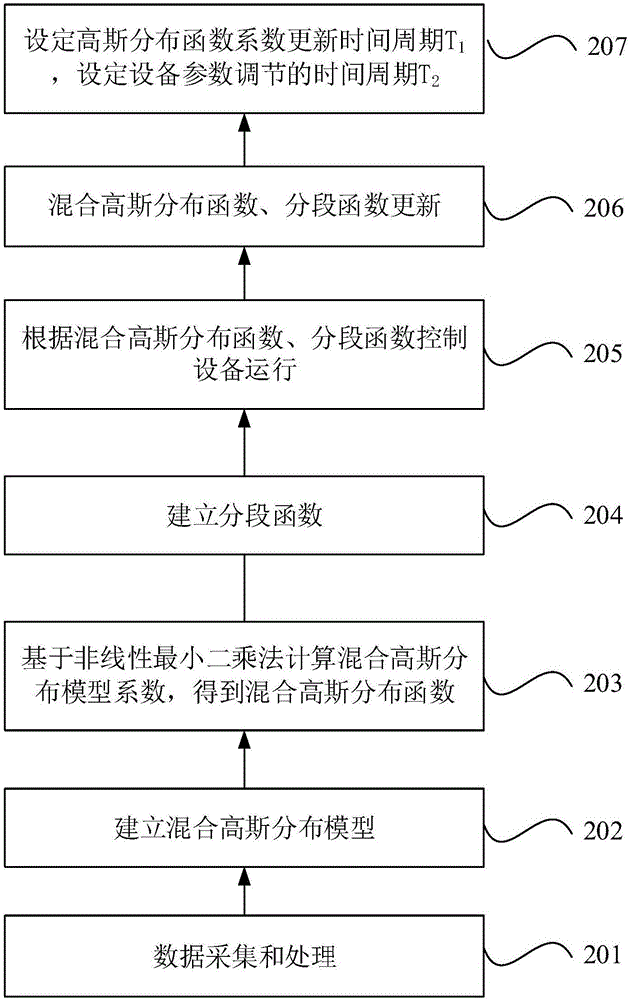
图2为本发明实施例二提供的基于高斯分布的设备运行控制系统和方法的流程图，本实施例可适用于环保设施、厂区中设备的运行控制，该方法可以由服务器来执行，具体包括如下步骤：

步骤S201、通过数据采集装置获取和设备运行相关的工况环境参数的数据信息。

通过与仪器仪表远程交互，以实时获取和设备运行相关的工况环境参数的数据信息。

其中，所述工况环境参数的数据信息由于种类较多且需要实时多次测量获取，优选的通过数据采集装置在第一时间获取并传输到服务器中。

其中，优选的是，所述采集，即可以是通过硬件实施采集电表、检测仪表数据，也可以是通过网络通信等方式获取数据库等在线数据，以及气体数据获取方式。

根据所述服务器中数据信息，进行初步的滤波处理，去除异常数据。

步骤S202、建立混合高斯模型。

混合高斯分布模型是多个高斯分布的线性组合，对于高斯分布的概率密度函数表达式，如式(1)所示；

混合高斯分布概率密度函数表示为式(2)；

步骤S203、基于非线性最小二乘法计算混合高斯分布模型系数，得到混合高斯分布函数。

1)根据所述工况环境参数的数据信息，记为X，作为输入训练数据；

2)根据非线性最小二乘法，计算每个工况环境参数的高斯分布模型系数，得到高斯分布的概率密度函数式；

3)根据模型评价指标，计算模型精度，模型评价指标计算公式如下：

Q＝∑[y_i-N(x_i,μ,σ)]² (4)

其中，x_i是样本点，为模型输入，表示工况环境参数的数据信息，N(x_i,μ,σ)为模型输出，是根据高斯分布的概率密度函数式计算得到的概率值，y_i为工况参数x_i的实际概率值；

优选的是，当Q(x_i)≤θ，判断工况环境参数符合高斯分布模型；当Q(x_i)>θ，判断工况参数不符合高斯分布模型；其中，x_i为工况环境参数，θ为精度阈值；优选的θ的范围为0～μ。

4)根据所述符合高斯分布模型的工况环境不同参数对设备运行控制的影响，为不同参数分配不同的影响因子系数；

5)根据所述符合高斯分布模型的工况环境参数的影响因子和高斯分布模型系数，计算混合高斯分布函数f(X_n)，其中，X_n为符合高斯分布模型的工况环境参数样本；

步骤S204、构建分段函数

根据不符合高斯分布模型的工况环境参数的数据信息构建分段函数g(X_b)，表达式为

其中，X_b为不符合高斯分布模型的工况环境参数样本，x′_l为第l个不符合高斯分布模型的工况环境参数的当前数据信息值，x_lj为第l个不符合高斯分布模型的工况环境参数的分段边界值，g_j为分段函数的函数值。

步骤205、根据混合高斯分布函数和分段函数控制设备运行。

1)选取设备运行关键可调节参数指标，记为设备参数Y；

2)构建设备参数Y与工况环境参数混合高斯分布概率和分段函数间的关系，表达式为

其中，m为分段函数所分段数，X_n′为符合高斯分布的工况参数的当前数据信息值，X′_b为不符合高斯分布的工况参数的当前数据信息值，f_j为每段边界值，g_j为每段分段函数值，Y_max为设备运行中设备参数可调节的范围上限值，Y_min为设备参数可调节范围下限值，Y_j为每阶段设定运行参数值；

优选的是，Y_j的计算公式为；

Y_j＝λ_fY_f+λ_gY_g (6)

其中，λ_f、λ_g为不同类型工况环境参数权重，λ_f+λ_g＝1，Y_f为符合高斯分布模型的工况环境参数与设备参数的关系函数，Y_g为不符合高斯分布模型的工况环境参数与设备参数的关系函数，Y_g＝g(X_b)*(Ymax-Ymin)+Ymin

3)根据所述公式(5)和设备运行的当前工况环境参数的数据信息，计算得到设备参数Y(X′)；

4)调节设备根据所述计算得到的设备参数Y(X′)运行

步骤S206、根据当前工况环境参数与历史工况环境参数作为模型输入训练数据，根据非线性最小二乘法，计算每个工况环境参数的高斯分布模型系数，得到高斯分布的概率密度函数式，更新混合高斯分布函数系数，提高控制精准度；同时根据数据信息更新分段函数。

步骤S207、根据设备使用状态，设定高斯分布函数系数更新的时间周期T₁，优选的所述时间周期T₁的范围为0.5h-24h，设定设备参数调节的时间周期T₂，优选的所述时间周期T₂的范围为0.5h-72h。

本实施例的技术方案，解决了对设备运行控制的精准化控制，根据实时工况环境调节设备运行状态，实现设备相对工况环境最优化运行，解决设备运行的精准控制问题。

实施例三

本实施例可以以上述实施例为基础，提供一种优选实例，用以实现污水处理厂鼓风机的运行控制。

步骤S301、数据采集和处理

通过与仪器仪表远程交互，以实时获取和设备运行相关的工况环境参数的数据信息，并第一时间获取并传输到服务器中。

优选的是，数据信息采集间隔为1min。

对采集数据进行初步的滤波处理，去除异常数据。

优选的是，本实施例中选择的工况环境参数指标为污水处理厂进水COD量和进水氨氮量。

步骤S302、建立混合高斯模型。

1)建立高斯分布模型

混合高斯分布模型是多个高斯分布的线性组合，进水COD量的高斯分布的概率密度函数表达式，如式(7)所示

进水氨氮量的高斯分布的概率密度函数表达式为

其中，C_COD为进水COD量数据样本点、C_NH为进水氨氮量数据样本点，μ₁、μ₂为进水COD量数据均值、进水氨氮量数据均值，σ₁²、σ₂²为进水COD量、进水氨氮量数据方差；

2)建立混合高斯分布模型

混合高斯分布模型为多个高斯分布的线性组合，混合高斯分布其概率密度函数表示为

其中，X_COD,X_NH为进水COD量、进水氨氮量数据样本，a₁、a₂为进水COD量、进水氨氮量的高斯分布的权重。

步骤S303、基于非线性最小二乘法计算混合高斯分布模型系数，得到混合高斯分布函数。

1)根据进水COD量、进水氨氮量的历史数据信息，作为输入训练数据；

2)根据非线性最小二乘法，计算每个进水COD量和进水氨氮量的高斯分布模型系数，得到高斯分布的概率密度函数式；

其中，进水COD量高斯分布的概率密度函数为

进水氨氮量高斯分布的概率密度函数为

3)根据工况环境不同参数对设备运行控制的影响，为不同参数分配不同的影响因子系数；

其中，a₁＝1、a₂＝-0.1

4)根据工况环境不同参数的高斯分布的概率密度函数式和不同工况环境参数的影响因子系数，计算混合高斯分布模型系数，得到混合高斯分布函数。

步骤S304、根据混合高斯分布函数控制设备运行。

1)选取设备运行关键可调节参数指标，记为设备参数Y；

优选的是，本实施例中选择鼓风机频率作为设备关键可控参数指标；

2)构建设备参数Y与工况环境参数混合高斯分布概率间的关系，表达式为

其中，X′为设备运行的当前工况环境参数的数据信息，Y_max为设备运行中设备参数可调节的范围上限值，Y_min为设备参数可调节范围下限值，f(X)为工况参数混合高斯分布函数；

优选的是，本实施例中Y_max＝50Hz，Y_min＝30Hz；

3)通过数据采集设备，获取当前工况环境参数的数据信息值，进水COD量为230g/h，进水氨氮量为20g/h，即当前工况环境参数数据为X′＝(230,20)；

4)根据所述公式(13)和设备运行的当前工况环境参数的数据信息X′＝(230,20)，计算得到设备参数Y(X′)；

5)控制鼓风机以Y(X′)运行，即以40Hz运行。

注意，上述仅为本发明的较佳实施例及所运用技术原理。本领域技术人员会理解，本发明不限于这里所述的特定实施例，对本领域技术人员来说能够进行各种明显的变化、重新调整和替代而不会脱离本发明的保护范围。因此，虽然通过以上实施例对本发明进行了较为详细的说明，但是本发明不仅仅限于以上实施例，在不脱离本发明构思的情况下，还可以包括更多其他等效实施例，而本发明的范围由所附的权利要求范围决定。