一种基于双停泊轨道的Walker星座部署方法与流程

本发明涉及一种星座部署方法，尤其涉及一种基于双停泊轨道的Walker星座部署方法。

背景技术：

轨道通信系统(Orbcomm系统)属于专用数据通信卫星系统，是美国轨道通信公司(Orbcomm LLC)于世纪90年开始建设运营的短数据通信星座系统，Orbcomm系统卫星星座由47颗卫星组成，包括7个轨道面，采用轨道高度低于1000km的LEO轨道，Orbcomm星座部署采用一箭多星部署一个轨道面，7个轨道面需要发射7枚火箭。

铱星通信星座、全球星通信星座、GPS导航卫星星座以及北斗导航卫星星座等卫星星座系统均是利用一箭多星部署一个轨道面的卫星，在卫星质量轻的情况下，如微小卫星，这种部署方法需采用多枚火箭进行异面部署，系统发射部署成本高。

COSMIC星座为美国和台湾地区联合研制的掩星大气探测星座，由6颗卫星组成，分布于6个轨道面，即每个轨道部署1颗卫星；该COSMIC星座于2006年一箭6星发射部署，采用一箭多星发射单停泊轨道异面部署的方法，6颗卫星首先进入500km左右的低停泊轨道，此后每颗卫星到达预定轨道面时，依靠自身轨道机动能力进入轨道高度为800km左右的任务轨道。

以上说的这些现有卫星星座系统或相关专利文献提出的星座部署方法，存在以下几项缺点中的一点或几点：第一、一箭多星只部署一个轨道面，多个轨道面需多次发射，发射部署准备周期长、成本高，对于单轨道面数量少、卫星质量轻的星座，发射部署效费比低；如Orbcomm星座、铱星星座、全球星星座、GPS导航卫星星座和北斗卫星星座采用这种发射部署方式，但上述星座一个轨道面卫星数量较多或卫星质量重，一箭部署一个轨道面有其合理性。第二、一箭多星发射，利用单停泊轨道实现异面部署，可以解决一箭多星只部署一个轨道所带来的局限性，COSMIC星座部署采用这种方法；但在卫星数量较多且轨道面分布范围较大的情况下，利用一箭多星单停泊轨道实现异面部署，周期较长。

技术实现要素：

本发明所要解决的技术问题是需要提供一种能够解决一箭多星部署单轨道面的局限，并同时解决一箭多星单停泊轨道异面部署周期较长的缺点的Walker星座部署方法。

对此，本发明提供一种基于双停泊轨道的Walker星座部署方法，包括以下步骤：

步骤S1，将用于部署Walker星座的卫星分别依次送入第一停泊轨道和第二停泊轨道；

步骤S2，第一颗卫星通过轨道机动进入工作轨道，其余卫星停留在第一停泊轨道和第二停泊轨道；

步骤S3，等待当前停泊轨道的轨道面相对于相邻一颗卫星所在工作轨道的轨道面进动直到其升交点赤经相差预设角度时，下一颗卫星通过轨道机动进入工作轨道；依此直到用于部署Walker星座的所有卫星依次进入工作轨道。

本发明的进一步改进在于，所述步骤S2中，第一颗卫星通过轨道机动自第一停泊轨道进入工作轨道；

所述步骤S3包括以下子步骤：

步骤S301，等待第二停泊轨道的轨道面相对于相邻的第一颗卫星所在工作轨道的轨道面进动直到其升交点赤经相差预设角度时，第二颗卫星通过轨道机动自第二停泊轨道进入工作轨道；

步骤S302，等待第一停泊轨道的轨道面相对于第一停泊轨道中在先一颗卫星所在工作轨道的轨道面进动，直到其升交点赤经相差预设角度时，第三颗卫星通过轨道机动自第一停泊轨道进入工作轨道；等待第二停泊轨道的轨道面相对于第二停泊轨道中在先一颗卫星所在工作轨道的轨道面进动，直到其升交点赤经相差预设角度时，第四颗卫星通过轨道机动自第二停泊轨道进入工作轨道；依此循环运行所述步骤S302，直到用于部署Walker星座的所有卫星依次进入工作轨道。

本发明的进一步改进在于，所述第一停泊轨道的轨道高度高于工作轨道的轨道高度，所述第二停泊轨道的轨道高度低于工作轨道的轨道高度。

本发明的进一步改进在于，所述预设角度为360°/用于部署Walker星座的卫星数量。

本发明的进一步改进在于，不同高度的当前停泊轨道的轨道面相对于相邻一颗卫星所在工作轨道的轨道面的进动速率差计算公式为

其中，a₀为卫星工作轨道标称半长轴，e₀为卫星工作轨道标称偏心率，i₀为卫星工作轨道标称倾角，J₂为地球的非球形引力，μ为地球引力常数，R_e为地球参考半径，a为当前的停泊轨道半长轴；并根据轨道面升交点经度差及部署时间需求公式求得当前的停泊轨道半长轴a，其中，ΔΩ为当前的停泊轨道的轨道面与工作轨道的轨道面之间的升交点赤经，t为卫星在停泊轨道上的驻留时间。

本发明的进一步改进在于，用于部署Walker星座的卫星数量为六颗，所述步骤S1中三颗卫星送入第一停泊轨道，另外三个卫星送入第二停泊轨道；所述预设角度为60°。

本发明的进一步改进在于，设为工作轨道的升交点赤经进动速率，为第二停泊轨道的升交点赤经进动速率，为第一停泊轨道的升交点赤经进动速率，则其中，和这三个进动速率可以通过公式得到。

本发明的进一步改进在于，用于部署Walker星座的六颗卫星分别为A卫星、B卫星、C卫星、D卫星、E卫星和F卫星，所述步骤S1中，所述A卫星、B卫星和C卫星分别依次送入第二停泊轨道，所述D卫星、E卫星和F卫星分别依次送入第一停泊轨道；则所述Walker星座的部署过程如下：

步骤A，自入轨t_D天后，D卫星首先通过降轨进入工作轨道，t_D为D卫星部署完成所需时间；

步骤B，自入轨t_A天后，第二停泊轨道的轨道面相对D卫星工作轨道的轨道面升交点赤经差异达到60°，A卫星升轨至工作轨道，t_A为A卫星部署完成所需时间；

步骤C，自D卫星降轨t_E天后，第一停泊轨道的轨道面相对D卫星工作轨道面升交点赤经差异达到60°，E卫星降轨至工作轨道，t_E为E卫星部署完成所需时间；

步骤D，自A卫星升轨t_B天后，第二停泊轨道的轨道面相对A卫星工作轨道面升交点赤经差异达到60°，B卫星升轨至工作轨道，t_B为B卫星部署完成所需时间；

步骤E，自E卫星降轨t_F天后，第一停泊轨道的轨道面相对E卫星工作轨道面升交点赤经差异达到60°，F卫星降轨至工作轨道，t_F为F卫星部署完成所需时间；

步骤F，自B卫星升轨t_C天后，第二停泊轨道的轨道面相对B卫星工作轨道面升交点赤经差异达到60°，C卫星升轨至工作轨道，t_C为C卫星部署完成所需时间。

本发明的进一步改进在于，A卫星部署完成所需时间为D卫星部署完成所需时间为其中，Δt为预先设置好的隔离时间，该隔离时间用于避免出现两颗卫星在同一时期进行轨道机动。

本发明的进一步改进在于，E卫星部署完成所需时间公式为其中，为E卫星所在停泊轨道升交点赤经进动速率；B卫星部署完成所需时间公式为其中，为B卫星所在停泊轨道升交点赤经进动速率；F卫星部署完成所需时间公式为其中，为F卫星所在停泊轨道升交点赤经进动速率；C卫星部署完成所需时间公式为其中，为C卫星所在停泊轨道升交点赤经进动速率。E卫星所在停泊轨道、B卫星所在停泊轨道以及C卫星所在停泊轨道指的就是第一停泊轨道和第二停泊轨道。

与现有技术相比，本发明的有益效果在于：采用异面卫星星座部署方法实现一箭多星发射，并利用第一停泊轨道和第二停泊轨道的双停泊轨道实现异面部署，可以解决一箭多星部署单轨道面的局限，同时解决一箭多星单停泊轨道异面部署周期较长的缺点；在此基础上，本发明优化了星座部署时间和卫星与卫星之间相对位置的部署精度角度，提出将卫星从第一停泊轨道和第二停泊轨道依次送至工作轨道的机动策略。

附图说明

图1是本发明一种实施例的工作流程结构示意图；

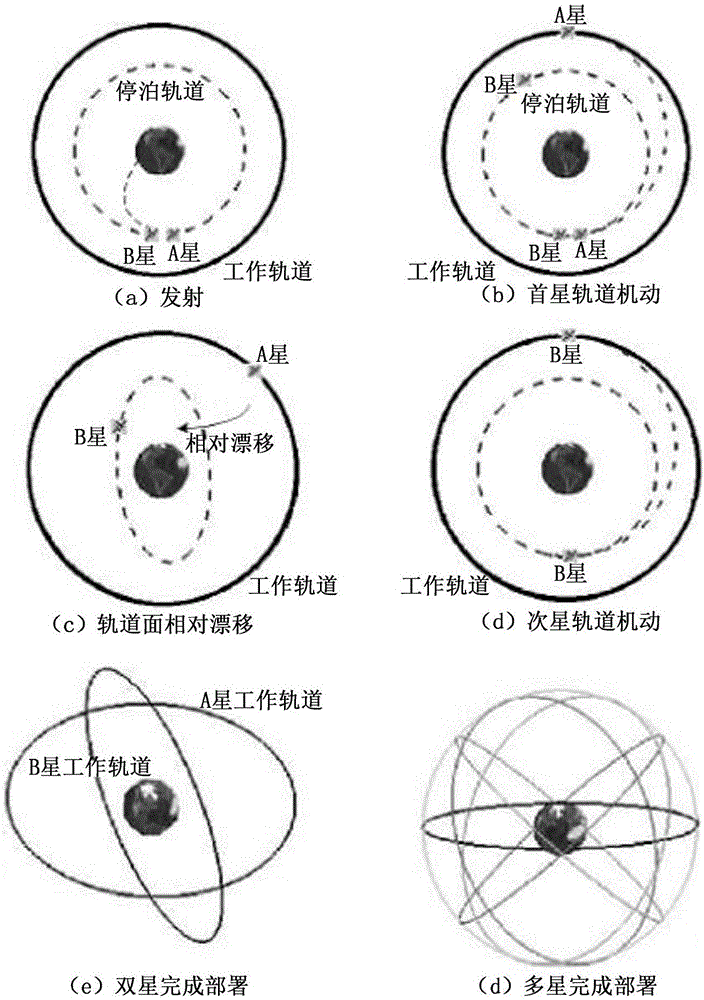
图2是本发明一种实施例的星座部署原理示意图；

图3是本发明一种实施例的星座部署时序原理示意图。

具体实施方式

下面结合附图，对本发明的较优的实施例作进一步的详细说明：

如图1所示，本例提供一种基于双停泊轨道的Walker星座部署方法，包括以下步骤：

步骤S1，将用于部署Walker星座的卫星分别依次送入第一停泊轨道和第二停泊轨道；

步骤S2，第一颗卫星通过轨道机动进入工作轨道，其余卫星停留在第一停泊轨道和第二停泊轨道；

步骤S3，等待当前停泊轨道的轨道面相对于相邻一颗卫星所在工作轨道的轨道面进动直到其升交点赤经相差预设角度时，下一颗卫星通过轨道机动进入工作轨道；依此直到用于部署Walker星座的所有卫星依次进入工作轨道。

本例所述第一停泊轨道的轨道高度优选高于工作轨道的轨道高度，所述第二停泊轨道的轨道高度优选低于工作轨道的轨道高度。所述预设角度一般设置为360°/用于部署Walker星座的卫星数量。

所述第一停泊轨道和第二停泊轨道统称为停泊轨道，即停泊轨道包括第一停泊轨道和第二停泊轨道；停泊轨道的用途类似于辅助车道，以此为跳板最终实现卫星进入设计工作轨道。本例所述双停泊轨道包括一个高于工作轨道的第一停泊轨道，另一个低于工作轨道的第二停泊轨道，这样设计的好处是使得“运行在高于工作轨道的第一停泊轨道上的卫星”与“运行在低于工作轨道的第二停泊轨道上的卫星”轨道升交点朝着相反方向进动，以此来实现轨道面之间的设计相位。

本例所述的高于工作轨道和低于工作轨道的限制范围相对宽松，其主要受到以下几个方面的约束：一、卫星自身速度增量的约束，变轨消耗的燃料不能过多，要保证轨道进动；二、部署时间约束，低地球轨道卫星设计寿命一般较短，过长的部署时间将增加星座构建风险以及星座系统的效能和实用性；三、轨道摄动的约束，第二停泊轨道高度不能过低，否则大气阻力影响多大，卫星需消耗多余的燃料用于维持轨道高度，对于需要长时间运行于停泊轨道的卫星尤其如此。此外，摄动力引起的轨道倾角差异和星间相对相位差异等也是需要考虑的问题。

本例的设计思路是：利用地球J2项非球形引力引起的轨道面进动实现星座的异面部署；对于地球卫星轨道，J2项非球形引力造成的升交点赤经进动速率为该公式中，为卫星所在轨道面升交点赤经进动速率，单位为rad/s；J₂为地球J₂项的非球形引力，无量纲，常取：J₂＝0.00108263；μ为地球引力常数，单位为km³/s²，常取μ＝398600.5km³/s²；a为卫星轨道半长轴，单位为km；R_e为地球参考半径，单位为km，常取：R_e＝6378.14km；e为卫星轨道偏心率，无量纲；i为卫星轨道倾角，单位为deg。

由上式可知，在轨道偏心率e、轨道倾角i一定的情况下，轨道面升交点赤经进动速率随半长轴的变化而变化，即不同卫星之间轨道高度的差异将引起卫星轨道面升交点赤经漂移速率的差异，进而实现星座的异面部署。

如图2所示，所述Walker星座基本部署过程如下：(1)通过运载火箭等将卫星依次送入轨道高度低于或高于工作轨道的第二停泊轨道或第一停泊轨道；(2)第一颗卫星首先通过轨道机动进入工作轨道，其余卫星停留在停泊轨道；(3)由于轨道面进动速率差异，停泊轨道面相对首颗卫星的工作轨道面进动；(4)当停泊轨道面进动至与相邻卫星的工作轨道面升交点赤经相差约60°时，第二颗卫星通过轨道机动进入工作轨道，其余卫星通过这种方式依次进入预期工作轨道。

也就是说，所述步骤S2中，第一颗卫星通过轨道机动自第一停泊轨道进入工作轨道；

所述步骤S3包括以下子步骤：

步骤S301，等待第二停泊轨道的轨道面相对于相邻的第一颗卫星所在工作轨道的轨道面进动直到其升交点赤经相差预设角度时，第二颗卫星通过轨道机动自第二停泊轨道进入工作轨道；

步骤S302，等待第一停泊轨道的轨道面相对于第一停泊轨道中在先一颗卫星所在工作轨道的轨道面进动，直到其升交点赤经相差预设角度时，第三颗卫星通过轨道机动自第一停泊轨道进入工作轨道；等待第二停泊轨道的轨道面相对于第二停泊轨道中在先一颗卫星所在工作轨道的轨道面进动，直到其升交点赤经相差预设角度时，第四颗卫星通过轨道机动自第二停泊轨道进入工作轨道；依此循环运行所述步骤S302，直到用于部署Walker星座的所有卫星依次进入工作轨道。

根据近地轨道进动规律，不同高度的当前停泊轨道的轨道面相对于相邻一颗卫星所在工作轨道的轨道面的进动速率差计算公式为

其中，a₀为卫星工作轨道标称半长轴，e₀为卫星工作轨道标称偏心率，i₀为卫星工作轨道标称倾角，J₂为地球的非球形引力，μ为地球引力常数，R_e为地球参考半径，a为当前的停泊轨道半长轴；并根据轨道面升交点经度差及部署时间需求公式求得当前的停泊轨道半长轴a，其中，ΔΩ为当前的停泊轨道的轨道面与工作轨道的轨道面之间的相对升交点赤经，t为卫星在停泊轨道上的驻留时间。

本例以用于部署Walker星座的卫星数量为六颗为优选实施例，所述步骤S1中三颗卫星送入第一停泊轨道，另外三个卫星送入第二停泊轨道；所述预设角度为60°，由于设计星座相邻轨道面之间的升交点赤经间隔为60°，停泊轨道(包括第一停泊轨道和第二停泊轨道)的轨道面进动至与相邻工作轨道的轨道面升交点赤经相差约60°时意味着运行在当前的停泊轨道(包括第一停泊轨道和第二停泊轨道)上的卫星完成了轨道调整。此时，当前的停泊轨道(包括第一停泊轨道和第二停泊轨道)上的卫星需变轨进入工作轨道。

在轨道偏心率e和轨道倾角i一定的情况下，轨道面升交点进动速率随半长轴的变化而变化，即不同卫星之间轨道高度的差异将引起卫星轨道面升交点进动速率的差异，可以此来实现星座的异面部署。假设为工作轨道的升交点赤经进动速率，单位为rad/s；为第二停泊轨道的升交点赤经进动速率，单位为rad/s；为第一停泊轨道的升交点赤经进动速率，单位为rad/s；则

因而，随着时间的积累，运行在第二停泊轨道上的卫星就与运行在第一停泊轨道上的卫星产生了明显的升交点赤经差异，当这个差异达到60°后部署一颗位于第一停泊轨道或第二停泊轨道上的卫星进入工作轨道；当这个差异达到120°时部署下一颗位于第二停泊轨道或第一停泊轨道上的卫星进入工作轨道；当这个差异达到180°时部署下一颗位于第一停泊轨道或第二停泊轨道上的卫星进入工作轨道；当这个差异达到240°时部署下一颗位于第二停泊轨道或第一停泊轨道上的卫星进入工作轨道；当这个差异达到300°时部署下一颗位于第一停泊轨道或第二停泊轨道上的卫星进入工作轨道。由于第一颗卫星作为基准星进入工作轨道，故升交点赤经差异达到300°后星座即可部署完成。也就是说，等待当前停泊轨道的轨道面相对于相邻一颗卫星所在工作轨道的轨道面进动直到其升交点赤经相差预设角度时，下一颗卫星通过轨道机动自另一个停泊轨道进入工作轨道；依此直到用于部署Walker星座的所有卫星依次进入工作轨道。

本例所述Walker星座优选共6颗卫星，根据任务要求，需将每颗卫星部署到6个不同的轨道面上。这6个轨道面均匀分布在360°升交点赤经上，相邻两个轨道面之间的升交点赤经间隔为60°。由于6颗卫星采用一箭6星的方式发射入轨，入轨后6星处于升交点赤经相近的轨道上。

本例用于部署Walker星座的六颗卫星分别为A卫星、B卫星、C卫星、D卫星、E卫星和F卫星，所述步骤S1中，所述A卫星、B卫星和C卫星分别依次送入第二停泊轨道，所述D卫星、E卫星和F卫星分别依次送入第一停泊轨道；如图3所示，则所述Walker星座的部署过程如下：

步骤A，自入轨t_D天后，D卫星首先通过降轨进入工作轨道，t_D为D卫星部署完成所需时间，其余卫星停留在各自的停泊轨道(包括第一停泊轨道和第二停泊轨道)；

步骤B，自入轨t_A天后，第二停泊轨道的轨道面相对D卫星工作轨道的轨道面升交点赤经差异达到60°，A卫星升轨至工作轨道，t_A为A卫星部署完成所需时间，届时A卫星和D卫星之间的轨道面升交点赤经相差60°，A卫星相位滞后D卫星240°；

步骤C，自D卫星降轨t_E天后，第一停泊轨道的轨道面相对D卫星工作轨道面升交点赤经差异达到60°，E卫星降轨至工作轨道，t_E为E卫星部署完成所需时间，届时D卫星和E卫星之间的轨道面升交点赤经相差60°，E卫星相位超前D卫星240°；

步骤D，自A卫星升轨t_B天后，第二停泊轨道的轨道面相对A卫星工作轨道面升交点赤经差异达到60°，B卫星升轨至工作轨道，t_B为B卫星部署完成所需时间，届时B卫星与A卫星之间的轨道面升交点赤经相差60°，B卫星相位滞后A卫星240°；

步骤E，自E卫星降轨t_F天后，第一停泊轨道的轨道面相对E卫星工作轨道面升交点赤经差异达到60°，F卫星降轨至工作轨道，t_F为F卫星部署完成所需时间，届时F卫星与E卫星之间的轨道面升交点赤经相差60°，F卫星相位超前E卫星240°；

步骤F，自B卫星升轨t_C天后，第二停泊轨道的轨道面相对B卫星工作轨道面升交点赤经差异达到60°，C卫星升轨至工作轨道，t_C为C卫星部署完成所需时间，届时C卫星与B卫星之间的轨道面升交点赤经相差60°，C卫星相位滞后B卫星240°。

经过以上描述，如图3所示，6颗卫星部署序列为D卫星→A卫星→E卫星→B卫星→F卫星→C卫星，轨道面自西向东排序为C卫星→B卫星→A卫星→D卫星→E卫星→F卫星，整个星座部署时序示意图如下图3所示。

本例所述Walker星座的星座部署时序示意图如图3所示，所述A卫星部署完成所需时间为D卫星部署完成所需时间为其中，Δt为预先设置好的隔离时间，该隔离时间用于避免出现两颗卫星在同一时期进行轨道机动。

所述E卫星部署完成所需时间为其中，为E卫星所在停泊轨道升交点赤经进动速率；B卫星部署完成所需时间为其中，为B卫星所在停泊轨道升交点赤经进动速率；F卫星部署完成所需时间为其中，为F卫星所在停泊轨道升交点赤经进动速率；C卫星部署完成所需时间为其中，为C卫星所在停泊轨道升交点赤经进动速率。

若不考虑初始入轨时间差异及升降轨所需时间，根据图3所示的星座部署时序示意图，第二停泊轨道的全部卫星完成升轨部署所需时间为t_L＝t_A+t_B+t_C；第一停泊轨道的全部卫星完成降轨部署所需时间为t_H＝t_D+t_E+t_F+Δt。卫星所在停泊轨道运行时间与相对升交点赤经存在以下关系式该公式中，ΔΩ_AD为初始时刻A卫星相对D卫星的升交点赤经之间的差值。为了使部署时间T取得最小值的t_A，其为

将t_A代入前式求得t_D为

在各卫星的停泊轨道参数为标称值的情况下，t_A求解式简化为t_D求解式简化为

根据霍曼变轨规律，从停泊轨道至工作轨道可以通过两次脉冲速度增量实现，单次速度增量及总速度增量分别为该公式中，ΔV₁为霍曼转移第一次脉冲所需速度增量，单位为km/s；ΔV₂为霍曼转移第二次脉冲所需速度增量，单位为km/s；ΔV为霍曼转移所需速度增量总和，单位为km/s；a为停泊轨道半长轴，单位为km；a₀为工作轨道半长轴，单位为km。

基准星部署轨道机动规划以星座总部署时间最优为目标，同时综合考虑部署机动时间、推进和测控等条件约束，权衡确定基准星降轨时机及降轨高度。星座部署包括基准星和非基准星的轨道机动部署。基准星的部署以星座部署所需时间为优化目标，基准星最佳降轨时机为

考虑工程实施约束，基准星的降轨过程尽量保证在测控圈内，离t_Dopt最近的时间点作为次优的升降轨时间点。非基准星部署轨道机动规划以相对相位最优且相对升交点经度次优为目标，确定部署机动日期及变轨量。升交点赤经偏差最小的首次部署机动日期为上式中，floor()为向下取整函数，如floor(5.6)＝5，floor(5.3)＝5；t₀为设定起始时刻；t_m-t₀之后第N天卫星实施首次部署机动，满足测控可见性及变轨点纬度幅角要求的时刻；Δu₀为t₀初始时刻相对目标部署相位的偏差，单位为rad；为非基准星相对基准星的轨道角速率，单位为rad/s。Δu_mr为升降轨期间累积的相对相位，其符号与k相同。k为整数，算式如下：ΔΩ₀为t₀初始时刻非基准星相对目标升交点赤经的偏差。p的算式如下：该公式中，J₂为地球非球形引力J₂带谐项系数。R_e为地球参考半径。a_o为基准星工作轨道半长轴，单位为km。i_o为基准星工作轨道倾角，单位为deg。c＝a_p/a_o，a_p为非基准星停泊轨道半长轴，无量纲。

在确定首次部署机动日期的情况下，根据测控及纬度幅角条件选定t_m由于实际变轨过程总是存在误差，当天的变轨量需对之前的累积相位偏差进行修正，以保证后续相位部署精度。设第d天机动之前每天相对基准星的实际累积相对相位为Δλ_i(i＝1...d-1,d＜6)，重新规划第d天相对基准星需累积的相位为

单位为rad/day，其中第d天轨道半长轴机动目标量为该公式中，t_in为当天霍曼转移第一次变轨时刻，根据卫星测控可见性具体选定；t_out为后一天霍曼转移第一次变轨时刻，根据卫星测控可见性具体选定；这两个时刻根据卫星测控可见性具体选定。n_o为基准星轨道角速率，rad^-1，按下式计算：

本例采用异面卫星星座部署方法实现一箭多星发射，并利用第一停泊轨道和第二停泊轨道的双停泊轨道实现异面部署，可以解决一箭多星部署单轨道面的局限，同时解决一箭多星单停泊轨道异面部署周期较长的缺点；在此基础上，本例优化了星座部署时间和卫星与卫星之间相对位置的部署精度角度，提出将卫星从第一停泊轨道和第二停泊轨道依次送至工作轨道的机动策略。

以上内容是结合具体的优选实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属技术领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干简单推演或替换，都应当视为属于本发明的保护范围。