一种FastRVM污水处理在线故障诊断方法与流程

本发明涉及污水处理领域，特别涉及一种FastRVM污水处理在线故障诊断方法。
背景技术：
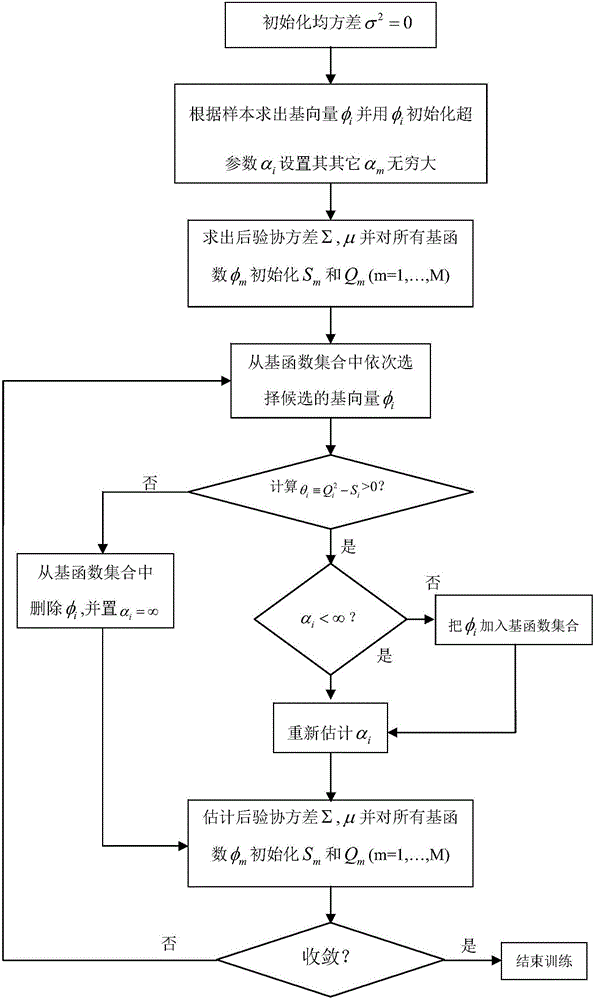
：目前，环境保护已经成为我国经济可持续发展的重要基础，随着我国工业经济发展迅速，城市进程不断加快，工业废水的排放量随着工业用水量的增加而快速增长，大部分废水的直接排放又严重污染了江河水体，破坏了生态平衡，间接的影响了人们的生活。污水处理厂作为自然水体的关键保护屏障，其运行好坏将直接影响水环境的安全程度。污水生化处理工艺复杂，影响因素非常多，污水处理厂在实际运行过程中难以保持长期稳定的运行，一旦发生运行故障常常会引起出水水质不达标、运行费用增高和环境二次污染等严重问题。因此，必须对污水处理厂运行状态进行监控，及时诊断出污水处理过程故障并予以处理。污水处理过程运行状态的故障诊断本质上是一个模式分类问题，而在实际状态运行分类中，常常会遇到污水数据集的分布不均衡问题，现有技术存在一定的局限性，在用于不平衡数据分类时，模型分类正确率无法满足要求，给污水生化处理的故障诊断带来了极大的困难；同时在实际过程当中，故障诊断实际上是一个连续的学习过程，其突出的一个特点就是学习不是一次离线进行的，而是数据逐一加入的，不断进行优化的过程。在线学习方法要求在获得下一个数据之前必须完成训练，否则会影响下一步决策的完成，而且污水处理厂的运行出现的故障信息尤为重要，所以在线故障诊断系统更加注重的是快速性和准确性。技术实现要素：本发明的目的在于克服现有技术的不足，提供一种基于不平衡数据聚类的FastRVM污水处理在线故障诊断方法，通过基于聚类的快速相关向量机方法对多数类数据压缩和虚拟少数类向上采样的方法对少数类数据扩充，降低了污水数据的不平衡性，提高分类准确率，同时采用FastRVM对污水生化处理过程建立多分类模型，加快在线更新速度，从而保证了污水处理过程的在线故障诊断的准率性和实时性。为实现上述目的，本发明所提供的技术方案为：一种FastRVM污水处理在线故障诊断方法，包括以下步骤：S1.剔除掉污水数据中属性不完整的样本，由于各输入变量量纲的不同，对其进行归一化处理，归一化到[0,1]区间中，并确定历史数据集xold和更新测试集xnew；S2.将历史数据中的多数类样本采用基于聚类的快速相关向量机方法进行压缩；S3.根据虚拟少数类向上采样的方法对历史数据中的少数类样本进行扩充；S4.将处理后的历史数据中所有类的样本数据重新组合构成新的历史训练集，并建立“一对一”的快速相关向量机多分类训练模型；S5.从更新测试集xnew中添加k个新样本到模型中进行测试，并保存分类测试结果，将其添加到历史数据集中，去掉历史数据集中前k个样本；S6.回到步骤S2，重新处理不平衡的历史数据，训练模型，不断重复上述过程，直到在线更新数据测试完毕，得到最终在线测试结果，从而实现对污水处理过程的在线运行状态的识别。所述的步骤S2，具体为：S201、假设多数类样本集X＝{x1,x2,…,xi,…,xn}为n个Rd空间的数据，其中d为样本属性的维数，从n个数据对象中随机选择k个对象作为初始的聚类中心；S202、然后对剩余的样本对象则根据与各个聚类中心的距离分别分配到距离最相近的聚类中心中；计算距离的公式如下，假设cj为第j个类的中心，则xi与cj的距离为：S203、根据集合中的点更新每个类的聚类中心，假设第j个类中的样本为即包含了nj个样本，则该类的聚类中心为其中为类中心cj的第m个属性，计算公式如下：S204、不断重复S202、S203步骤，直到标准测度函数收敛为止，采用均方差作为计算标准测度函数，其形式为：S205、将聚类后的多数类样本进行快速相关向量机分类建模，从而可以获取一定数量的相关向量，这些相关向量的个数要比原始多数类数据少得多，并且具有一定的代表性，接着用选取的相关向量代替原来的多数类样本从而对多数类样本的压缩。所述的步骤S3，具体为：S301、对少数类中的每一个样本x，以欧式距离为标准计算它到少数类样本集中每个样本的距离，获得其中k个最近邻，并记录近邻样本的下标；S302、根据向上采样的倍率N，对每一个少数类样本x，从其k个最近邻中随机选取N个样本，记为y1,y2,…,yN；S303、在原样本x与yj(j＝1,2,…,N)之间进行随机线性插值，构造新的少数类样本pj，即新样本：pj＝x+rand(0,1)*(yj-x),j＝1,2,…,N(4)其中rand(0,1)表示区间(0,1)内的一个随机数。步骤S4中，“一对一”的快速相关向量机多分类训练模型，其建立过程如下：处理后的历史数据及可以定义为其中N是数据集的样本个数,n是样本序号,d是样本属性的维数，zn为样本的输入，tn为样本的目标值，预测函数如公式一所示：tn＝y(zn；w)+εn(5)其中y(z)的定义如公式(2所示)其中K(z,zi)是核函数，wi为基函数对应的权重,w＝[w0,w1,…,wN]T,εn为噪声，服从εn～N(0,σ2)，因此tn～N(y(zn,w),σ2)。假设预测目标tn之间相互独立，那么就有：式中Φ是一个N×(N+1)的构造矩阵，为了避免过拟合，需要约束模型中的权值ω，假设其服从高斯分布，α为超参数。当输入一组新的变量的时候，对应的目标值t*为p(t*|t)～p(w,α,σ2|t)，根据先验概率分布和似然估计分布，可得权重的后验概率分布：p(ω,α,σ2|t)＝p(ω|t,α,σ2)p(α,σ2|t)(8)对上式进行近似处理，最终成了最大化p(α,σ2|t)∝p(t|α,σ2)p(α)p(σ2)的过程，也就是找到参数α和σ2最可能的值αMP、快速相关向量机在训练过程中从空集开始动态地扩充基矩阵Φ，从而增大边际似然函数，或者去掉基矩阵Φ冗余的列来增大目标函数。通过将边界似然函数p(t|α,σ2)取对数，记L(α)＝log[p(t|α,σ2)]，整理有：其中L(α-i)表示为当αi＝∞时，相应的基本向量φi被移除后所对应的边界似然函数的对数，而l(αi)表示边界似然的对数函数中只与αi有关的独立部分。Si被定义为稀疏因子，Qi为质量因子。L(α)有唯一最大值点为：为了最大化L(α)，根据公式(10),不断地迭代来寻找到合适的权重，这时超参数α也会对着权重w不断更新，通过不断地更新，可以得到最终的训练模型一些样本点对应的权重为零，那些不为零的点就是相关向量。综上所述，快速相关向量机分类基本算法步骤如下：(1)初始化σ2＝0；(2)用单个基向量φi初始化αi，由公式(10)分析整理可得并设置其他的αm(m≠i)为无穷大；(3)计算协方差矩阵Σ、权重矩阵μ并对所有M个基函数φm初始化Sm和Qm；(4)从所有M个基函数φm集合中选择候选的基向量φi；(5)计算(6)若θi＞0且αi＜∞，重新估计αi；(7)若θi＞0且αi＝∞，添加φi到模型中并重新估计αi；(8)若θi≤0且αi＜∞，删除φi并设置αi＝∞；(9)用Laplace逼近方法重新计算协方差矩阵Σ，权重矩阵μ以及相应迭代过程中的Sm和Qm；(10)若收敛或者达到最大迭代次数，则终止程序；否则转步骤(4)；终止条件为：任意在模型中的基函数对应的αi，有αi＜le12且建立完快速相关向量机的而分类模型后，再将多个二分类器采用“一对一”方法相结合，建立一个多分类器，设待分类样本为k个类别，这k类中的任意两类都可以组成一个基本的快速相关向量机二分类器，对所有的训练样本进行两两分类，这样k个类别两两之间共计可以构成个快速相关向量机二分类器，每一个快速相关向量机分类器只在各自对应的样本子集上进行训练。对未知样本进行分类测试时，采用投票的方法，把每一个待测样本都经过全部个分类器进行判别。例如，样本在i、j两类之间分类时，机器判别结果其属于第i类，就在第i类上增加1票，否则对第j类投票加1，直到所有的分类器分类完成，最后统计得票最多的类即为测试样本所属类别。设分类函数fij(x)用来判别i、j两类样本，若fij(x)＜0，则判别x属于第i类，记i类得1票，否则判x属于第j类，记j类得1票，最后决策时，比较哪一类得到的票最多，则将测试样本规划为该类。本发明与现有技术相比，具有如下优点与有益效果：1、本发明建立了一种基于不平衡数据聚类的FastRVM污水处理的在线故障诊断模型，通过基于聚类的快速相关向量机方法对多数类数据压缩和虚拟少数类向上采样方法对少数类数据扩充，降低了污水数据的不平衡性，同时采用FastRVM对污水生化处理过程建立多分类模型，加快在线更新速度，然后根据工况添加数据进行实时诊断并更新模型，等待下一次故障诊断，从而建立了在线故障诊断模型。该在线模型提高了对污水生化处理系统的故障诊断精度，在线性能好，效果显著。2、本发明的模型是基于聚类的快速相关向量机对多数类数据压缩和虚拟少数类向上采样方法对少数类数据扩充，降低了污水数据的不平衡性，不仅能够在平衡数据获得良好效果，而且还能够在不平衡数据取得比较好的分类效果，在此基础上采用了FastRVM建立的多分类器，其关键点在于它对训练样本的超参数进行快速估计，去除训练样本的非相关向量，保证模型的稀疏性，从而减少训练时间。因此，本发明采用的一种基于不平衡数据聚类的FastRVM污水处理的在线故障诊断方法对污水处理过程进行在线故障诊断建模，能够保证污水处理过程的在线故障诊断的准率性和实时性。3、本发明在线仿真实验时，需要对每一组新的数据进行测试并加入模型进行更新。历史数据集通过采取限定记忆的方式来保持其容量，使训练数据始终是有限组，每增加一组最新的观测数据，就随即丢弃一组最早的观测数据，从而保证模型中都包含新数据的信息，避免历史所含数据信息淹没新数据所包含的信息。附图说明图1为本发明模型基于不平衡数据聚类的FastRVM污水处理在线故障诊断方法流程图。图2为本发明模型快速相关向量机分类算法流程图。图3为本发明模型“一对一”的快速相关向量机多分类模型示意图。具体实施方式下面结合具体实施例对本发明作进一步详细的描述。如图1所示，本发明提供的FastRVM污水处理在线故障诊断方法，基于不平衡数据聚类，具体情况如下：S1.剔除掉污水数据中属性不完整的样本，由于各输入变量量纲的不同，对其进行归一化处理，归一化到[0,1]区间中，并确定历史数据集xold和更新测试集xnew；S2.将历史数据中的多数类样本采用基于聚类的快速相关向量机方法进行压缩；S3.根据虚拟少数类向上采样的方法对历史数据中的少数类样本进行扩充；S4.将处理后的历史数据中所有类的样本数据重新组合构成新的历史训练集，并建立“一对一”的快速相关向量机多分类训练模型；S5.从更新测试集xnew中添加k个新样本到模型中进行测试，并保存分类测试结果，将其添加到历史数据集中，去掉历史数据集中前k个样本；S6.回到步骤S2，重新处理不平衡的历史数据，训练模型，不断重复上述过程，直到在线更新数据测试完毕，得到最终在线测试结果，从而实现对污水处理过程的在线运行状态的识别。所述的步骤S2，具体为：S201、假设多数类样本集X＝{x1,x2,…,xi,…,xn}为n个Rd空间的数据，其中d为样本属性的维数，从n个数据对象中随机选择k个对象作为初始的聚类中心；S202、然后对剩余的样本对象则根据与各个聚类中心的距离分别分配到距离最相近的聚类中心中；计算距离的公式如下，假设cj为第j个类的中心，则xi与cj的距离为：S203、根据集合中的点更新每个类的聚类中心，假设第j个类中的样本为即包含了nj个样本，则该类的聚类中心为其中为类中心cj的第m个属性，计算公式如下：S204、不断重复S202、S203步骤，直到标准测度函数收敛为止，采用均方差作为计算标准测度函数，其形式为：S205、将聚类后的多数类样本进行快速相关向量机分类建模，从而可以获取一定数量的相关向量，这些相关向量的个数要比原始多数类数据少得多，并且具有一定的代表性，接着用选取的相关向量代替原来的多数类样本从而对多数类样本的压缩。所述的步骤S3，具体为：S301、对少数类中的每一个样本x，以欧式距离为标准计算它到少数类样本集中每个样本的距离，获得其中k个最近邻，并记录近邻样本的下标，这里k取5；S302、根据向上采样的倍率N，对每一个少数类样本x，从其k个最近邻中随机选取N个样本，记为y1,y2,…,yN；S303、在原样本x与yj(j＝1,2,…,N)之间进行随机线性插值，构造新的少数类样本pj，即新样本：pj＝x+rand(0,1)*(yj-x),j＝1,2,…,N(14)其中rand(0,1)表示区间(0,1)内的一个随机数。步骤S4中，“一对一”的快速相关向量机多分类训练模型，如图3所示，其建立过程如下：处理后的历史数据及可以定义为其中N是数据集的样本个数,n是样本序号,d是样本属性的维数，zn为样本的输入，tn为样本的目标值，预测函数如公式一所示：tn＝y(zn；w)+εn(15)其中y(z)的定义如公式(2所示)其中K(z,zi)是核函数，wi为基函数对应的权重,w＝[w0,w1,…,wN]T,εn为噪声，服从εn～N(0,σ2)，因此tn～N(y(zn,w),σ2)。假设预测函数tn之间相互独立，那么就有：式中Φ是一个N×(N+1)的构造矩阵，为了避免过拟合，需要约束模型中的权值ω，假设其服从高斯分布，α为超参数。当输入一组新的变量的时候，对应的目标值t*为p(t*|t)～p(w,α,σ2|t)，根据先验概率分布和似然估计分布，可得权重的后验概率分布：p(ω,α,σ2|t)＝p(ω|t,α,σ2)p(α,σ2|t)(18)对上式进行近似处理，最终成了最大化p(α,σ2|t)∝p(t|α,σ2)p(α)p(σ2)的过程，也就是找到参数α和σ2最可能的值αMP、快速相关向量机在训练过程中从空集开始动态地扩充基矩阵Φ，从而增大边际似然函数，或者去掉基矩阵Φ冗余的列来增大目标函数。通过将边界似然函数p(t|α,σ2)取对数，记L(α)＝log[p(t|α,σ2)]，整理有：其中L(α-i)表示为当αi＝∞时，相应的基本向量φi被移除后所对应的边界似然函数的对数，而l(αi)表示边界似然的对数函数中只与αi有关的独立部分。Si被定义为稀疏因子，Qi为质量因子。L(α)有唯一最大值点为：为了最大化L(α)，根据公式(20),不断地迭代来寻找到合适的权重，这时超参数α也会对着权重w不断更新，通过不断地更新，可以得到最终的训练模型一些样本点对应的权重为零，那些不为零的点就是相关向量。如图2所示，快速相关向量机分类基本算法步骤如下：(1)初始化σ2＝0；(2)用单个基向量φi初始化αi，由公式(20)分析整理可得并设置其他的αm(m≠i)为无穷大；(3)计算协方差矩阵Σ、权重矩阵μ并对所有M个基函数φm初始化Sm和Qm；(4)从所有M个基函数φm集合中选择候选的基向量φi；(5)计算(6)若θi＞0且αi＜∞，重新估计αi；(7)若θi＞0且αi＝∞，添加φi到模型中并重新估计αi；(8)若θi≤0且αi＜∞，删除φi并设置αi＝∞；(9)用Laplace逼近方法重新计算协方差矩阵Σ，权重矩阵μ以及相应迭代过程中的Sm和Qm；(10)若收敛或者达到最大迭代次数，则终止程序；否则转步骤(4)；终止条件为：任意在模型中的基函数对应的αi，有αi＜le12且建立完快速相关向量机的而分类模型后，再将多个二分类器采用“一对一”方法相结合，建立一个多分类器，设待分类样本为k个类别，这k类中的任意两类都可以组成一个基本的快速相关向量机二分类器，对所有的训练样本进行两两分类，这样k个类别两两之间共计可以构成个快速相关向量机二分类器，每一个快速相关向量机分类器只在各自对应的样本子集上进行训练。对未知样本进行分类测试时，采用投票的方法，把每一个待测样本都经过全部个分类器进行判别。例如，样本在i、j两类之间分类时，机器判别结果其属于第i类，就在第i类上增加1票，否则对第j类投票加1，直到所有的分类器分类完成，最后统计得票最多的类即为测试样本所属类别。设分类函数fij(x)用来判别i、j两类样本，若fij(x)＜0，则判别x属于第i类，记i类得1票，否则判x属于第j类，记j类得1票，最后决策时，比较哪一类得到的票最多，则将测试样本规划为该类。下面我们结合具体数据对本发明上述的加权极限学习机污水处理在线故障诊断方法进行具体说明，如下：实验仿真的数据来自UCI数据库，是一个污水处理厂的两年内的日常监控数据，整个数据集包括不完整记录在内一共有527个记录，每个样本维数为38(即38个测量变量，对应各个指标的值)，全部属性值都完整的记录有380个，被监测的水体一共有13种状态，各个状态用数字代替(为方便起见省去状态称)。527个记录在13种状态下的分布情况见下表1。表1-527个记录在13种状态下的分布情况类别12345678910111213个数2791141163116515311为了简化分类的复杂度，我们根据样本类别的性质，将样本分为4大类，如下表2。表2-527个记录在4种状态下的分布情况类别1234个数3321166514类别1为正常情况，类别2为性能超过平均值的正常情况，类别3为进水流量低的正常情况，类别4为二沉池故障、暴雨引起的非正常状态和固体溶度过负荷等原因引起的故障情况。本实施例上述的基于不平衡数据聚类的FastRVM污水处理的在线故障诊断方法，包含以下顺序的步骤：S1.首先剔除掉527个污水数据中147个属性不完整的数据，得到380个属性完整数据，然后将数据按式归一化处理，将处理后的数据集按2:1的比例进行随机分层抽样，得到历史数据集xold和在线更新测试集xnew。S2.将历史数据集中的多数类样本(第一类)提取出来，采用K-means方法将其聚成两类，然后将聚类后的第一类数据采用快速相关向量机方法进行建模，得到合适数量的相关向量，用所选取的相关向量代替多数类样本；S3.根据向上采样的倍率，采用虚拟少数类向上采样的方法将历史样本中的少数类样本(第三类和第四类)进行扩；S4.将处理后的所有类的历史样本数据重新组合构成新的历史训练集，如表3所示，建立“一对一”的快速相关向量机多分类训练模型。多分类训练模型选用RBF核函数，核宽度参数通过对新的训练集采用5折交叉验证的网格搜索方法来确定，然后根据总共有四个类别，一共建立6个二分类器；S5.从在线更新测试集xnew中取k个新样本到多分类器模型中进行测试，对6个分类器分别输入测试集xnew，进行投票，保存分类测试结果，将其添加到历史数据集中，去掉历史数据集中前k个样本；S6.回到步骤S2，重新训练模型，不断重复上述过程，直到在线更新数据测试完毕，得到最终在线测试结果，从而实现对污水处理过程的在线运行状态的识别。本发明所采用的基于聚类的FastRVM污水处理在线故障诊断模型能够很好的满足要求，从而实现对污水处理过程运行状态的实时监测与控制，值得推广。表2-527个记录在4种状态下的分布情况以上所述之实施例子只为本发明之较佳实施例，并非以此限制本发明的实施范围，故凡依本发明之形状、原理所作的变化，均应涵盖在本发明的保护范围内。当前第1页1 2 3