一种存在测量不确定性下的反馈路径规划方法与流程

本发明属于路径规划与动力学控制领域，涉及一种存在测量不确定性下的反馈路径规划方法。

背景技术：

复杂环境下的路径规划算法研究由来已久，已经有很多方法可以实现，比如APF算法，PRM算法，RRT算法。但是传统的算法在动力学层面上并不能真实保证安全轨迹的运行，因此又诞生了一些考虑动力学因素的路径规划算法比如。MIT的EECS实验室的Russ Tedrake教授提出采用LQR-trees方法。这种方法类似于IHMPC方法，在局部计算线性反馈控制，采用路径规划算法RRT将局部稳定控制扩展到全局，从而实现全局稳定控制。

由于求取反馈控制吸引域需要复杂的凸优化方法：sums of squares，因此计算速度缓慢，A.Majumdar采用离线计算局部路径的算法，然后在线进行整合优化，求解全局路径。并将动力学系统的不确定性考虑到整个算法中，最终形成具有一定鲁棒性的路径规划算法。

技术实现要素：

本发明针对反馈路径规划中存在干扰和测量不确定性问题，考虑测量和系统误差，提供一种采用庞德里亚金集差的存在测量不确定性下的反馈路径规划方法。

为达到上述目的，本发明采用以下技术方案予以实现：

一种存在测量不确定性下的反馈路径规划方法，包括以下步骤：

1)开环轨迹计算：

开环轨迹计算采用PRM算法进行计算，然后采用PRM离散点作为初始估计；

2)计算局部反馈吸引域：

采用SOS算法进行计算，得到高阶较大的吸引域；

考虑一般非线性动力学系统：

假设开环轨迹和开环控制采用x₀,u₀表示，将坐标转变换到局部坐标系：

假设吸引域中初始状态满足x₀(0)∈χ₀，在时间区间t∈[0,T]中，存在集合满足：

定义：集合是参数化以后的吸引域的子集，其满足：

使得

采用SOS计算吸引域，假设局部吸引域的估计表示为：

其中S_i＝S_i^T，因此

求解时变黎卡提方程：得到每一时刻lyapunov函数的表达式；这个lyapunov函数作为SOS求解吸引域的初始估计：

3)计算误差椭圆：

定义：椭圆ε(q,Q)表示q为椭圆圆心，且<>表示内积；

首先将非线性系统离散化：

其中w_k和v_k+1分别为系统噪声和观测噪声；标称系统为：

x_0k+1＝f(x_0k)+B_ku_0k (8)

通过LQR算法得到局部反馈系数K_k得到控制律：

假设为实际值与估计值的误差，e^e∈ε(0,P_k)，Pk为后验误差估计，ε(·)表示椭圆；后验估计误差采用ESMF、EKF或者其他滤波算法得到；假设为估计状态和标称状态的误差；

令所以实际状态表示为：

因此有：

其中：

A_G＝A_k+B_kK_k，

因此标称估计的预测值：其中椭圆参数：

4)在线计算：

离线计算得到吸引域，采用GP进行在线估计，采用GPML工具箱进行计算，得到估计吸引与上界ρ，从而形成吸引与椭圆E(t_i)，与误差椭圆进行庞德里亚金集差；得到新的标称轨迹附近的吸引域。

本发明进一步的改进在于：

步骤1)采用GPOPS-II软件进行非线性轨迹计算。

步骤2)中，求解吸引域的具体方法如下：

2-1)初始化LQR反馈控制得到的lyapunov函数V和初始猜测值ρ(t)；

2-2)初始先验指标函数为正无穷，即cost_prev＝∞，且当前状态不收敛；

2-4)如果不收敛，开始循环：

a.最小化函数：固定V和ρ(t)找(L,L_t,L_0,i,L_E,i)与S_i；

b.最小化函数：固定L,L_E,i找(V,ρ,L_t,L_0,iS_i)；

2-5)令当前指标函数

2-6)如果则收敛，结束如果；

2-7)先验指标等于当前指标：cost_prev＝cost；

2-8)结束循环；

其中，L,L_t,L_0,i,L_E,i均为拉格朗日乘子，为状态量x的函数，系数待定；ε为预设一小实数。

步骤4)的具体方法如下：

4-1)初始化并构建地图；

4-2)采用PRM算法进行初始路径估计，得到可行路径；

4-3)基于步骤4-2)中PRM方法得到初始路径参考值，采用GPOPS-II计算开环路经与开环控制律；

4-4)采用时变黎卡提方程计算初始lyapunov函数；

4-5)开始循环；

4-6)获取当前状态估计值；

4-7)采用GP方法估计吸引域半径，训练数据来源于吸引域的离线计算；

4-8)检查误差椭圆与吸引域椭圆距离，如果小于吸引域椭圆半径，则采用庞德里亚金集差方法计算新的鲁棒吸引域，具体为吸引域椭圆与误差椭圆做差；否则回到步骤4-2)重规划；

4-9)检查当前鲁棒吸引域与障碍物是否无碰撞，如果碰撞则增加GPOPS-II的约束升级开环控制u₀；

4-10)结束循环。

与现有技术相比，本发明具有以下有益效果：

本发明考虑测量不确定性对于反馈吸引域的影响，采用庞德里亚金集差缩小了吸引域的大小，重新评估路径规划过程中的安全避障问题，并采用GP算法在线估计吸引域大小从而克服吸引域计算缓慢的缺陷。本发明重新修正局部反馈控制吸引域的大小，并在线进行路径规划的算法。本发明考虑测量不确定性对标称轨迹的影响，对吸引域进行重新修正，形成更小且更安全的吸引域，从而保证路径规划的快速性和安全性。

【附图说明】

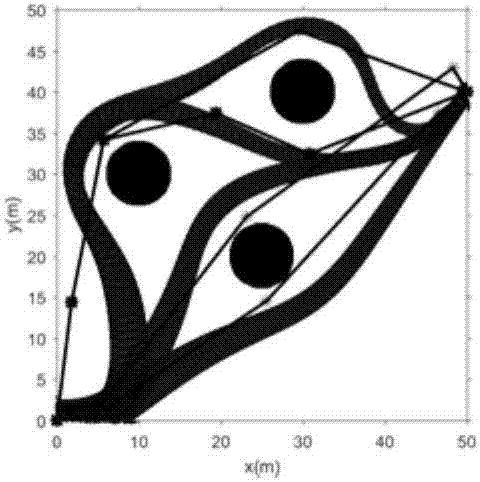
图1为PRM路径与NLP避障路线的示意图；

图2为高斯估计离线数据库的示意图；

图3为测量缺失无法运行到目标的示意图；

图4为具有测量时可以到达目标的示意图；

图5为安全路径1的示意图；

图6为安全路径2的示意图。

【具体实施方式】

下面结合附图对本发明做进一步详细描述：

参见图1-6

步骤一、开环轨迹计算

开环轨迹计算采用PRM算法进行计算，然后采用PRM离散点作为初始估计，将问题转化为一个非线性规划的问题，从而采用非线性规划算法进行开环轨迹控制计算。本发明的实施实例采用GPOPS-II软件进行非线性轨迹计算。

步骤二、计算局部反馈吸引域

吸引域的算法很多，本发明的实施实例采用SOS(sums of squares)算法进行计算，可以得到高阶较大的吸引域。

考虑一般非线性动力学系统：

假设步骤一中的开环轨迹和开环控制采用x₀,u₀表示，将坐标转变换到局部坐标系：

假设吸引域中初始状态满足x₀(0)∈χ₀，在时间区间t∈[0,T]中，存在集合满足：

定义：集合是参数化以后的吸引域的子集，其满足：

使得

采用SOS计算吸引域，假设局部吸引域的估计可以表示为：

其中S_i＝S_i^T，因此

求解时变黎卡提方程：得到每一时刻lyapunov函数的表达式。这个lyapunov函数作为SOS求解吸引域的初始估计：

因此求解吸引域算法具体如下：

算法1：

步骤三、计算误差椭圆

定义：椭圆ε(q,Q)表示q为椭圆圆心，且(<>表示内积)。

首先将非线性系统离散化：

其中w_k和v_k+1分别为系统噪声和观测噪声。标称系统为：

x_0k+1＝f(x_0k)+B_ku_0k (8)

通过LQR算法得到局部反馈系数K_k得到控制律：

假设为实际值与估计值的误差，e^e∈ε(0,P_k)，P_k为后验误差估计，ε(·)表示椭圆。后验估计误差可以采用ESMF或者EKF以及其他滤波算法得到。假设为估计状态和标称状态的误差。

令所以实际状态可以表示为：

因此有：

其中：A_G＝A_k+B_kK_k，因此标称估计的预测值：其中椭圆参数：

步骤四、在线计算

离线计算得到吸引域(见步骤一)，采用GP(Gaussian Process Regression)进行在线估计，本发明采用GPML工具箱进行计算，得到估计吸引与上界ρ。从而形成吸引与椭圆E(t_i)，与误差椭圆进行庞德里亚金集差(Pontryagin Difference)。得到新的标称轨迹附近的吸引域。具体算法如下：

算法2：

以地面移动机器人与水下航行器为例。假设地面机器人规定10m/s的向前移动速度，通过调节转向让机器人进行安全避障，如图1-4所示。图5-6为水下机器人，其可以进行速度调节，并从开始点到目标点进行避障运动。如图所示：

如图1-6所示，图1粗实线显示PRM算法在存在障碍物情况下规划出的不同轨迹，星型为PRM路径节点。虚线为非线性规划后得到满足动力学特性的开环轨迹，黑色为障碍物。图2计算图1开环标称轨迹的吸引域(黑色包络区域)作为高斯估计的离散数据库。

图3显示了当无法进行测量的情况下预先估计的轨迹因为无法保证实际吸引域的存在而无法完成路径，因此图3为一条不可行路径。但是传统的吸引域算法得到吸引域(黑色区域)依然可以通往目标，而实际机器人则无法完成这样的路径(白色内环为计算得到的鲁棒吸引域，随着机器人的前进起逐渐衰减到零)。如果在障碍物附近可以进行测量，则真实的白色内环吸引域可以持续延伸至目标点，从而完成安全路径。

图5和图6显示了水下航行器的可行路径，半圆为可获得测量值的范围，从图中可以看出当路径经过可测量的范围吸引域范围明显增加，可持续至目标点，从而保证路径规划的安全可行性。

从仿真结果可以看出本发明所提出算法的有效性。本算法可以形成全局鲁棒的吸引域路径，从而满足安全快速的轨迹规划要求。

以上内容仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明权利要求书的保护范围之内。