一种飞行器系统的配平方法和装置与流程

本发明涉及飞行器技术领域，更具体的说，是涉及一种飞行器系统的配平方法和装置。

背景技术：

在飞行器技术领域中，飞行器控制系统的设计好坏直接影响着飞行器在实际飞行中的操作。

以固定翼飞机为例，飞行器控制系统的设计中需要将整个飞行剖面展开，分解成多个工作点，每个工作点包括各自的高度、马赫数等参数，然后分别对所有工作点进行配平，得到多个配平结果，利用多个配平结果对非线性飞机方程进行线性化得到纵向小扰动方程。最后根据纵向小扰动方程实现对飞行器控制系统的设计。

其中，利用配平方法得到配平结果是最为关键的部分。现有的配平方法中，较为常用的是基于数值迭代的配平方法，如利用牛顿迭代、非线性规划和智能算法等的配平方法。但是，由于固定翼飞机的纵向小扰动方程具有强非线性，而牛顿迭代等迭代过程较为简单，会导致求解失败，无法得到配平结果。

为了解决求解失败的问题，现有技术提出了采用基于序贯二次规划、神经网络等算法的配平方法，使用这些配平方法不会求解失败，且得到的配平结果精确度较高，但是，这些算法都需要使用动力学运动学方程，而动力学运动学方程的计算过程都比较复杂，计算量大。

技术实现要素：

有鉴于此，本发明提供了一种飞行器系统的配平方法和装置，在得到配平结果的过程中，计算量小且可以保证配平结果的精确度。

本发明提供的一种飞行器系统的配平方法，包括：

获取与指定工作点相匹配的工作点参数，所述工作点参数包括高度、马赫数、质量和转动惯量；

根据所述高度、所述马赫数以及预设配平参数得到气动力数据；

根据所述质量、所述转动惯量以及所述气动力数据得到变化率参数；

根据所述变化率参数确定所述飞行器是否处于稳定状态；

若处于稳定状态，则将所述预设配平参数作为配平结果；

若不处于稳定状态，利用所述变化率参数更新所述预设配平参数并返回所述根据所述高度、所述马赫数以及预设配平参数得到气动力数据的步骤。

优选的，所述根据所述高度、所述马赫数以及预设配平参数得到气动力数据包括：

使用预设算法根据所述高度、所述马赫数以及所述预设配平参数得到气动参数差值变量；

使用所述气动参数差值变量查找预设气动参数差值表，得到与所述气动参数差值变量相匹配的气动导数；

将所述气动导数通过预设气动力计算公式计算得到气动力数据。

优选的，所述气动力数据至少包括纵向合外力、前向合外力以及力矩，则根据所述质量、所述转动惯量以及所述气动力数据得到变化率参数包括：

根据所述纵向合外力以及所述质量计算得到纵向速度变化率；

根据所述力矩以及所述转动惯量计算得到角速度变化率；

根据所述前向合外力以及所述质量计算得到前向速度变化率；

将所述纵向速度变化率、所述角速度变化率以及所述前向速度变化率作为变化率参数。

优选的，所述根据所述变化率参数确定所述飞行器是否处于稳定状态包括：

判断所述纵向速度变化率是否小于预设纵向速度变化率，得到第一判断结果；

判断所述角速度变化率是否小于预设角速度变化率，得到第二判断结果；

判断所述前向速度变化率是否小于预设前向速度变化率，得到第三判断结果；

若所述第一判断结果、所述第二判断结果以及所述第三判断结果均为是，则确定所述飞行器处于稳定状态；否则，确定所述飞行器不处于稳定状态。

优选的，所述利用所述变化率参数更新所述预设配平参数包括：

根据所述纵向速度变化率与预设纵向速度变化率，得到纵向速度变化率参数；

根据所述角速度变化率与预设角速度变化率，得到角速度变化率参数；

根据所述纵向速度变化率参数以及所述角速度变化率参数对所述预设配平参数进行更新。

本发明另一方面提供了一种飞行器系统的配平装置，包括：

工作点参数获取单元，用于获取与指定工作点相匹配的工作点参数，所述工作点参数包括高度、马赫数、质量和转动惯量；

气动力数据计算单元，用于根据所述高度、所述马赫数以及预设配平参数得到气动力数据；

变化率参数计算单元，用于根据所述质量、所述转动惯量以及所述气动力数据得到变化率参数；

判断单元，用于根据所述变化率参数确定所述飞行器是否处于稳定状态；

第一执行单元，用于若所述飞行器处于稳定状态，则将所述预设配平参数作为配平结果；

第二执行单元，用于若所述飞行器不处于稳定状态，利用所述变化率参数更新所述预设配平参数并返回所述气动力数据计算单元。

优选的，所述气动力数据计算单元包括：

第一计算模块，用于使用预设算法根据所述高度、所述马赫数以及所述预设配平参数得到气动参数差值变量；

第二计算模块，用于使用所述气动参数差值变量查找预设气动参数差值表，得到与所述气动参数差值变量相匹配的气动导数；

第三计算模块，用于将所述气动导数通过预设气动力计算公式计算得到气动力数据。

优选的，所述气动力数据至少包括纵向合外力、前向合外力以及力矩，则所述变化率参数计算单元包括：

纵向速度变化率计算模块，用于根据所述纵向合外力以及所述质量计算得到纵向速度变化率；

角速度变化率计算模块，用于根据所述力矩以及所述转动惯量计算得到角速度变化率；

前向速度变化率计算模块，用于根据所述前向合外力以及所述质量计算得到前向速度变化率；

变化率数参数确定模块，用于将所述纵向速度变化率、所述角速度变化率以及所述前向速度变化率作为变化率数参数。

优选的，所述判断单元包括：

第一判断模块，用于判断所述纵向速度变化率是否小于预设纵向速度变化率，得到第一判断结果；

第二判断模块，用于判断所述角速度变化率是否小于预设角速度变化率，得到第二判断结果；

第三判断模块，用于判断所述前向速度变化率是否小于预设前向速度变化率，得到第三判断结果；

确定模块，用于若所述第一判断结果、所述第二判断结果以及所述第三判断结果均为是，则确定所述飞行器处于稳定状态；否则，确定所述飞行器不处于稳定状态。

优选的，所述第二执行单元包括：

纵向速度变化率参数计算模块，用于根据所述纵向速度变化率与预设纵向速度变化率，得到纵向速度变化率参数；

角速度变化率参数计算模块，用于根据所述角速度变化率与预设角速度变化率，得到角速度变化率参数；

更新模块，用于根据所述纵向速度变化率参数以及所述角速度变化率参数对所述预设配平参数进行更新。

经由上述的技术方案可知，与现有技术相比，本发明公开了一种飞行器系统的配平方法和装置，所述配平方法首先获取与指定工作点相匹配的工作点参数，所述工作点参数包括高度、马赫数、质量和转动惯量；然后根据所述高度、所述马赫数以及预设配平参数得到气动力数据；根据所述质量、所述转动惯量以及所述气动力数据得到变化率数参数；最后根据所述变化率参数确定所述飞行器是否处于稳定状态；若处于稳定状态，则将所述预设配平参数作为配平结果；若不处于稳定状态，利用所述变化率参数更新所述预设配平参数并返回所述根据所述高度、所述马赫数以及预设配平参数得到气动力数据的步骤。由于在配平方法中，并不会使用动力学运动学方程，因此，计算难度小、过程简单，并且在飞行器不处于稳定状态时，会自动更新预设配平参数，并经过重新计算得到配平结果，从而保证了配平结果的精度。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1为本发明提供的一种飞行器系统的配平方法的流程示意图；

图2为本发明提供的一种飞行器系统的配平方法的逻辑计算框图；

图3为本发明实施例中得到气动力数据的流程示意图；

图4为本发明实施例中得到变化率参数的流程示意图；

图5A为本发明实施例中采用蒙特卡洛随机法进行仿真得到配平推力计算结果的曲线图；

图5B为本发明实施例中采用蒙特卡洛随机法进行仿真得到配平攻角计算结果的曲线图；

图5C为本发明实施例中采用蒙特卡洛随机法进行仿真得到配平升降舵偏角计算结果的曲线图；

图6为本发明提供的一种飞行器系统的配平装置的结构示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明技术方案的核心思路是将控制思想与迭代执行相结合，基于控制的思想建立配平参数更新逻辑，采用迭代方式进行求解，计算过程不涉及动力学运动学环节，使得算法不论在实现还是运算上都具有快速性；通过自适应调整迭代参数，使得算法适应性、计算效率更好。

下面对本发明的技术方案进行详细介绍。

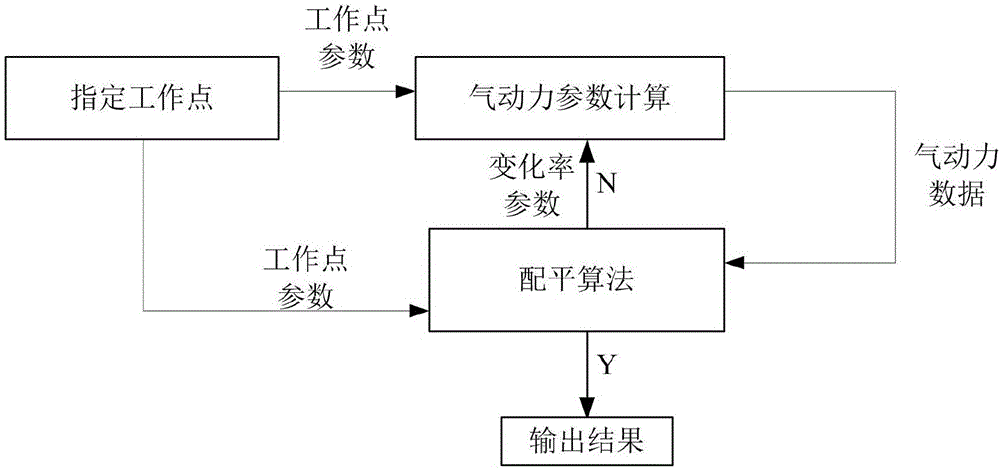
参见图1、图2，图1为本发明提供的一种飞行器系统的配平方法的流程示意图，图2为本发明提供的一种飞行器系统的配平方法的逻辑计算框图。

本发明提供了一种飞行器系统的配平方法，包括：

S101、获取与指定工作点相匹配的工作点参数，所述工作点参数包括高度、马赫数、质量和转动惯量；

本发明实施例，可以使用在仿真系统中，也可以直接应用到飞行器系统中，本发明优选应用在飞行器控制系统俯仰通道中，飞行器优选采用固定翼飞机。

本发明实施例中，首先获取与指定工作点相匹配的工作点参数。其中，指定工作点是根据用户的需要预先进行设置的或选择的。

工作点参数具体包括高度、马赫数、质量和转动惯量。这些参数通过设计要求确定。

S102、根据所述高度、所述马赫数以及预设配平参数得到气动力数据；

S103、根据所述质量、所述转动惯量以及所述气动力数据得到变化率参数；

在获取到工作点参数后，根据工作点参数中的高度和马赫数以及预设配平参数，得到气动力数据。气动力数据通常包括根据飞行器所受的气动力和气动力矩计算出的合力和力矩。

需要说明的是，步骤S102中得到气动力数据的过程中所计算出的数据是变化量数据。具体的计算过程在后面详细介绍。

其中，预设配平参数是预估或猜测值。具体可以包括：配平攻角theta、配平推力p和配平升降舵偏角stb的初始配平猜测值。

具体的，配平攻角和配平升降舵偏角的初始配平猜测值设为0，配平推力的初始配平猜测值根据不同飞机推力性能选取一个中间值(如某一个飞机的推力范围是[Fmin,Fmax]，则可选初始配平猜测值为1/2*(Fmin+Fmax))。

之后根据所述质量、所述转动惯量以及所述气动力数据得到变化率参数。得到变化率参数的具体计算过程在后面进行详细介绍。

其中，变化率数参数可以包括：纵向速度变化率、角速度变化率以及前向速度变化率。

需要说明的是，此步骤中同时还计算出当前工作点的前向速度以供后续更新使用，前向速度Vt使用Vt＝340*Ma计算得到，其中340为声速值，Ma为马赫数。

S104、根据所述变化率参数确定所述飞行器是否处于稳定状态；

变化率参数用于表征飞行器的高度、速度以及姿态的变化。当飞行器的纵向速度变化率、角速度变化率以及前向速度变化率均满足飞行器稳定时的判断条件时，证明飞行器的高度稳定、速度稳定并且姿态稳定，意味着配平成功，此时飞行器处于稳定状态。

因此，在得到变化率参数后，根据所述变化率参数确定所述飞行器是否处于稳定状态。具体的确定过程在后面进行详细介绍。

S105、若处于稳定状态，则将所述预设配平参数作为配平结果；

S106、若不处于稳定状态，利用所述变化率参数更新所述预设配平参数并返回步骤S102。

如果飞行器处于稳定状态，则意味着本次配平成功，将预设配平参数作为配平结果。

在实际使用中，预设配平参数可以包括多个，例如攻角、推力和升降舵偏角，以及俯仰角和纵向速度。将预设配平参数作为配平结果可以是将攻角、推力和升降舵偏角作为配平结果。当然，也可以输出全部数据作为配平结果。

如果不处于稳定状态，则意味着本次配平不成功，则利用所述变化率参数更新所述预设配平参数。返回到步骤S102中继续运算，循环迭代，直到配平成功。

经由上述的技术方案可知，由于本发明公开的一种飞行器系统的配平方法中，仅需要工作点参数和预设配平参数就可以得到配平结果，需要的运算条件少，并不需要动力学运动学方程，并且自适应更新预设配平参数的方式使得最后的配平结果也比较准确，在运算简单的前提下保证了配平结果的准确度。

上述方案中，介绍了得到气动力数据的过程，下面详细介绍步骤S102。

参见图3所示，图3为本发明实施例中得到气动力数据的流程示意图。

所述根据所述高度、所述马赫数以及预设配平参数得到气动力数据包括：

S301、使用预设算法根据所述高度、所述马赫数以及所述预设配平参数得到气动参数差值变量；

本发明实施例中，根据高度和马赫数结合预设配平参数得到气动参数差值变量。

实际使用中，使用高度、马赫数和初始配平猜测值利用成熟的算法进行计算，计算必要的气动参数差值变量；差值变量的类型依飞行器对象而定，一般包括动压、舵偏角、攻角，当然还可以计算出其它的差值变量。

S302、使用所述气动参数差值变量查找预设气动参数差值表，得到与所述气动参数差值变量相匹配的气动导数；

得到气动参数差值变量后，气动参数差值变量进入气动参数差值表计算得到气动导数。

其中，气动参数差值表是一个查询表，包含有预先建立的气动参数差值变量和气动导数值的对应关系，输入气动参数差值变量的不同数，将输出与之对应的气动导数值。

S303、将所述气动导数通过预设气动力计算公式计算得到气动力数据。

最后，气动导数经过气动力计算公式得到飞行器所受的气动力和气动力矩，并计算纵向合外力、前向合外力和力矩。

上述过程可以理解为气动力数据的计算过程。

得到气动力数据之后，需要利用气动力数据计算变化率参数，下面详细对此过程进行介绍。

参见图4，图4公开了本发明实施例中得到变化率参数的流程示意图。

所述气动力数据至少包括纵向合外力、前向合外力以及力矩，则根据所述质量、所述转动惯量以及所述气动力数据得到变化率参数包括：

S401、根据所述纵向合外力以及所述质量计算得到纵向速度变化率；

S402、根据所述力矩以及所述转动惯量计算得到角速度变化率；

S403、根据所述前向合外力以及所述质量计算得到前向速度变化率；

本发明实施例中，纵向速度变化率使用公式纵向速度变化率Vy_dot＝Fz/Mass进行计算，其中Fz为纵向合外力，Mass为质量。

角速度变化率使用公式角速度变化率q_dot＝My/Iy进行计算，其中My为力矩、Iy为转动惯量。

前向速度变化率使用公式前向速度变化率Vt_dot＝Fx/Mass进行计算，其中Fx为前向合外力，Mass为质量。

S404、将所述纵向速度变化率、所述角速度变化率以及所述前向速度变化率作为变化率参数。

前述介绍了根据所述变化率参数确定所述飞行器是否处于稳定状态，下面具体对此过程进行介绍。

根据所述变化率参数确定所述飞行器是否处于稳定状态包括：

判断所述纵向速度变化率是否小于预设纵向速度变化率，得到第一判断结果；

判断所述角速度变化率是否小于预设角速度变化率，得到第二判断结果；

判断所述前向速度变化率是否小于预设前向速度变化率，得到第三判断结果；

若所述第一判断结果、所述第二判断结果以及所述第三判断结果均为是，则确定所述飞行器处于稳定状态；否则，确定所述飞行器不处于稳定状态。

本发明实施例中，在得到了所述纵向速度变化率、所述角速度变化率以及所述前向速度变化率之后，判断所述纵向速度变化率是否小于预设纵向速度变化率，得到第一判断结果；如果是，则第一判断结果为是。

判断所述角速度变化率是否小于预设角速度变化率，得到第二判断结果；如果是，则第二判断结果为是。

判断所述前向速度变化率是否小于预设前向速度变化率，得到第三判断结果。如果是，则第三判断结果为是。

如果三个判断结果都为是，则确定所述飞行器处于稳定状态；否则，确定所述飞行器不处于稳定状态。通过判断上述三个变化率是否均小于各自对应的预设值，可以确定对飞行器的配平是否成功，原因在于：配平成功的标志就是飞机的高度、速度以及姿态的稳定。其中，高度稳定表现为纵向速度变化率小于某一预设值；速度稳定表现为前向速度变化率小于某一预设值；姿态稳定表现为角速度变化率小于某一预设值。因此，当这三个变化率均小于各自对应的预设值时，则确定飞行器处于稳定状态，即表明配平成功。

若飞行器不处于稳定状态，则需要对预设配平参数进行更新。下面对利用所述变化率数参数更新所述预设配平参数进行介绍。

所述利用所述变化率数参数更新所述预设配平参数包括：

与预设纵向速度变化率，得到纵向速度变化率参数；

本发明实施例中，如果飞行器不处于稳定状态，即配平不成功，利用自适应的方式进行自动调整。

纵向速度变化率参数为K_Vy_dot，其取值根据收敛情况的需求由设计人员给出，如：

如果Vy_dot<Tol_Vy_dot，则K_Vy_dot＝0.01Vy_dot；其中，Tol_Vy_dot为预设纵向速度变化率；

否则K_Vy_dot＝Vy_dot。

这是因为，如果Vy_dot<Tol_Vy_dot，则表示Vy的偏差已经比较小了，为了可以满足Vy_dot<Tol_Vy_dot，应选取较小的K_Vy_dot值，K_Vy_dot＝0.01Vy_dot。否则，说明Vy值偏差还较大，选择较大的K_Vy_dot使得算法较快收敛，K_Vy_dot＝Vy_dot。

K_Vy_dot选择Vy_dot是为了提高收敛速度，选择0.01Vy_dot是为了增加收敛精度。如果选择过小如0.0001，会影响Tol_Vy_dot的可达到性，当然，如果选的过大Tol_Vy_dot可能永远达不到。

根据所述角速度变化率与预设角速度变化率，得到角速度变化率参数；

角速度变化率参数K_q_dot，其取值根据收敛情况的需求由设计人员给出，如：

如果q_dot<Tol_q_dot，则K_q_dot＝0.1q_dot；

否则K_q_dot＝q_dot。

使用所述纵向速度变化率参数以及所述角速度变化率参数对所述预设配平参数进行更新。

更新预设配平参数，前述介绍了预设配平参数可以包括纵向速度、俯仰角、升降舵偏角、推力、攻角。在得到了所述纵向速度变化率参数以及所述角速度变化率参数，并结合之前计算出的前向速度Vt对预设配平参数进行更新。

具体的：

纵向速度Vy更新：Vy＝Vy1+sign(K_Vy_dot)，其中，Vy表示更新后的纵向速度，Vy1表示更新前预设配平参数中的纵向速度，其中sign为符号函数；

俯仰角theta更新：theta＝alpha，将攻角alpha作为更新后的俯仰角theta；

升降舵偏角stb更新：stb＝stb1+My*K_q_dot，其中，stb为更新后的升降舵偏角，stb1表示更新前预设配平参数中的升降舵偏角，My为力矩，并限制其值在容许的最小偏角stb_l和最大偏角之间stb_u；

推力P更新：P＝-Fax+sin(theta)*Mass*g，其中Fax为前向加速度，Mass为质量，g为重力加速度；sin为数学三角符号，theta为更新后的俯仰角；限制P值在容许的最小偏角P_l和最大偏角P_u之间；

攻角alpha更新：alpha＝theta-asin(Vy/sqrt(Vt^2-Vy^2))，其中，式中的theta指更新后的俯仰角，Vy表示更新后的纵向速度，asin()为反余弦函数，sqrt()为开根号函数。

根据上述方式，完成了对预设配平参数的更新。

根据上述配平方法，进行配平仿真，为了验证算法的性能，采用蒙特卡洛随机法进行仿真，随机设置10次初始配平猜测值，仿真结果如图5所示。其中图5A中的配平推力对应本发明实施例中预设配平参数中的推力，图5B中的配平攻角对应本发明实施例中预设配平参数中的攻角，图5C中的配平升降舵偏角对应本发明实施例中预设配平参数中的升降舵偏角。

由图5A、图5B、图5C可见，针对所有仿真，算法均在约1300次迭代之前配平成功。且由于算法实现简单，每组仿真计算时间仅约1秒。

本发明针对俯仰通道使用的自适应配平方法，可以很好的解决对飞行器非线性系统俯仰通道的配平问题，该方法和思路也可以用于水平通道的配平。

因此，本发明实施例不需要针对不同的飞机对象的所有工作点分别建立合适的控制器，通用性较强。

本发明另一方面提供了一种飞行器系统的配平装置。

参见图6，本发明提供的一种飞行器系统的配平装置包括：

工作点参数获取单元601，用于获取与指定工作点相匹配的工作点参数，所述工作点参数包括高度、马赫数、质量和转动惯量；

气动力数据计算单元602，用于根据所述高度、所述马赫数以及预设配平参数得到气动力数据；

变化率参数计算单元603，用于根据所述质量、所述转动惯量以及所述气动力数据得到变化率数参数；

判断单元604，用于根据所述变化率参数确定所述飞行器是否处于稳定状态；

第一执行单元605，用于若所述飞行器处于稳定状态，则将所述预设配平参数作为配平结果；

第二执行单元606，用于若所述飞行器不处于稳定状态，利用所述变化率参数更新所述预设配平参数并返回所述气动力数据计算单元。

优选的，所述气动力数据计算单元602包括：

第一计算模块，用于使用预设算法根据所述高度、所述马赫数以及所述预设配平参数得到气动参数差值变量；

第二计算模块，用于使用所述气动参数差值变量查找预设气动参数差值表，得到与所述气动参数差值变量相匹配的气动导数；

第三计算模块，用于将所述气动导数通过预设气动力计算公式计算得到气动力数据。

优选的，所述气动力数据至少包括纵向合外力、前向合外力以及力矩，则所述变化率参数计算单元603包括：

纵向速度变化率计算模块，用于根据所述纵向合外力以及所述质量计算得到纵向速度变化率；

角速度变化率计算模块，用于根据所述力矩以及所述转动惯量计算得到角速度变化率；

前向速度变化率计算模块，用于根据所述前向合外力以及所述质量计算得到前向速度变化率；

变化率数参数确定模块，用于将所述纵向速度变化率、所述角速度变化率以及所述前向速度变化率作为变化率数参数。

优选的，所述判断单元604包括：

第一判断模块，用于判断所述纵向速度变化率是否小于预设纵向速度变化率，得到第一判断结果；

第二判断模块，用于判断所述角速度变化率是否小于预设角速度变化率，得到第二判断结果；

第三判断模块，用于判断所述前向速度变化率是否小于预设前向速度变化率，得到第三判断结果；

确定模块，用于若所述第一判断结果、所述第二判断结果以及所述第三判断结果均为是，则确定所述飞行器处于稳定状态；否则，则确定所述飞行器不处于稳定状态。

优选的，

所述第二执行单元606具体包括：

纵向速度变化率参数计算模块，用于根据所述纵向速度变化率与预设纵向速度变化率，得到纵向速度变化率参数；

角速度变化率参数计算模块，用于根据所述角速度变化率与预设角速度变化率，得到角速度变化率参数；

更新模块，用于使用所述纵向速度变化率参数以及所述角速度变化率参数对所述预设配平参数进行更新。

经由上述的技术方案可知，与现有技术相比，本发明公开了一种飞行器系统的配平装置，所述配平装置首先获取与指定工作点相匹配的工作点参数，所述工作点参数包括高度、马赫数、质量和转动惯量；然后根据所述高度、所述马赫数以及预设配平参数得到气动力数据；根据所述质量、所述转动惯量以及所述气动力数据得到变化率参数；最后根据所述变化率参数确定所述飞行器是否处于稳定状态；若处于稳定状态，则将所述预设配平参数作为配平结果；若不处于稳定状态，利用所述变化率参数更新所述预设配平参数并返回所述根据所述高度、所述马赫数以及预设配平参数得到气动力数据的步骤。由于在配平装置并不会使用动力学运动学方程，因此，计算难度小、过程简单，而且在飞行器不处于稳定状态时，自动更新预设配平参数，经过重新计算得到配平结果，保证了配平结果的精度。

需要说明的是，本说明书中的各个实施例均采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似的部分互相参见即可。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的这些实施例，而是要符合与本文所公开的原理和新颖特点相一致的最宽的范围。