一种基于免疫粒子群算法的温度控制方法与流程
本发明涉及过程控制技术领域,特别是涉及一种基于免疫粒子群算法的温度控制方法。
背景技术:
以某化工厂聚乙烯生产为背景,对聚合温度的控制进行研究。大多数的化工厂对温度的控制,通常使用传统的PID控制器。但是由于传统的PID在工业中不能满足对高扰动的要求,所以单纯使用会有不足之处。
PID控制器具有适应性强、操作简便、鲁棒性好等特点,因此在实际的生产控制过程中会优先考虑使用PID控制器来调节温度的变化。但是大多数的PID参数优化主要是在经验指导下进行的,因此不能很好适用于生产中的各种情况。其次,由于传统的PID存在超调量大,积分容易饱和等缺点。所以单纯的传统PID是不能满足工业生产中对于高扰动的要求。如今,将自适应控制、最优控制、预测控制、鲁棒控制和智能控制策略引入传统PID控制,逐步发展成为一种新型PID控制。
PSO算法是用来对空间进行全局最优搜索的一种算法。它的优点是参数较少,收敛速度相对较快,具有很强的全局优化能力。但是PSO算法的缺点是容易在优化的后期陷入收敛速度慢并且容易出现局部最优。但是免疫算法具有免疫和遗传等优点,所以将免疫算法和PSO算法相结合,就可以克服PSO算法的缺点。因此可以考虑将PSO算法和免疫算法相结合用于对PID控制器的调节。
免疫算法是鉴于生物自身的免疫反应而发展出来的一种算法。免疫算法可以通过抗体的多样性以及自我的调节来保证种群的多样性,这样就可以解决在后期的优化出现早熟的问题,确保了群体可以向最优解的方向快速收敛。
将免疫算法和PSO算法相结合,就可以将抗原视为待求解的问题,抗体视为问题的解,并且抗体也是粒子群中的粒子。用适应度函数去衡量抗原与抗体的紧密程度,抗体之间的浓度反映了粒子群的的多样性。免疫粒子群算法既可以通过免疫算法中的免疫记忆以及自我调节保持粒子群的多样性,也可以通过PSO算法让抗体可以朝一个方向进行进化,从而在较少的代数内向最优解进行收敛。
技术实现要素:
本发明所要解决的技术问题是提供一种基于免疫粒子群算法的温度控制方法,不仅满足了对温度的控制要求,而且还大大降低了经济成本。
本发明解决其技术问题所采用的技术方案是:提供一种基于免疫粒子群算法的温度控制方法,包括以下步骤:
(1)确定需要控制的目标温度值;
(2)对采用基于免疫粒子群算法的各种参数进行计算,得到最优的值;
(3)通过仿真的方式比较采用基于免疫粒子群算法前后的差异;
(4)确定在实际生产中温度的控制形式,并实现控制。
所述步骤(2)具体为:首先确定学习因子、惯性因子的范围、种群大小、待求问题的维数、最大迭代次数和搜索范围;随机产生初始化种群N,将粒子的速度设为0,通过计算适应值得到个体极值和全局极值;对每一个粒子的速度和位置进行计算;比较每一个粒子更新前后的适应度值;如果更新后的粒子适应值增加了,那么就保存该粒子更新后的位置和速度;将全局最优极值作为系统的“疫苗”;使用“疫苗”对每个粒子进行接种;并对接种后的粒子进行适应值的计算,来判断粒子的好坏;如果更新后的适应值大于更新前的适应值,那么就保存该粒子,否则舍弃;此时会形成一个新的粒子群,计算新粒子群的个体极值和全局极值;如果运算的迭代次数大于最大的迭代次数,那么输出结果,否则重复上述步骤。
所述对每一个粒子的速度和位置进行计算时采用的公式为vk+1=wvk+c1r1(pbestk-xk)+c2r2(gbestk-xk)和xk+1=xk+vk+1,其中,vk为粒子更新前的速度值,vk+1为粒子更新后的速度值,xk为粒子更新前的位置值,xk+1为粒子更新后的位置值,c1、c2为常数,r1、r2为分布于[0,1]区间内的随机数,pbestk为个体极值、gbestk为全局极值,w为惯性因子。
所述步骤(3)采用MATLAB进行仿真。
所述步骤(4)中通过西门子的WINCC软件所绘制出来的动态监控图监控反应釜内温度的变化。
有益效果
由于采用了上述的技术方案,本发明与现有技术相比,具有以下的优点和积极效果:本发明通过对PID控制器参数的整定来控制聚乙烯生产过程中的阀门开关的程度,从而达到对温度的控制。本发明可以使温度波动在50±0.2℃,充分的满足了聚乙烯生产中对温度的控制要求。
附图说明
图1是本发明的基于免疫粒子群算法流程图;
图2是本发明的系统整定之前的MATLAB仿真图;
图3是本发明的系统整定之后的MATLAB仿真图;
图4是本发明的免疫粒子群算法与PSO算法比较图。
具体实施方式
下面结合具体实施例,进一步阐述本发明。应理解,这些实施例仅用于说明本发明而不用于限制本发明的范围。此外应理解,在阅读了本发明讲授的内容之后,本领域技术人员可以对本发明作各种改动或修改,这些等价形式同样落于本申请所附权利要求书所限定的范围。
本发明的实施方式涉及一种基于免疫粒子群算法的温度控制方法,包括以下步骤:确定需要控制的目标温度值;对采用基于免疫粒子群算法的各种参数进行计算,得到最优的值;通过仿真的方式比较采用基于免疫粒子群算法前后的差异;确定在实际生产中温度的控制形式,并实现控制。其中,在进行仿真时可以采用MATLAB进行仿真,在进行控制时可以通过西门子的WINCC软件所绘制出来的动态监控图监控反应釜内温度的变化。
采用基于免疫粒子群算法的各种参数进行计算,得到最优的值的具体步骤如下,如图1所示:
步骤1:首先确定学习因子,惯性因子w的范围,种群大小,待求问题的维数,最大迭代次数以及搜索的范围。
步骤2:随机产生初始化种群N,将粒子的速度设为0,防止因为速度太大而超出了搜索范围。通过计算适应值得到个体极值和全局极值。
步骤3:用公式vk+1=wvk+c1r1(pbestk-xk)+c2r2(gbestk-xk)和xk+1=xk+vk+1对每一个粒子的速度和位置进行计算。其中,vk为粒子更新前的速度值,vk+1为粒子更新后的速度值,xk为粒子更新前的位置值,xk+1为粒子更新后的位置值,c1、c2为常数,r1、r2为分布于[0,1]区间内的随机数,pbestk为个体极值、gbestk为全局极值,w为惯性因子。
步骤4:比较每一个粒子更新前后的适应度值。如果更新后的粒子适应值增加了,那么就保存该粒子更新后的位置和速度。
步骤5:将全局最优极值gbest作为系统的“疫苗”。
步骤6:使用“疫苗”对每个粒子进行接种。并对接种后的粒子进行适应值的计算,来判断粒子的好坏。如果更新后的适应值大于更新前的适应值,那么就保存该粒子,否则舍弃。此时会形成一个新的粒子群。
步骤7:用公式vk+1=wvk+c1r1(pbestk-xk)+c2r2(gbestk-xk)和xk+1=xk+vk+1计算新粒子群的个体极值pbest和全局最优极值gbest。
步骤8:如果运算的迭代次数大于最大的迭代次数,那么输出结果,否则回到步骤2。
经过以上步骤,就可以得出该算法适合的参数。将其用MATLAB仿真。
如图2所示,在对PID控制器进行整定之前的函数图像。该图像显示了在500s之后,函数的振动幅度开始减小并且在1000s之后开始趋于稳定。由此可以看出,该系统还具有很大的提升空间。因此使用基于免疫粒子群算法可以大大提升该系统的动态性能。
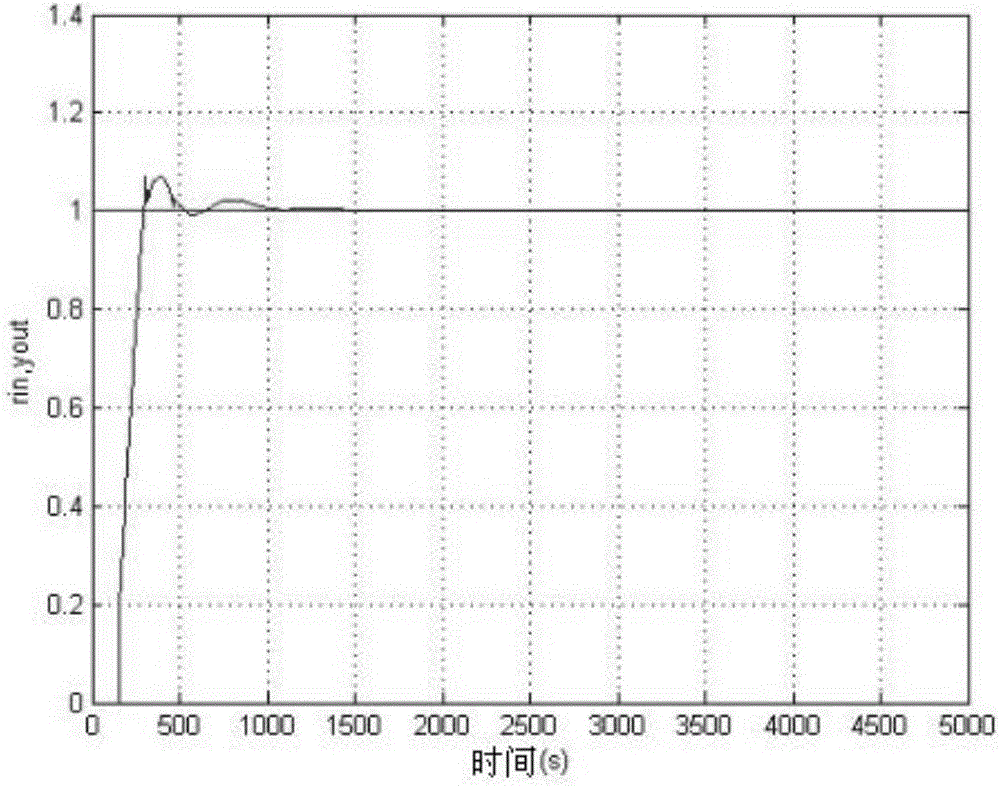
如图3所示,通过加入基于免疫粒子群算法之后,该图像显示了系统良好的动态性能。在经历了大约250s之后,函数的振动幅度开始减小并且在大约700之后开始趋于稳定,并且整定之后的系统时域性能指标要优于整定之前的系统时域性能指标。
如图4所示,将基于免疫粒子群算法和单纯的粒子群算法进行比较,会发现免疫粒子群的超调量为0.0845,调节时间为700s。粒子群算法的超调量为0.4021,调节时间为1400s。所以免疫粒子群算法整定的PID控制器的控制效果要优于单纯的粒子群算法。
不难发现,采用本发明通过对PID控制器参数的整定来控制聚乙烯生产过程中的阀门开关的程度,从而达到对温度的控制。本发明可以使温度波动在50±0.2℃,充分的满足了聚乙烯生产中对温度的控制要求。
- 还没有人留言评论。精彩留言会获得点赞!