一种基于β参数的多峰值最大电功率跟踪控制方法与流程

本发明涉及光伏系统，特别涉及一种基于β参数的多峰值最大电功率跟踪控制方法。

背景技术：

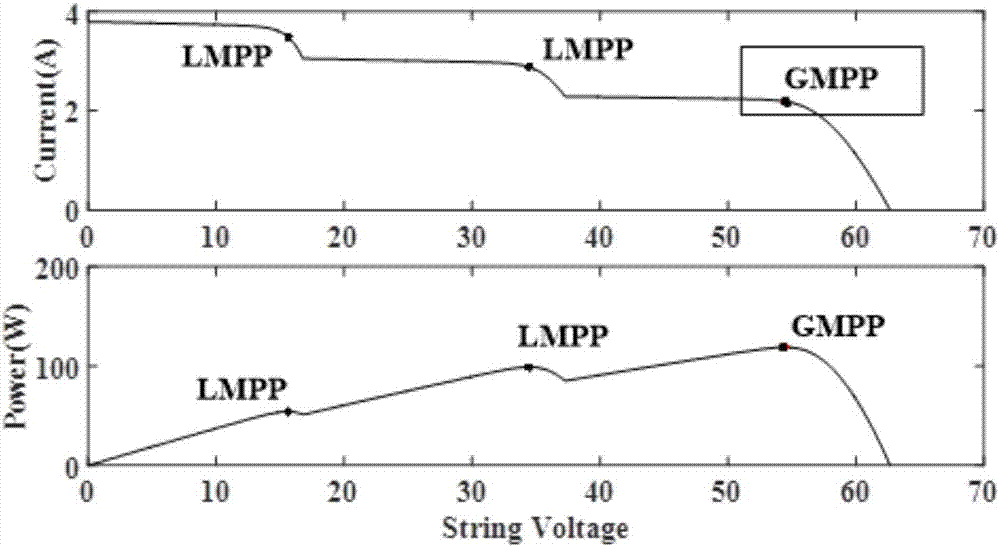
当光伏组串发生局部遮挡时，如图1所示，其p-v曲线上会出现多个局部最大功率点(localmaximumpowerpoint，lmpp)和一个全局最大功率点(globalmaximumpowerpoint，gmpp)，如图2所示。此时，传统的mppt算法如，扰动观察法(perturb&observe，p&o)、电导增量法(incrementalconductance，inc)、beta法等，可能将无法输出在其最大功率，从而造成发电效率下降。

为了能够解决这问题，很多gmppt算法被提出。根据其算法类型，可大致分为以下三种：

(1)人工智能(artificialintelligent，ai)算法，如模糊逻辑(fuzzylogiccontrol，flc)，粒子群优(particleswarmoptimization，pso)，模拟退火(simulatedannealing，sa)等。其优点在于追踪精度高，适应性强。但其缺点主要在于计算复杂、实现困难，且需要人工设定大量参数以确保其能稳定工作。

(2)阶段性搜索方法(segmentalsearch)。此类算法一般基于一些数学理论，如斐波纳契线性搜索(fibonaccilinesearch)、利普希茨连续(lipschitzcontinuity)等。此类算法与ai算法相比较为简单、易于实现，且适应性较强。但是，其准确性较低，有可能找不到gmpp。

(3)两步法(two-stagemethod)。此类算法一般分为两步：首先，算法先找到所有lmpp，并从中确定gmpp；然后，传统的mppt算法，如p&o、inc等，用来精确追踪gmpp并将其维持以输出最大功率。相对于前两种方法，此类算法更为灵活。其算法实现难易度、追踪精确度以及算法适应度主要取决于其算法第一步，即如何确定gmpp的大致位置。目前，此类算法大多数基于0.8voc的算法模型，其代表作为h.patel所提出的算法。

虽然h.patel算法优点在于简单明了。但是，其缺点主要在于1)可能存在误判的现象；2)追踪速度慢，效率低。

基于以上论述，本文提出一种基于β参数的多峰值最大电功率跟踪控制方法。此算法不仅追踪精确度高，而且简单明了易于实现，同时还能确保追踪速度快，效率高。

技术实现要素：

本发明目的是：提供一种基于β参数的多峰值最大电功率跟踪控制方法，追踪精确度高，简单明了易于实现，同时还能确保追踪速度快，效率高。

本发明的技术方案是：

1.一种基于β参数的多峰值最大电功率跟踪控制方法，包括：

s1、首先定义光伏组串的等效主导电压vdomi，为

vdomi＝vstring-(n-1)×vs+(m-n)×vd(1)；

其中vstring为整个光伏组串的输出电压，m为光伏组串的光伏组件数量，n为

其中，voc为光伏组件的开路电压，α为常量；

公式(1)中，vd为光伏组件的旁路二极管压降，vs为线性直流电压源，其近似为

其中vmpp,stc、impp,stc为光伏组件在标准测试环境下位于mpp点的电压、电流值；voc,stc为光伏组件在标准测试环境下开路电压；

s2、根据公式(1)-(3)，将整个光伏组串的i-v曲线进行划分，划分出带有峰值的曲线部分；

s3、定义变量βdomi，为

其中c＝q/(nsakt)，是光伏特性参数；根据公式(4)，可将步骤s2中划分的每部分进一步进行划分，使所有的峰值，包括lmpp和gmpp，均在βmax和βmin范围内。

s4、再采用传统的beta法，分别步骤s3划分的区间进行追踪，求出整个光伏组串的gmpp。

优选的，所述常量α，其值设为0.8～0.95之间。

本发明的优点是：

本发明提出的一种基于β参数的多峰值最大电功率跟踪控制方法，不仅追踪精确度高，而且简单明了易于实现，同时还能确保追踪速度快，效率高。

附图说明

下面结合附图及实施例对本发明作进一步描述：

图1为发生局部遮挡的光伏组串的示意图；

图2为光伏组串的i-v曲线和p-v曲线。

图3为发生局部遮挡的光伏阵列在第一种情况下的电气特性；

图4为图3所述第一种情况下的i-v曲线；

图5为发生局部遮挡的光伏阵列在第二种情况下的电气特性；

图6为图5所述第二种情况下的i-v曲线；

图7为发生局部遮挡的光伏阵列在第三种情况下的电气特性；

图8为图7所述第三种情况下的i-v曲线；

图9为光伏组串的i-v曲线及其等效划分区间的示意图；

图10为光伏系统原理图；

图11为仿真结果的示意图。

具体实施方式

当光伏组串发生如图1所示的局部遮挡时，根据其工作状态，可分为三种情况。

1.当moduleb和modulec因被旁路二极管短路而停止工作时，其电气特性表现为两个独立的电压源vd，如图3所示。此时，由于光伏组串电流istring主要由modulea来提供，因此光伏组串的i-v特性主要由modulea主导，如图4所示。

2.同理，当仅有modulec因被旁路二极管短路而停止工作时，其电气特性同样表现为一个独立的电压源vd，如图5所示。此时，由于modulea表现为一个线性电压源vs，整个光伏组串的特性主要由moduleb主导，如图6所示。

3.同理，当所有module都正常工作时，modulea和moduleb同时表现为一个线性电压源vs，如图7所示，整个光伏组串的特性主要由modulec主导，如图8所示。

根据上述分析不难看出，当光伏组串发生局部遮挡时，其i-v特性在不同阶段，分别由不同module所主导。此时，我们只需要追踪此主导module，便可以追踪到其对应的峰值mpp。在此，我们定义一个新的变量，即光伏组串的等效主导电压(vdomi)，其可写为

vdomi＝vstring-(n-1)×vs+(m-n)×vd(1)；

其中vstring为整个光伏组串的输出电压，m为光伏组串的module数量，n则由

其中，voc为光伏组件的开路电压，α为变量，其值一般设在0.8到0.95之间。本文采用0.95。

公式(1)中，vd为旁路二极管压降，本文设定为0.8v。vs为线性直流电压源，其近似可由

其中vmpp,stc、impp,stc为光伏组件在标准测试环境下(standardtestcondition，stc)位于mpp点的电压电流值，voc,stc为光光伏组件在stc下的开路电压。

根据公式(1)-(3)，我们可以将整个光伏组串的i-v曲线，如图9第一行的曲线线所示，进行划分，其结果如图9第二行的曲线所示。此时，为了能够更快更准地追踪mpp，我们接着引用一个变量βdomi，即

其中c＝q/(nsakt)是光伏特性参数。根据公式(4)，可将图9第二行的曲线进一步进行划分，即为图9第三行的曲线部分。从图9第三行的曲线部分可以看出，所有的峰值，包括lmpp和gmpp，均在βmax和βmin范围内。此时，只需要采用传统的beta法，分别对这三个区间进行追踪，即可求出整个光伏组串的gmpp。

如图10所示，本发明的系统结构图，其中包括了光伏阵列、dcdc变换器和mppt跟踪模块。其中太阳能阵列模拟器(pvemulator)用来模拟光伏阵列的输出，dspace用来完成本算法的实现。

实验结果如图11所示。

上述实施例只为说明本发明的技术构思及特点，其目的在于让熟悉此项技术的人能够了解本发明的内容并据以实施，并不能以此限制本发明的保护范围。凡根据本发明主要技术方案的精神实质所做的修饰，都应涵盖在本发明的保护范围之内。