基于模糊变结构的超声速飞行器过载指令快速跟踪方法与流程

本发明属于飞行器控制技术领域，涉及一种基于模糊变结构的超声速飞行器过载指令快速跟踪方法。

背景技术：

高超声速飞行器的控制问题在世界各军事强国中引起了广泛的关注，尤其是随着超声速导弹、飞机、高超声速导弹、运载器的发展，其军事应用价值吸引了各军事强国投入大量的人力物力开展研究。而过载控制则是在很多对机动性要求的空空导弹中早有应用，当然相对来说，姿态控制体系的发展更为成熟，应用也更为广泛。而在飞行器控制算法上，PID控制无疑是应用最为广泛的算法之一，但随着飞行器速度与外形越来越复杂，很多时候PID控制设计方法已无法满足其设计要求，或者算法稳定裕度不足，或者算法过于保守使得快速性不好。因此越来越多的学者尝试采用非线性控制方法甚至智能控制方法来改善高超声速飞行器的控制系统设计。变结构控制无疑是众多非线性控制算法中最具有发展前景的方法之一，而模糊控制作为智能控制方法之一，也由于其良好的物理意义而广泛应用于工业控制之中。

超声速飞行器的过载控制在很多对机动性要求比较高的空空导弹中早有应用，但其控制难点在于非最小相位特性使得传统的PID控制在某些特征点难以保证系统稳定。

技术实现要素：

为实现上述目的，本发明提供一种基于模糊变结构的超声速飞行器过载指令快速跟踪方法，实现了对给定过载信号的快速跟踪，保证超声速飞行器俯仰通道过载控制的稳定性。

本发明所采用的技术方案是，基于模糊变结构的超声速飞行器过载指令快速跟踪方法，按照以下步骤实施：

步骤1，测量飞行器纵向过载误差、俯仰角速度与俯仰角加速度；

步骤2，采用纵向过载误差信号，设计过载、角加速度与角速度混合的滑模面信号s；

步骤3，针对滑模面信号s构造非线性滑模控制量δ_z；

步骤4，构造模糊系统，建立控制律增益与参数的模糊调整规则；

步骤5，飞行器俯仰通道过载控制的建模与数字仿真模拟；

步骤6，将步骤1-4所得到的结果，输入步骤5建立的超声速飞行器俯仰通道简化模型，通过选取合适的滑模面参数、模糊系统参数、控制增益参数，并观察输出曲线，从而确定最终的基于模糊变结构的超声速飞行器过载指令跟踪控制器参数，使得整个飞行器俯仰通道过载控制器具有满意的稳定性与响应速度。

进一步的，所述步骤1，按照以下步骤进行：将加速度计、俯仰角速率陀螺仪、角加速度计安装在飞行器器体上，其中采用加速度计测量飞行器的纵向过载，记为n_y，采用俯仰角速率陀螺仪测量飞行器俯仰角速度，记为ω_z，采用角加速度器测量飞行器俯仰角加速度，记为将纵向过载值n_y与飞行器纵向过载指令进行比较，得到纵向过载误差，记作e，其满足

进一步的，所述步骤2，设计的滑模面信号s为：

其中c₀、c₁、c₂、c₃、c₄、c₅与c₆为待设计的正参数，c₀、c₁、c₂、c₃、c₄、c₅与c₆为滑模面参数，均为增益，需要在后面设计中进行选定与调整，t为时间，∫edt为对e的积分。

进一步的，所述步骤3，构造的非线性滑模控制量δ_z为：

其中ε、ε₁、k₁、k₂、k₃、k₄为待设计的正参数，ε、ε₁、k₁、k₂、k₃、k₄为控制量参数，k₁、k₂、k₃、k₄为增益，需要在后面设计中进行选定与调整，ε、ε₁为柔化系数，用于减弱系统颤振。

进一步的，所述步骤4具体按照以下步骤进行：

首先，以e为模糊系统的输入，滑模控制中增益k₂为模糊系统的输出，建立输入输出变量的隶属度函数，用如下数学表达式描述：

选取d₁＝3，认为过载误差e属于‘PB’即‘正大’的范围，其隶属概率函数p₅为

认为误差e属于‘PM’即‘正中’的范围，其隶属概率函数p₄为

认为误差e属于‘ZO’即‘几乎为零’的范围，其隶属概率函数p₃为

认为误差e属于‘NM’即‘负中’的范围，其隶属概率函数p₂为

认为误差e属于‘NB’即‘负大’的范围，其隶属概率函数p₁为

系统输入输出的模糊集分别定义如下：

e＝{NB NM ZO PM PB}

dk₂＝{NB NM ZO PM PB}

其中，NB为误差“负大”的范围，NM为误差“负中”的范围，ZO为误差“几乎为零”的范围，PM为误差“正中”的范围，PB为过载误差“正大”的范围，dk₂为增益k₂的变化量；

其次，建立模糊调整的基本原则为：|e|越大，则飞行器控制量u应当越大，从而dk₂也应当越大；

设计模糊规则库如下：

R1：IF eis PB Then dk₂is PB

R2：IF eis PM Then dk₂is PM

R3：IF eis ZO Then dk₂is ZO

R4：IF eis NM Then dk₂is PM

R5：IF eis NB Then dk₂is PB

并设计规则矩阵如下：

最后，采用Matlab软件的newfis('smc_fz_2')函数生成模糊系统，再采用addrule函数将上述规则矩阵加入模糊系统，然后利用函数a1＝setfis(a1,'DefuzzMethod','centroid')设置采用centroid方法反模糊化，使用evalfis(abs(e),a1)函数，反解模糊滑模控制的增益调节规律，得到dk₂；

k₂＝k₂₀+dk₂

其中，k₂₀为增益k₂的初始值；

采用同一模糊系统，对参数c₁进行调节，调节规律如下

c₁＝c₁₀+0.05*dk2

其中，c₁₀的含义是参数c₁的初始值；

采用如下Matlab程序实现c₁的调节：c₁＝c₁₀+0.05*evalfis(abs(e),a1)。

本发明的有益效果是，本发明综合运用了变结构控制与模糊控制的优点，提出了一类复杂的非线性模糊变结构控制策略，较之传统的PID控制方法，使得过载跟踪的响应速度较快，具有很好的稳定性，同时系统震荡因模糊策略的引入而消弱，而使得其颤振问题得到了很好的抑制。因此本发明不仅在理论上具有很强的创新性，而且由于模糊控制的引入，使得其在工程上也具有很好的实用性，也推动了高超声速飞行器的智能控制技术向前进一步发展。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1是本发明提供的一种基于模糊变结构的超声速飞行器过载指令快速跟踪方法原理框图。

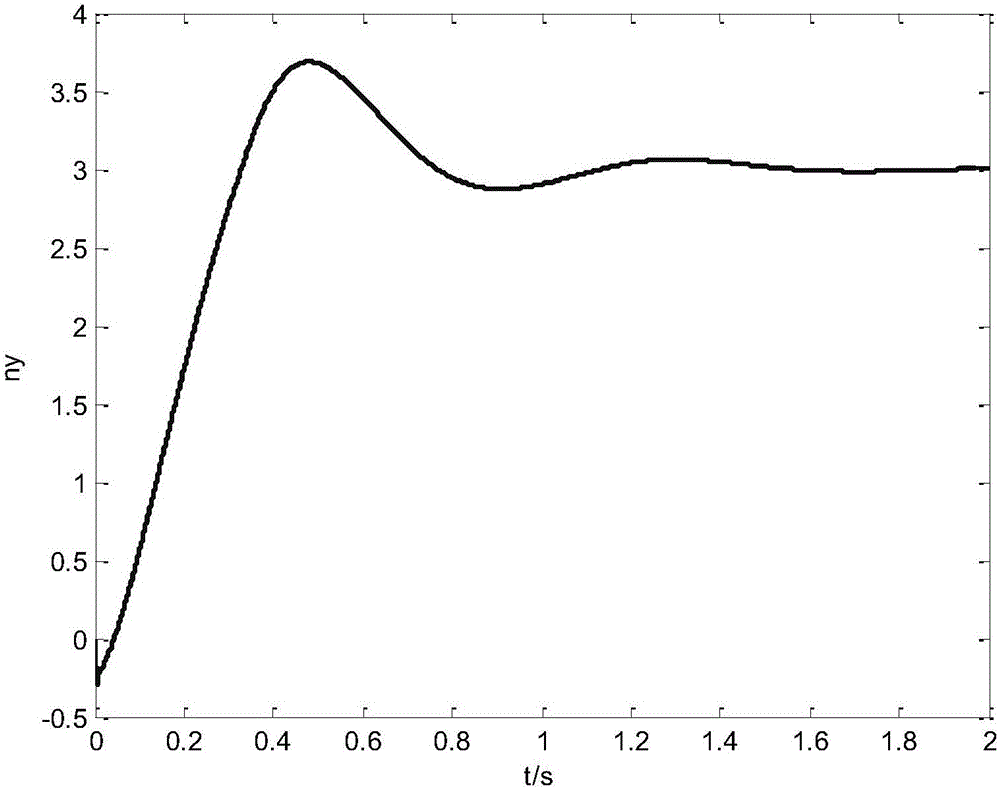
图2是本发明实施例所提供方法的超声速飞行器过载响应曲线。

图3是本发明实施例提供方法的超声速飞行器攻角曲线。

图4是本发明实施例提供方法的超声速飞行器舵偏角曲线。

图5是本发明实施例提供方法的超声速飞行器角速度曲线。

图6是本发明实施例提供方法的超声速飞行器角加速度曲线。

图7是本发明实施例提供方法的超声速飞行器滑模面曲线。

图8是本发明实施例提供方法的超声速飞行器增益模糊调节曲线。

图9是本发明实施例提供方法的误差e的隶属度函数。

图10是发明实施例提供方法的增益k₂变化量的隶属度函数。

具体实施方式

下面将结合本发明实施例中，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明首先采用线加速度计、陀螺仪与角加速度计对超声速飞行器的纵向过载、俯仰角速度、俯仰角加速度进行测量，与期望的过载指令信号进行反馈与比较得到过载误差信号，其次通过过载误差信号与角速度以及角加速度的测量信号构造一类复杂非线性滑模面，然后针对误差信号与滑模面，设计模糊滑模控制律。建立模糊系统，按照误差绝对值越大控制增益越大的原则建立模糊规则库与规则矩阵，最后采用反模糊化方法解算出滑模控制的增益，同时利用该模糊系统对滑模面参数进行模糊调节。最终实现对给定过载信号的快速跟踪，保证超声速飞行器俯仰通道过载控制的稳定性。原理图如图1所示。

步骤一：测量飞行器纵向过载、俯仰姿态角速度与俯仰姿态角速度。

将加速度计、俯仰角速率陀螺仪、角加速度计安装在飞行器器体上，其中采用加速度计测量飞行器的纵向过载，记为n_y，采用俯仰角速率陀螺仪测量飞行器俯仰角速度，记为ω_z，采用角加速度器测量飞行器俯仰角加速度，记为

将纵向过载值n_y与飞行器纵向过载指令进行比较，得到纵向过载误差，记作e，其满足

步骤二：采用上述过载误差信号，设计一类复杂的过载、角加速度与角速度混合滑模面信号s，

其中c₀、c₁、c₂、c₃、c₄、c₅与c₆为待设计的正参数。c₀、c₁、c₂、c₃、c₄、c₅与c₆为滑模面参数，均为增益，需要在后面设计中进行选定与调整。

t为时间，∫edt为对误差信号e积分。

步骤三：针对上述滑模面信号，构造非线性滑模控制量δ_z如下：

其中ε、ε₁、k₁、k₂、k₃、k₄为待设计的正参数。ε、ε₁、k₁、k₂、k₃、k₄为控制量参数，k₁、k₂、k₃、k₄为增益，需要在后面设计中进行选定与调整。ε、ε₁为柔化系数，用于减弱系统颤振。

步骤四：构造模糊系统，建立上述控制律增益与参数的模糊调整规则：

首先，以过载误差e为模糊系统的输入，滑模控制中增益k₂为模糊系统的输出，建立输入输出变量的隶属度函数，该隶属度函数就是图9所描述，可用如下数学表达式描述：

选取d₁＝3，认为过载误差e属于‘PB’即‘正大’的范围，其隶属概率函数p₅为

认为误差e属于‘PM’即‘正中’的范围，其隶属概率函数p₄为

认为误差e属于‘ZO’即‘几乎为零’的范围，其隶属概率函数p₃为

认为误差e属于‘NM’即‘负中’的范围，其隶属概率函数p₂为

认为误差e属于‘NB’即‘负大’的范围，其隶属概率函数p₁为

属于模糊控制中的基本函数与概念。

系统输入输出的模糊集分别定义如下：

e＝{NB NM ZO PM PB}

dk₂＝{NB NM ZO PM PB}

其中，NB为误差“负大”的范围，NM为误差“负中”的范围，ZO为误差“几乎为零”的范围，PM为误差“正中”的范围，PB为过载误差“正大”的范围。

上式中e为过载误差；dk₂为增益k₂的变化量。

如图9，PB为过载误差‘正大’的范围，如图所示，大约为3至9为正大的范围，概率随着误差的增大而增大至1，当过载误差大于9时，认为过载误差属于正大的概率为100％。PM为误差‘正中’的范围，ZO为误差‘几乎为零’的范围，NB为误差‘负大’的范围，NM为误差‘负中’的范围，其具体范围与概率分布见图中所示。

如图10所示，PB为增益dk₂‘正大’的范围，大约为0.1至0.3为正大的范围，概率随着误差的增大而增大至1，当增益大于0.3时，认为增益属于正大的概率为100％。PM为增益‘正中’的范围，ZO为增益‘几乎为零’的范围，NB为增益‘负大’的范围，NM为增益‘负中’的范围，其具体范围与概率分布见图中所示。

其次，建立模糊调整的基本原则为：|e|越大，则飞行器控制量u应当越大，从而dk₂也应当越大。

设计模糊规则库如下：

R1：IF eis PB Then dk₂is PB

R2：IF eis PM Then dk₂is PM

R3：IF eis ZO Then dk₂is ZO

R4：IF eis NM Then dk₂is PM

R5：IF eis NB Then dk₂is PB

并设计规则矩阵如下：

最后，采用Matlab软件的newfis('smc_fz_2')函数生成模糊系统，再采用addrule函数将上述规则矩阵加入模糊系统，然后利用函数a1＝setfis(a1,'DefuzzMethod','centroid')设置采用centroid方法反模糊化，使用evalfis(abs(e),a1)函数，反解模糊滑模控制的增益调节规律，得到dk₂；

k₂＝k₂₀+dk₂

k₂₀为增益k₂的初始值。

采用同一模糊系统，对参数c₁进行调节，调节规律如下

c₁＝c₁₀+0.05*dk2

c₁₀的含义是参数c₁的初始值。

采用如下Matlab程序实现c₁的调节：c₁＝c₁₀+0.05*evalfis(abs(e),a1)。

为了确保上述步骤一至步骤四中控制器参数选取合理，可用通过计算机数字仿真的手段进行编程模拟，从而验证本发明控制方法的正确性与合理性，以方便进行参数调整。

步骤五：飞行器俯仰通道过载控制的建模与数字仿真模拟

以一类超音速飞行器俯仰通道过载控制的简化数学模型为例，进行数字仿真分析，以验证本发明提供的控制方法的正确性、有效性与合理性。某类超声速飞行器俯仰通道的简化线性模型可以采用如下微分方程来近似描述：

其中α为飞行器俯仰通道攻角。n_y、ω_z与的定义见前文，δ_z为飞行器俯仰舵偏角(本文是使得该舵偏角按照前面采用非线性滑模控制设计的规律来变化，就可以实现攻角跟踪的控制总目的，因此此处δ_z为飞行器俯仰舵偏角；但具体到本专利方法，又称其为非线性滑模控制律)。a₂₄、a₂₅、a₂₂、a₃₅、a₃₄为飞行器的俯仰通道气动参数标称值，为风洞实验测量所得。v为飞行速度，g为重力加速度。

的含义是攻角的导数。

步骤六：将步骤一至步骤四所得的控制器，输入步骤五所建立的超声速飞行器俯仰通道简化模型，通过选取合适的滑模面参数、模糊系统参数、控制增益参数，并观察输出曲线，从而确定最终的基于模糊变结构的超声速飞行器过载指令跟踪控制器参数，使得整个飞行器俯仰通道过载控制器具有令人满意的稳定性与响应速度。

案例实施与计算机仿真模拟结果分析：

选取超声速飞行器俯仰通道的气动参数如下所示：

a₂₅＝-167.87，a₃₅＝-0.243，a₂₄＝-193.65，a₂₂＝-2.876，a₃₄＝1.584，v＝680.81，g＝9.810，设置期望的过载指令值为

选取滑模面参数为参数c₀＝0.02，c₁₀＝0.08，c₁＝c₁₀+0.05*dk2，c₂＝-0.4，c₃＝0.005，c₄＝0.005，c₅＝0.002，c₆＝-0.02。

设计控制增益参数为ε＝0.5、ε₁＝0.2、k₁＝-0.1、k₂₀＝-0.5、k₂＝k₂₀+dk2、k₃＝-0.05、k₄＝-0.2，系统初始状态均为0。将步骤三与步骤四所得到的控制器代入步骤五所示的简化模型进行仿真，得到仿真结果图2至图8所示。

由图2可以看出，采用本专利所示方法，超声速飞行器的过载跟踪响应速度非常快，上升时间大约为0.25s作用，稳态误差比较小。图3为超声速飞行器攻角曲线，由图可看成全程攻角均小于6度，满足工程小攻角要求，图4为超声速飞行器舵偏角曲线，全程远小于30度，未进入饱和区，故满足工程需求，图5与图6为超声速飞行器角速度曲线与角加速度曲线，由图可看出全程角速度变化比较平稳，无抖动与颤振。图7为模糊滑模控制中的滑模面曲线，由图可看出受滑模面参数模糊调节的影响，滑模面并没有完全收敛到0，但并不影响过载控制精度。图8为增益根据误差模糊调节的变化曲线，图8中可以看出增益随着误差的变化而模糊变化。

从以上案例仿真结果可以看出，本发明提供的基于模糊变结构的飞行器过载指令快速跟踪方法在原理上是完全正确与可行的，能够准确地对飞行器给定期望过载指令进行稳定跟踪，实现超音速飞行器俯仰通道的稳定控制。同时由于非线性滑模面的设计，与模糊参数调节的引入，使得系统具有很好的快速性，而模糊算法的引入又能较好地消除滑模控制引起的颤振问题。因此，本发明所提供的算法具有良好的稳定性与动态性能，不仅具有理论创新性，而且具有很高的工程实用价值。

以上所述仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内所作的任何修改、等同替换、改进等，均包含在本发明的保护范围内。