基于滑模补偿器技术的线控转向系统控制方法与流程

本发明属于车辆工程领域的线控转向技术，具体涉及一种基于滑模补偿器技术的线控转向系统控制方法。

背景技术：

线控转向系统的核心是转向性能对参数变化、外部干扰和道路条件的变化是否保持鲁棒性，虽然传统的比例微分控制的转向性能是可以接受的，然而对控制器的设计应为线控转向系统实现良好的转向性能，尤其是当道路条件具有大不确定性和不可预知的变化。

为此，人们做出了各种努力，如题为“steeringcontrolofmotorcyclesusingsteer-by-wiresystem”,y.marumoandm.nagai,veh.syst.dyn.vol.45,no.9,pp.445–458,2007.(“线控转向系统的摩托车转向控制方法”，y.marumoandm.nagai,《车辆系统动力学》，2007年第45卷第9期445-458页)的文章,该文提出了状态反馈控制方案，采用线性二次型技术提出了驾驶摩托车搭载的线控转向系统的转向角跟踪参考转向信号，然而，此传统反馈控制的缺点是，闭环系统可以稳定附近的平衡，但当有大不确定性道路条件时并不能保证闭环性能。

题为“implementationanddevelopmentofanadaptivesteering-controlsystem”，a.e.cetin,m.a.adliandd.e.barkana,ieeetrans.veh.technol,vol.59,no.1,pp.75–83,2010.(“自适应转向控制系统的实现与开发”，a.e.cetin,m.a.adliandd.e.barkana.《ieee学报-车辆技术期刊》，2010年第59卷第1期75-83页)的文章,该文提出了自适应极点配置控制器被用来减少跟踪误差，但是，一个实际的问题是，在参数估计中没有考虑道路条件对转向性能的影响。

综上，现有的线控转向系统控制方法还存在如下问题：

1、pid控制简单易懂，使用中不需精确的系统模型等先决条件，可是存在着信号处理太简单，控制精度不足的问题；

2、h∞控制在控制理论、控制方法及应用等方面，经过多年的发展，已成为一种具有较完整体系的鲁棒控制理论，可是存在着诸如理论复杂、计算量大和参数摄动范围有限等问题；

因此，本领域需要一种能够实现在线控转向系统中克服大不确定性和不同道路条件影响并具有强鲁棒性的控制方法，以提升车辆的转向性能。

技术实现要素：

本发明要解决的技术问题为克服现有技术中控制器的跟踪性能鲁棒性不强及控制器的跟踪误差控制精度低的不足，提供一种基于滑模补偿器技术的线控转向系统控制方法。

本发明的目的是这样实现的，本发明提供了一种基于滑模补偿器技术的线控转向系统控制方法，包括前轮转角δf和方向盘转角θh的实时信号采集，其特征在于，主要步骤如下：

步骤1，令转向系统两个伺服驱动器均运行在转矩控制模式，实时采集前轮转角δf和方向盘转角θh；

步骤2，根据步骤1所得的前轮转角δf和方向盘转角θh，定义跟踪误差εθ＝δf-θhr，其中θhr为方向盘转动参考角，nθ是方向盘转角θh和前轮转角δf之间的比例因子；

步骤3，将步骤1采集到的前轮转角δf通过鲁棒微分器1得到前轮转角观测值的角速度将步骤2得到的方向盘转动参考角θhr通过鲁棒微分器2得到方向盘转动参考角观测值的角速度再将方向盘转动参考角观测值的角速度通过鲁棒微分器3得到方向盘转动参考角观测值的角加速度

步骤4，将步骤2得到的跟踪误差εθ、步骤3得到的前轮转角观测值的角速度和方向盘转动参考角观测值的角速度得到标称控制信号u1；将步骤2得到的跟踪误差εθ、步骤3得到的前轮转角观测值的角速度和方向盘转动参考角观测值的角速度给到滑模面上，得到滑模变量s；再将得到的滑模变量s、前轮转角δf和前轮转角观测值的角速度作为输入变量输入到滑模补偿器中，得到补偿器信号u0；

步骤5，根据步骤4中得到的补偿器信号u0和标称控制信号u1，并考虑线控转向系统中的不确定性，设闭环控制输入信号u由两部分组成，即u＝u0+u1；

步骤6，将步骤5中的闭环控制输入信号u传送到线控转向系统设备中给转向电机发送电压指令，控制车轮转动，得到理想前轮转角δ′f。

优选地，步骤1所述实时采集的采样周期δt＝0.001秒。

优选地，步骤3所述通过鲁棒微分器1得到前轮转角观测值的角速度通过鲁棒微分器2得到方向盘转动参考角观测值的角速度和通过鲁棒微分器3得到方向盘转动参考角观测值的角加速度的步骤分别如下：

前轮转角观测值的角速度的表达式为式中，v是前轮转角角速度估计值的鲁棒微分器输出，v1是鲁棒微分器1的中间变量，v1＝∫(-α1sign(σf))dt,t是积分时间变量，σf是鲁棒微分器1滑模变量，σf＝x-δf，x是前轮转角观测值，δf是前轮转角，α1是前轮转角系数1且是一个正常数，ζ1是前轮转角系数2且是一个正常数；

方向盘转动参考角观测值的角速度的表达式为式中，w是方向盘转动参考角角速度估计值的鲁棒微分器输出，w1是鲁棒微分器2的中间变量，w1＝∫(-α2sign(σhr))dt，t是积分时间变量，σhr是鲁棒微分器2滑模变量，σhr＝y-θhr，y是方向盘转动参考角观测值，θhr是方向盘转动参考角，α2是方向盘转动参考角系数1且是一个正常数，ζ2是方向盘转动参考角系数2且是一个正常数；

方向盘转动参考角观测值的角加速度的表达式为式中，q是方向盘转动参考角角加速度估计值的鲁棒微分器输出，q1是鲁棒微分器3的中间变量，t是积分时间变量，是鲁棒微分器3滑模变量，是方向盘转动参考角观测值的角速度，是方向盘转动参考角角速度，α3是方向盘转动参考角角速度系数1且是个正常数，ζ3是方向盘转动参考角角速度系数2且是个正常数。

优选地，所述的标称控制信号u1的表达式为：

式中，τfa0为系统扰动标称值1，其中，fs0是库伦摩擦常数的标称值，是前轮转角观测值的角速度，kr0是转向传动比的标称值；

τea0是在潮湿柏油路上的外部轮胎回正力矩，其中τe0是回正力矩的标称值，τdis0为系统扰动标称值2；

εθ是跟踪误差，是跟踪误差观测值的一阶微分值，其中，是前轮转角观测值的角速度，是方向盘转动参考角观测值的角速度；

a0为线控转向系统参数标称值1，其中，jeq0是总惯性系数的标称值，kr0是转向传动比的标称值；

b0为线控转向系统参数标称值2，其中，beq0是总阻尼系数的标称值，kr0是转向传动比的标称值；k1为控制增益1，k2为控制增益2。

优选地，所述滑模面中，滑模变量s被定义为：

式中，λ是滑模参数且它是一个正数，εθ是跟踪误差，是跟踪误差观测值的一阶微分值，其中，

优选地，所述的补偿器信号u0的表达式为：

式中，

a0为线控转向系统参数标称值1，其中jeq0是总惯性系数的标称值，kr0是转向传动比的标称值；

b0为线控转向系统参数标称值2，其中beq0是总阻尼系数的标称值，kr0是转向传动比的标称值，k1为控制增益1，k2为控制增益2；

λ是滑模参数且是一个正数，εθ是跟踪误差，是跟踪误差观测值的一阶微分值，其中，是前轮转角观测值的角速度，是方向盘转动参考角观测值的角速度；

q1是滑模补偿器系数1，q2是滑模补偿器系数2；

饱和函数sat(s)的定义为：δ表示滑模边界层厚度且δ>0，s为滑模变量，同时滑模变量s以δ为边界，

为集总不确定性2的上界，为集总不确定性1的上界，式中，其中，c0是滑模补偿器的集总不确定性系数1且是一个正常数，c1为滑模补偿器的集总不确定性系数2且是一个正常数，c2为滑模补偿器的集总不确定性系数3且是一个正常数，δf是前轮转角，是前轮转角观测值的角速度；

是方向盘转动参考角观测值的角加速度的上界，其中，γ0是方向盘模型系数1且是一个正常数，γ1是方向盘模型系数2且是一个正常数，γ2是方向盘模型系数3且是一个正常数，θhr是方向盘转动参考角，是方向盘转动参考角观测值的角速度。

本发明公开的基于滑模补偿器技术的线控转向系统控制方法，在系统具有大不确定性因素和不同的道路条件的影响下，实现了前轮转角密切跟踪方向盘转动参考角度的性能，具有强的鲁棒性和稳定性，其有益效果具体体现在：

1.所提出的基于滑模补偿器技术的线控转向系统控制方法在提供转向性能方面优于传统的边界层滑模控制器、h∞控制器，在应对系统的大不确定性和不同的道路条件时保持小的跟踪误差和强的鲁棒性。

2.滑动模态与对象参数和扰动无关，快速响应、对参数变化和扰动不灵敏，无须系统在线辨识，物理实现简单。

3.饱和函数滑模控制的车辆比符号函数滑模控制车辆先达到稳态，更加稳定，不会产生颤振现象。

附图说明

图1是本发明的线控转向系统控制结构图。

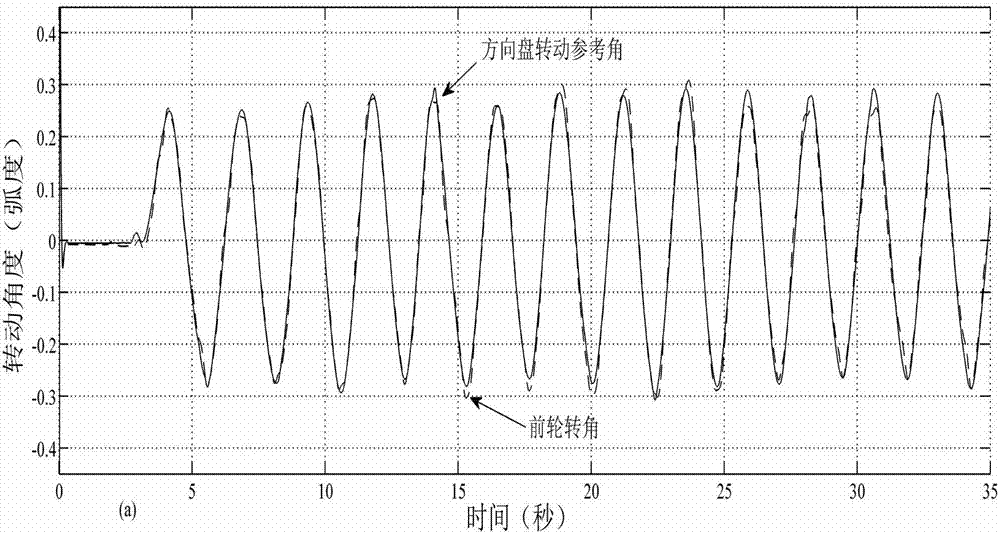
图2是本发明控制方法的跟踪性能曲线图。

图3是本发明控制方法的跟踪误差曲线图。

图4是本发明控制方法的控制转矩曲线图。

具体实施方式

下面将结合附图对本发明的技术方案进行清楚、完整的描述。显然所描述的实施例仅是本发明实施例的一部分，基于本发明的实施例，本领域的技术人员在没有做出创造性劳动的前提下获得的其它实施例，都属于本专利的保护范围。

本发明的实施例提供了一种基于滑模补偿器技术的线控转向系统控制方法，以解决现有技术中存在的跟踪误差大、鲁棒性不强和存在颤振的问题。

参见图1,基于滑模补偿器技术的线控转向系统控制方法，它包括前轮转角δf和方向盘转角θh的实时信号采集，其特征在于，主要步骤如下：

步骤1，令转向系统两个伺服驱动器均运行在转矩控制模式，实时采集前轮转角δf和方向盘转角θh。所述的实时采集的采样周期δt＝0.001秒。

步骤2，根据步骤1所得的前轮转角δf和方向盘转角θh，定义跟踪误差εθ＝δf-θhr，其中θhr为方向盘转动参考角，nθ是方向盘转角θh和前轮转角δf之间的比例因子。在本实施例中，取nθ＝12。

步骤3，将步骤1采集到的前轮转角δf通过鲁棒微分器1得到前轮转角观测值的角速度将步骤2得到的方向盘转动参考角θhr通过鲁棒微分器2得到方向盘转动参考角观测值的角速度再将方向盘转动参考角观测值的角速度通过鲁棒微分器3得到方向盘转动参考角观测值的角加速度

(1)通过鲁棒微分器1得到前轮转角观测值的角速度

式中，v是前轮转角角速度估计值的鲁棒微分器输出，v1是鲁棒微分器1的中间变量，v1＝∫(-α1sign(σf))dt,t是积分时间变量，σf是鲁棒微分器1滑模变量，σf＝x-δf，x是前轮转角观测值，δf是前轮转角，α1是前轮转角系数1且是一个正常数，ζ1是前轮转角系数2且是一个正常数。在本实施例中，取α1＝11，ζ1＝4。

(2)通过鲁棒微分器2得到方向盘转动参考角观测值的角速度

式中，w是方向盘转动参考角角速度估计值的鲁棒微分器输出，w1是鲁棒微分器2的中间变量，w1＝∫(-α2sign(σhr))dt，t是积分时间变量，σhr是鲁棒微分器2滑模变量，σhr＝y-θhr，y是方向盘转动参考角观测值，θhr是方向盘转动参考角，α2是方向盘转动参考角系数1且是一个正常数，ζ2是方向盘转动参考角系数2且是一个正常数。在本实施例中，取α2＝90，ζ2＝9；

(3)通过鲁棒微分器3得到方向盘转动参考角观测值的角加速度

式中，q是方向盘转动参考角角加速度估计值的鲁棒微分器输出，q1是鲁棒微分器3的中间变量，t是积分时间变量，是鲁棒微分器3滑模变量，是方向盘转动参考角观测值的角速度，是方向盘转动参考角角速度，α3是方向盘转动参考角角速度系数1且是个正常数，ζ3是方向盘转动参考角角速度系数2且是个正常数。在本实施例中，取α3＝90，ζ3＝9。

步骤4，将步骤2得到的跟踪误差εθ、步骤3得到的前轮转角观测值的角速度和方向盘转动参考角观测值的角速度得到标称控制信号u1；将步骤2得到的跟踪误差εθ、步骤3得到的前轮转角观测值的角速度和方向盘转动参考角观测值的角速度给到滑模面上，得到滑模变量s；再将得到的滑模变量s、前轮转角δf和前轮转角观测值的角速度作为输入变量输入到滑模补偿器中，得到补偿器信号u0。

(1)求标称控制信号u1。

式中，

τfa0为系统扰动标称值1，其中，fs0是库伦摩擦常数的标称值，是前轮转角观测值的角速度，kr0是转向传动比的标称值。在本实施例中，参数的选取主要考虑保持线控转向系统强鲁棒性和稳定性，取fs0＝3.04nm，kr0＝18。

τea0是在潮湿柏油路上的外部轮胎回正力矩，其中τe0是回正力矩的标称值，τdis0为系统扰动标称值2；

εθ是跟踪误差，是跟踪误差观测值的一阶微分值，其中，是前轮转角观测值的角速度，是方向盘转动参考角观测值的角速度；

a0为线控转向系统参数标称值1，其中，jeq0是总惯性系数的标称值，kr0是转向传动比的标称值；

b0为线控转向系统参数标称值2，其中，beq0是总阻尼系数的标称值，kr0是转向传动比的标称值，k1为控制增益1，k2为控制增益2。

在本实施例中,参数的选取主要考虑保持线控转向系统强鲁棒性和稳定性，取a0＝0.064，b0＝0.16，kr0＝18，k1＝-80，k2＝-15.5，kr0＝18。

(2)求滑模变量s

滑模变量s被定义为：

式中，λ是滑模参数且它是一个正数，εθ是跟踪误差，是跟踪误差观测值的一阶微分值，其中，在本实施例中，取λ＝12。

(3)求补偿器信号u0。

式中，

a0为线控转向系统参数标称值1，其中jeq0是总惯性系数的标称值，kr0是转向传动比的标称值。在本实施例中，取a0＝0.064，kr0＝18；

b0为线控转向系统参数标称值2，其中beq0是总阻尼系数的标称值，kr0是转向传动比的标称值，k1为控制增益1，k2为控制增益2。在本实施例中，取b0＝0.16，k1＝-80，k2＝-15.5，kr0＝18；

λ是滑模参数且是一个正数，εθ是跟踪误差，是跟踪误差观测值的一阶微分值，其中，是前轮转角观测值的角速度，是方向盘转动参考角观测值的角速度。在本实施例中，取λ＝12；

q1是滑模补偿器系数1，q2是滑模补偿器系数2。在本实施例中，取q1＝6，q2＝0.01；

饱和函数sat(s)的定义为：δ表示滑模边界层厚度且δ>0，s为滑模变量，同时滑模变量s以δ为边界，在本实施例中，取滑模边界层厚度δ＝0.1；

为集总不确定性2的上界，为集总不确定性1的上界式中，其中，c0是滑模补偿器的集总不确定性系数1且是一个正常数，c1为滑模补偿器的集总不确定性系数2且是一个正常数，c2为滑模补偿器的集总不确定性系数3且是一个正常数，δf是前轮转角，是前轮转角观测值的角速度。在本实施例中，取c0＝1.0，c1＝0.3，c2＝0.1；

是方向盘转动参考角观测值的角加速度的上界，其中，γ0是方向盘模型系数1且是一个正常数，γ1是方向盘模型系数2且是一个正常数，γ2是方向盘模型系数3且是一个正常数，θhr是方向盘转动参考角，是方向盘转动参考角观测值的角速度。在本实施例中，取γ0＝6，γ1＝2.8，γ2＝2.2。

步骤5，根据步骤4中得到的补偿器信号u0和标称控制信号u1，并考虑线控转向系统中的不确定性，设闭环控制输入信号u由两部分组成，即u＝u0+u1。

步骤6，将步骤5中的闭环控制输入信号u传送到线控转向系统设备中给转向电机发送电压指令，控制车轮转动，得到理想前轮转角δ′f。

图2是本发明控制方法的跟踪性能曲线图，图3是本发明控制方法的跟踪误差曲线图，图4是本发明控制方法的控制转矩曲线图。为验证本发明的实施效果，在线控转向系统实验平台中得到如图所示的控制效果图，从三个图中可看出本发明的控制方法可以使得前轮转角密切跟踪方向盘转动参考角度，减小了跟踪误差，增强了鲁棒性，改善了颤振现象。

以上依据图式所示的实施例详细说明了本发明的构造、特征及作用效果，其所述仅为本发明的较佳实施例，但本发明不以图面所示限定实施范围，凡是依照本发明的构想所作的改变，或修改为等同变化的等效实施例，仍未超出说明书与图示所涵盖的精神时，均应在本发明的保护范围内。