基于安排过渡过程的双向DC‑DC变换器控制方法与流程

本发明涉及一种双向dc-dc变换器控制方法，尤其涉及一种基于安排过渡过程的双向dc-dc变换器控制方法。

背景技术：

随着新能源产业的迅猛发展，储能系统的重要性日益显著。作为储能系统的关键部分，双向dc-dc变换器为系统的安全运行提供保障，其控制方式在电能储存过程中极其重要。双向dc-dc变换器常用控制方式为双闭环pid控制，但往往会导致控制器鲁棒性较弱，储能系统超调量与调节时间之间存在矛盾。

dc-dc变换器是储能系统的关键组成部分，其拓扑类型众多。为了保证储能系统的正常运行，对双向dc-dc变换器的控制也尤为重要。

技术实现要素：

发明目的：针对以上问题，本发明提出一种基于安排过渡过程的双向dc-dc变换器控制方法。

技术方案：为实现本发明的目的，本发明所采用的技术方案是：一种基于安排过渡过程的双向dc-dc变换器控制方法，具体包括以下步骤：

(1)采用系统辨识非参数建模描述双向dc-dc变换器动态特性，将变换器的阶跃响应特性曲线等效为线性二阶模型，计算需要辨识的系统参数；

(2)对原始pid控制器差分方程中的微分项和积分项采用后向差分近似，安排过渡过程；

(3)利用双向dc-dc变换器的过渡过程的加速度函数，最终获得安排的过程函数。

有益效果：本发明在利用辨识法获得变换器二阶线性模型传递函数的基础上，使用安排过渡过程的pid控制器对双向dc-dc变换器控制，安排过渡过程可以在变换器初始运行阶段消除输出电压电流的超调量，一定程度上解决了系统超调量与过渡时间之间的矛盾问题。

本发明采用基于安排过渡过程的新型双闭环pid控制方式，使储能系统在初始运行阶段消除输出超调量，将达到稳定的时间作为控制标准，实现系统无超调地达到稳定状态。

附图说明

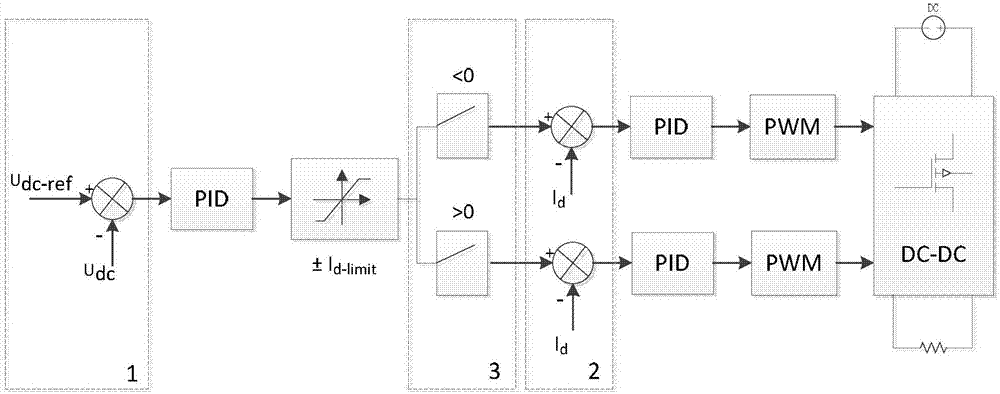
图1是双向dc-dc变换器框图；

图2是二阶传递函数零状态单位阶跃响应曲线图；

图3是双向dc-dc变换器传递函数matlab/simulink仿真曲线图；

图4是pid控制原理图；

图5是pid控制系统结构图；

图6是具有安排过渡过程的pid控制器模型图；

图7是安排过渡过程的单位阶跃响应效果图；其中，7(a)、7(b)为一对比组；7(c)、7(d)为一对比组；

图8是安排过渡过程的方波跟踪效果图；其中，8(a)为无过渡过程；8(b)为安排过渡过程；

图9是目标2a输出电流阶跃响应图；其中，9(a)为无过渡过程pid控制；9(b)为安排过渡过程pid控制。

具体实施方式

下面结合附图和实施例对本发明的技术方案作进一步的说明。

如图1所示是双向dc-dc变换器框图，其中，udc为双向dc-dc变换器的输出电压，id为锂电池充放电电流。根据双向dc-dc变换器在不同工作状态下控制对象的不同，采用双闭环控制策略，外环1控制输出电压，内环2控制充放电电流，如图虚线框所示，3为双向dc-dc变换器输出方向选择项。

采用系统辨识非参数建模描述双向dc-dc变换器动态特性，将变换器运行在某激励条件下的阶跃响应特性曲线近似等效为线性二阶模型，通常二阶线性模型传递函数如式(1)：

根据线性系统理论，纯延时不会改变系统特征参数。为使系统辨识过程方便简单，将系统作归一化处理，使式(1)变为式(2)：

其中，k为系统增益，ζ为系统阻尼系数，ωn为系统自然频率，τ为系统延时。式(2)经过拉普拉斯变换得到其在时域上的单位阶跃响应微分方程如式(3)：

其中，

二阶传递函数零状态单位阶跃响应曲线如图2所示。结合图2，根据二阶常系数微分方程特性，对式(3)求导，令导函数等于零可以求得：

其中，mn是t＝tn时刻y(t)的极大值。根据式(4)、(5)可以求出：

通过求解方程组可得需要辨识的系统参数，即自然频率ωn与系统阻尼系数ζ：

利用搭建好的双向dc-dc变换器驱动控制平台，测得双向dc-dc变换器动态响应曲线，增益归一化后如图3中虚线所示，图中可以看出，双向dc-dc变换器在约35ms时趋于稳定，前两次的超调量m0、m1，以及分别对应的时间t0、t1，代入式(7)，可以求得该激励条件下的系统特征参数ωn及ζ。通过matlab/simulink对双向dc-dc变换器传递函数进行仿真，仿真曲线如图3中实线所示，与实测曲线比较可以看到系统辨识的近似度较高，拟合效果好，可以满足绝大多数应用场合。

pid控制是基于被控变量的实际值与期望值的偏差，利用偏差量纠正系统的响应，执行调节控制，包括比例、积分、微分控制三个环节，控制原理如图4所示。因此根据pid控制原理可得出如下公式：

其中，kp、ki、kd分别为比例增益、积分增益和微分增益。比例环节的作用是加快系统的响应速度，提高系统的调节精度。积分环节的主要作用是消除系统的稳态误差。微分环节的主要作用是在响应过程中抑制系统偏差向任何方向进行变化，起到提前预知偏差变化的效果。将式(8)中的模拟信号数字化后，可得下式：

将式(9)与式(10)相减，可得到增量式pid的控制增量δu(k)：

δu(k)＝u(k)-u(k-1)

＝kp(e(k)-e(k-1))+kie(k)+

kd(e(k)-2e(k-1)+e(k-2))(11)

通过dsp芯片控制增量δu(k)，误动作影响小，不会产生积分失控，容易获得较好的速度调节效果。

pid控制系统结构如图5所示，在pid控制器中，微分环节的作用是抑制系统偏差向各个方向变化，能够有效改善系统的动态性能，但出现外界干扰时，会使得系统变得非常敏感。在双向dc-dc变换器实际运行时，电网电压及负载存在突变情况，变换器在电压电流控制过程中的微分项会将此视为干扰，产生较大的误差变化率，如果kd设置不当则可能引起系统失稳。此外，双向dc-dc变换器自身的响应比较快，调节时间短，因此更加需要对kd进行合理设计。结合电压电流采样电路，dsp通过采样值计算双向dc-dc变换器当前输出电压电流并将其作为反馈量，在cpu中执行控制算法产生新的pwm单元配置参数，输出相应的pwm驱动信号，从而保证双向dc-dc变换器工作状态稳定或完成双向dc-dc变换器工作状态的调整。

对原始pid控制器差分方程中的微分项和积分项采用后向差分近似的方法，差分方程可表示为：

其中，u(k)是pid控制器k时刻的输出；e是被控制量目标值减去实际值的差值；t是控制周期；ti是积分时间；td是微分时间；kp是比例系数；ki＝kpt/ti是积分系数；kd＝kptd/t是微分系数；up(k)是与当前差值成比例的比例控制量；ui(k)是与差值累积成比例的积分控制量；ud(k)是与前后差值变化率成比例的微分控制量。

对于偏差比例控制：

up(k)＝kpe(k)＝kp(s(k)-r(k))(13)

其中，s(k)是逐步接近最终目标值s0的一系列过渡目标值。通常，过渡目标值与实际值的差s(k)-r(k)要比最终目标值与实际值的差s0-r(k)小很多，因此，需要较大的比例系数获得足够的控制量。当被控量低于过渡目标值时，up(k)表现为正向激励；当被控量高于过渡目标值时，up(k)表现为负向激励。up(k)能够使得被控量跟踪过渡过程中各个目标值变化而变化。而在不安排过渡过程时，被控量始终与目标值比较，up(k)的切换并不及时。因此，安排过渡过程，提高了up(k)正负控制切换的及时性。

对于偏差积分控制：

其中，ε是设置了积分分离门限，k是控制周期。计算第k个控制周期的积分控制量时，如果前几个周期(l＝0，1，…，j-1)偏差大于积分分离门限，则积分量为0，当后几个周期(l＝j，j+1，…，k)偏差小于积分分离门限时，进行积分量的累积。如果没有安排过渡过程，被控量始终与最终目标值比较，积分控制只在被控量与最终目标差值小于积分分离门限时开始产生抑制作用，积分项的控制作用并不明显。安排过渡过程之后，被控量在每一个控制周期内都与逐步接近最终目标值的过渡目标值比较，如果偏差小于积分分离门限，积分控制起作用，参数设计的合理积分控制有可能全程都有效果。因此在安排了过渡过程之后，积分分离门限可以参考系统允许的稳态误差，设置小一些，积分系数也可以小一些。这样整个积分控制可以设计得比较温和。一般地动态误差主要靠比例项控制，静差则由积分控制消除。

对于偏差微分控制：

ud(k)＝kd(e(k)-e(k-1))

＝kd[(s(k)-r(k))-(s(k-1)-r(k-1))](15)

通常，微分控制总是抑制过程变化的趋势，即当没有安排过渡过程时，ud(k)与r(k)的变化趋势是相反的：

ud(k)＝kd[r(k-1)-r(k)](16)

而如果安排了过渡过程，式(16)可以改写为：

ud(k)＝kd(e(k)-e(k-1))

＝kd[(r(k)-r(k-1))-(s(k)-s(k-1))]＝δr-δs(17)

式(17)中的偏差量由两部分组成，第一部分是实际被控量的增量δr，第二部分是过渡目标的增量δs。当第一部分增量δr与第二部分增量δs相等时，说明被控量的变化等于安排的目标变化量，此时微分控制为零；当δr大于δs时，说明被控量的变化大于安排的目标变化量，此时微分控制表现为反向抑制作用；当δs大于δr时，说明被控量的变化小于安排的目标变化量，此时微分控制表现为正向推进作用。可见，安排过渡过程后，微分控制更为精细，它不再是简单地抑制过程的变化，而是既能使被控量接近目标值，又能使被控量远离目标值。

从上述安排过渡过程的影响可以看出，pid参数的选定范围扩大了。比例系数可以选择临界震荡比例系数，大一些或者小一些都满足要求；积分系数和微分系数可以由系统允许的稳态误差及控制周期确定，即期望在多少个控制周期内消除很小的误差，与实验法、经验法获取pid参数规律比较，更为简单快捷。

对于双向dc-dc变换器的二阶线性模型传递函数，过渡过程的加速度函数v2(t)：

其中，v0为设定值，t表示过渡过程时间。则速度函数v1(t)为加速度函数在时间t内的积分：

最终获得安排的过程函数v(t)：

一般地，加速度函数v2(t)可以按照如下规则选取：在区间(0，t)的前一部分取正，后一部分取负，正负面积相等即可。由于v1(t)在(0，t)上是为正，因此安排的过程v(t)是从零开始单调递增至v0的函数，没有超调。

根据双向dc-dc变换器系统的驱动时间和所能承受快慢的能力，选取过渡时间t，v0则为单位阶跃函数。利用matlab/simulink建立双向dc-dc变换器单位阶跃响应安排过渡过程后的pid控制器模型，如图6所示，matlabfun中即为安排的过渡过程，其输入为系统仿真时间，输出值与单位阶跃函数的乘积是不断接近最终目标值的过渡目标值。

在同一pid参数控制下，仿真曲线对比如下图7所示，7(a)、7(b)为一对比组，7(c)、7(d)为一对比组。通过对比在图中可以看出，安排过渡过程之后，被控量一直跟随逐步接近最终目标值的过渡目标值，因此系统在过渡时间内没有超调量，可以选取较大的比例增益系数，使系统快速响应，缩短系统达到稳定状态的时间。这样一来，系统超调量大小与过渡时间长短这一矛盾得到了解决，只需要将达到稳定的时间作为控制标准，系统可以无超调的达到稳定状态。

同样的方法和步骤，首先选取过渡时间t，v0选择为单位方波函数，通过matlab仿真，验证安排过渡过程对于双向dc-dc变换器开断的优化效果。在同一pid参数控制下，图8(a)是没有安排过渡过程的仿真曲线，从图中可以看出，在变换器开断阶段，存在一定的超调量，即输出电流切换的过渡时间内，电流不稳定；图8(b)是在0s、1s、2s三个时间点安排过渡过程后的仿真曲线，从图中可以看出，安排过渡过程后，变换器输出不再始终跟踪最终目标值，而是在安排的过渡时间内跟踪不断接近最终目标值的过渡目标值，因此在变换器开断阶段，输出没有产生超调的现象，而未安排过渡过程的其余时间，则存在超调量。

在仿真的基础上，利用双向dc-dc变换器的驱动平台，配合控制器及采样电路对变换器的恒流控制进行实际测试。通过设置驱动pwm波的频率和占空比，确定变换器输出电流。实验方案为变换器输出电流由1a向2a的阶跃响应，实验结果如图9(a)、(b)所示。从图中可以看出，安排过渡过程无法像仿真那样基本消除变换器输出电流的振荡，但可以在初始运行阶段，消除输出电流的超调量。