基于BA型五轴数控机床球头刀加工刀轴矢量光顺方法与流程

本发明涉及一种五轴数控机床刀轴矢量光顺方法，尤其涉及基于ba型五轴数控机床球头刀加工刀轴矢量光顺方法，属于五轴数控加工技术领域。

背景技术：

当使用球头刀五轴加工复杂曲面时，由于曲面几何性质较差，比如曲面的法向量、主方向、曲率等，容易导致所生成的球头刀刀轴矢量发生突变和大幅波动。即使采用最简单刀具定位方法(如sturz法)五轴加工上述曲面区域，也会引起刀轴矢量的剧烈变化，从而影响五轴机床运动的平稳性、超出机床进给轴的伺服能力和增大加工过程中的非线性误差等。因此获得五轴数控加工中球头刀光滑刀轴矢量成为曲面加工技术的重要研究方向。为获得光滑的刀轴矢量，国内外学者在刀轴矢量优化方面开展了大量研究工作，并提出许多五轴加工刀轴矢量优化方法，主要集中于两个方面：一是在工件坐标系中仅考虑几何约束的刀轴矢量优化方法；二是在工件坐标系中考虑几何约束和运动学约束的刀轴矢量优化方法。

现有技术一，文献(周波,赵吉宾与刘伟军,复杂曲面五轴数控加工刀轴矢量优化方法研究.机械工程学报,2013(07):184-192)提出一种复杂曲面五轴数控加工刀轴矢量优化方法。首先在非干涉域内有效插入限定的加工点位，保证刀轴矢量的整体优化；同时在干涉域内采用改进的c-space法，生成刀轴矢量光顺可行域。

现有技术二，文献(王晶等,复杂曲面零件五轴加工刀轴整体优化方法.航空学报,2013(06):1452-1462)提出一种基于临界约束的五轴刀轴矢量整体优化方法。首先构造了给定切触点处所有可行摆刀平面，并在摆刀平面内根据临界约束计算出临界刀轴矢量，在获得临界刀轴矢量的基础上，对其进行平面映射，建立了刀轴摆动的初始可行域；其次，通过对初始可行域进行均匀离散，根据离散点之间相对位置关系构造邻接矩阵，并结合最短路径搜索算法获得了初始参考刀轴，从而构造了新的刀轴摆动可行域；最后，建立当前切削行内无干涉且相邻刀轴变化最小的刀轴矢量优化模型，实现自由曲面五轴加工无干涉刀轴矢量的光滑控制。

上述现有技术至少存在以下缺点：

上述方法主要以刀具与工件/机床之间不发生过切和全局干涉等作为约束条件，以工件坐标系中刀轴矢量变化最小或光滑变化作为目标函数进行刀轴矢量优化，从而获得工件坐标系中无干涉和光滑的刀轴矢量。而五轴数控机床因结构差异较大，尽管工件坐标系中刀轴矢量光滑变化，却很难保证机床坐标系中五轴机床各坐标轴尤其是回转轴都能光滑运动而无突变现象发生，从而影响机床运动的平稳性、超出机床进给轴的伺服能力和增大加工过程中的非线性误差等。因此，有必要在工件坐标系中进行刀轴矢量优化时需考虑机床坐标系中机床回转轴的变化情况，或者在机床坐标系中直接对机床回转轴进行光顺优化。

技术实现要素：

为克服现有球头刀五轴加工复杂曲面刀轴矢量发生突变和大幅波动的问题，本发明提供一种基于ba型五轴数控机床球头刀加工刀轴矢量光顺方法。

为了实现上述目的，本发明采用的技术方案是这样的：一种基于ba型五轴数控机床球头刀加工刀轴矢量光顺方法，包括以下步骤：

a、建立球头刀刀轴矢量与刀位设计变量之间的关系方程；

b、建立球头刀刀轴矢量与五轴数控机床回转轴b和a之间的运动变换方程；

c、建立球头刀刀位设计变量和五轴数控机床回转轴b和a之间的关系方程；

d、确定球头刀刀轴矢量光顺的设计变量、目标函数和约束条件，建立基于ba型五轴数控机床球头刀加工刀轴矢量光顺数学模型；

e、确定步骤d中刀轴矢量光顺数学模型的求解方法。

作为优选：所述步骤a具体为：

(1)在刀触点处建立刀具局部坐标系，推导出局部坐标系olxlylzl中球头刀刀轴矢量与刀位设计变量之间的关系方程：

式中，θ为局部坐标系中球头刀绕yl轴转动的前倾角，ψ为局部坐标系中球头刀具绕xl轴转动的侧倾角，

在局部坐标系olxlylzl中球头刀刀触点处刀位点径矢

(2)建立工件坐标系中球头刀刀轴矢量与刀位设计变量之间的关系方程：

式中，e1＝(x1,y1,z1)^t，e2＝(x2,y2,z2)^t，e3＝(x3,y3,z3)^t分别为局部坐标系olxlylzl各坐标轴在工件坐标系owxwywzw中的单位矢量；

在工件坐标系owxwywzw中球头刀刀触点处刀位点径矢

作为优选：所述步骤b中，根据ba型五轴数控机床具体结构、机床运动链和机床各坐标系之间关系，建立球头刀刀轴矢量与五轴数控机床回转轴b和a之间关系方程：

作为优选：所述步骤c中，联立式(3)和(5)，则推导出球头刀刀位设计变量和机床回转轴b和a之间的关系方程：

作为优选：所述步骤d中，以机床坐标系中机床回转轴b和a作为设计变量，以曲面每行刀轨所有刀触点{pi,i＝1,…,n}处复合角加速度的平方和作为目标函数，以机床回转轴b和a的角度、角速度和角加速度限制范围作为约束条件，建立基于ba型五轴数控机床球头刀加工刀轴矢量光顺数学模型：

式中，n为给定行刀轨上刀触点数目，β1和β2分别代表机床回转轴b和a转角，ω1和ω2分别代表机床回转轴b和a角速度，α1和α2分别代表机床回转轴b和a加速度，和分别代表机床回转角β1和β2运动范围,和分别代表机床回转角β1和β2角速度限制范围,和分别代表机床回转角β1和β2角加速度限制范围，曲面上任意刀触点pi处的复合角加速度定义为：

式中，tpi(β1,β2)为刀触点pi处的刀轴矢量，t代表时间。

作为优选：所述步骤e具体为：

(1)利用现有球头刀五轴刀位优化方法生成给定曲面采样刀触点处的刀位，然后获得上述采样刀触点处的初始刀轴矢量；

(2)利用式(5)计算出各采样刀触点处所对应的机床回转角b和a，再利用三次样条插值函数分别将各采样刀触点处的机床回转角b和a进行三次样条拟合；

(3)利用步骤(2)所得到的三次样条插值拟合函数计算每行刀轨刀触曲线上各刀触点处机床回转角b和a，然后利用式(6)计算各刀触点处球头刀刀位设计变量θ和ψ，再利用式(4)和(3)计算出各刀触点处球头刀刀位点径矢和刀轴矢量，直到求解出该行刀轨刀触曲线上所有刀触点的刀位点径矢和刀轴矢量。

本发明的有益效果是，该方法能够避免机床回转轴突变和不光顺，使机床回转轴运动更加平稳和光滑，大幅减少机床回转轴的角速度和角加速度，从而提高曲面的加工质量和加工效率。

附图说明

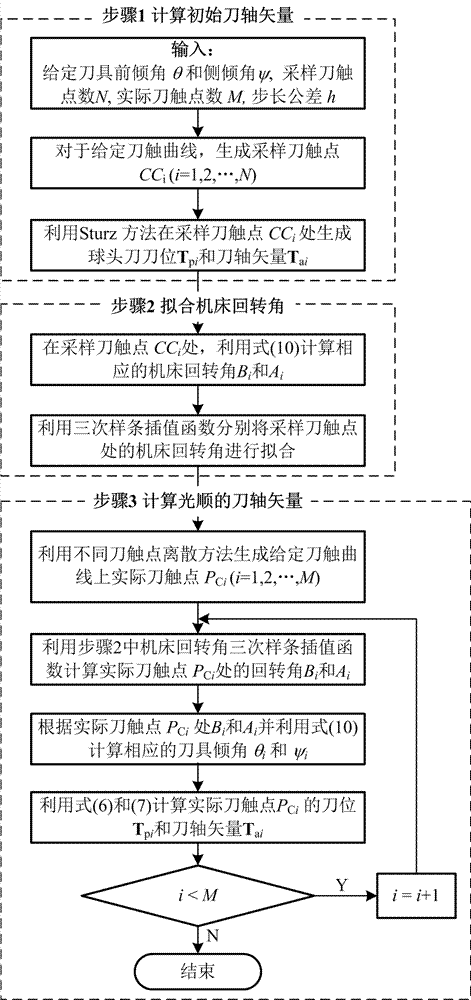
图1为基于ba型五轴数控机床球头刀加工刀轴矢量光顺方法流程图

图2为球头刀初步定位；

图3为ba′型五轴数控机床结构示意图；

图4为ba′型五轴数控机床中的坐标系；

图5为基于ba型五轴数控机床球头刀加工刀轴矢量光顺数学模型求解流程图。

具体实施方式

本发明的一种基于ba型五轴数控机床球头刀加工刀轴矢量光顺方法，其基本流程如图1所示，其较佳的具体实施方式是，包括：

步骤a、建立球头刀刀轴矢量与刀位设计变量之间的关系方程。所述步骤a具体为：

(1)局部坐标系中球头刀刀轴矢量与刀位设计变量之间的关系方程

如图1所示，设球头刀加工复杂曲面s：r(u,v)，pcc(ucc,vcc)为曲面上任意一点，ncc为该点的单位法矢，owxwywzw为工件坐标系。令r为球头刀的半径，ol为局部坐标系的原点，其中和分别为点ol和pcc对应的径矢。分别以ol为原点建立点pcc处的局部坐标系olxlylzl和刀具坐标系otxtytzt，且点ot与ol重合。假设初始状态时otxtytzt与olxlylzl的各坐标轴方向一致，则刀具在点pcc处被初步定位。在局部坐标系olxlylzl中，刀具存在两个自由度：一是绕yl轴旋转的前倾角θ，二是绕xl轴旋转的侧倾角ψ，以上两角即为刀位设计变量。

通过调整上述两个角度可以获得不同的刀位，可以得到局部坐标系olxlylzl中刀触点pcc处的刀轴矢量和刀位点径矢

式中，

由式(1)可得

由式(2)可得

(2)工件坐标系中球头刀具刀轴矢量与刀位设计变量之间的关系方程

假设局部坐标系olxlylzl各坐标轴在工件坐标系owxwywzw中的矢量分别为e1＝(x1,y1,z1)^t，e2＝(x2,y2,z2)^t，e3＝(x3,y3,z3)^t，则在工件坐标系owxwywzw中刀轴矢量和刀位点径矢为

由式(5)可得到球头刀刀位设计变量(即前倾角θ和侧倾角ψ)和刀轴矢量之间的关系方程

步骤b、建立球头刀刀轴矢量与五轴数控机床回转轴b和a之间的运动变换方程。所述步骤b具体为：

根据回转轴所在位置不同，ba型五轴数控机床又可以分为三种类型：1)ba型(b和a轴都位于主轴侧)，2)ba′型(a轴位于主轴侧和b轴位于转台侧)，3)b′a′型(b和a轴都位于转台侧)。为了简单起见，下文将以ba′型五轴数控机床作为研究对象进行阐述，其推导公式适用于所有ba型五轴数控机床，如图2所示。图3所示为ba′型五轴数控机床中各坐标系之间关系，一般默认工件坐标系owxwywzw与机床坐标系omxmymzm的坐标轴方向一致，数控系统可以将两者进行关联。由此可得，球头刀刀轴矢量与五轴数控机床回转轴b和a之间关系方程：

式中，

重新整理式(8)可得

步骤c、建立球头刀刀位设计变量和五轴数控机床回转轴b和a之间的关系方程。所述步骤c具体为：

将式(9)代入式(7)便得到球头刀刀位设计变量和五轴数控机床回转轴b和a之间的关系方程：

步骤d、确定球头刀刀轴矢量光顺的设计变量、目标函数和约束条件，建立基于ba型五轴数控机床球头刀加工刀轴矢量光顺数学模型。所述步骤d具体为：

(1)五轴加工中复合角加速度的定义

在机床坐标系中引入复合角加速度的概念，在设计曲面上任意刀触点pi处复合角加速度的定义为

式中，β1和β2分别代表机床回转轴b和a转角，为刀触点pi处的刀轴矢量，t代表时间，ω1和ω2分别代表机床回转轴b和a角速度，α1和α2分别代表机床回转轴b和a加速度。

(2)构建基于ba型五轴数控机床球头刀加工刀轴矢量光顺数学模型

以机床坐标系中机床回转轴b和a作为设计变量，以曲面每行刀轨所有刀触点{pi，i＝1,…,n}处复合角加速度的平方和作为目标函数，以机床回转轴b和a的角度、角速度和角加速度限制范围作为约束条件，建立基于ba型五轴数控机床球头刀加工刀轴矢量光顺数学模型：

式中，和分别代表机床回转角β1和β2运动范围,和分别代表机床回转角β1和β2角速度设置范围,和分别代表机床回转角β1和β2角加速度设置范围。

步骤e、确定步骤d中刀轴矢量光顺数学模型的求解方法。所述步骤e具体为：提出一种求解步骤d中刀轴矢量光顺的数学模型的方法，求解过程如图4所示，其具体过程如下：

(1)利用现有球头刀五轴刀位优化方法生成给定曲面采样刀触点处的刀位，然后获得上述采样刀触点处的初始刀轴矢量。

首先，通过分析加工曲面的特点，初步给定球头刀刀位设计变量的数值，即前倾角θ和侧倾角ψ，假设给定刀轨刀触曲线上采样刀触点数为n，实际刀触点数为m，给定步长公差为h。然后，在给定刀轨刀触曲线上利用等参数离散法生成采样刀触点{cci，i＝1,…,n}；最后，利用sturz法计算所有采样刀触点cci处刀轴矢量{tai，i＝1,…,n}和刀位点径矢{tpi，i＝1,…,n}。

(2)利用式(10)计算出各采样刀触点cci处所对应的机床回转角bi和ai，再利用三次样条插值函数将各采样刀触点cci处的机床回转角bi和ai进行三次样条拟合，从而得到机床回转角bi和ai的三次样条插值拟合函数f(u,b)和f(u,a)，其中u为采样刀触点的参数变量。

(3)对于给定刀轨刀触曲线，由给定m或h并利用等参数离散法或等弦高误差离散法生成实际刀触点{pci，i＝1,…,m}，再利用步骤(2)中三次样条插值拟合函数f(u,b)和f(u,a)计算该行刀轨刀触曲线上实际刀触点pci处所对应的机床回转角bi和ai；然后利用式(10)得到实际刀触点pci处机床回转角bi和ai所对应的球头刀刀位设计变量θi和ψi，进而由式(6)和(7)得到该刀触点pci处球头刀的刀位点径矢tpi和刀轴矢量tai，直到i＝m求解出该行刀触曲线上所有刀触点的刀位点和刀轴矢量。

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。