一种改进萤火虫算法的多无人机协同耦合任务分配方法与流程

本发明涉及任务规划设计领域，尤其是一种无人机协同作战的规划方法。

背景技术：

任务规划系统设计在很多领域的成功应用，为国防事业以及工业生产带来了很大提升，多无人机协同任务规划问题是一类具有多种约束的组合优化问题，也是一类典型的np-hard问题，具有高度复杂性。本发明以多无人机协同执行具有复杂耦合约束关系的sead任务为研究背景，充分考虑无人机的异构性、资源有限性以及任务间的耦合约束，包括确认、打击和毁伤评估三种子任务的时间耦合约束以及目标间的特殊耦合约束，以组合优化理论和新兴的优化算法为数学工具，对耦合任务环境下的多无人机协同任务规划问题进行深入研究。

萤火虫算法(fireflyalgorithm，fa)是由xin-sheyang于2008年提出的，它源自对自然界中萤火虫群体行为的模拟，是一种新兴的高级元启发式优化算法。该算法的优化机制是通过不同萤火虫个体之间的互相吸引达到寻找最优解的目的，因而是一种群智能(swarmintelligence)随机优化算法，其概念简单，流程清晰，需要调整的参数少，容易实现，因而受到众多国内外学者的关注。

萤火虫算法作为一种新兴的优化算法已在诸多领域展现了良好的应用前景，在任务规划系统设计领域的应用中，多数研究在建模时进行了一定程度的简化处理，并且没有考虑任务中存在的耦合约束关系，目前还没有文献将萤火虫算法及相关改进算法应用于同时具有时间耦合约束和特殊耦合约束的多无人机协同任务分配问题。

技术实现要素：

为了克服现有技术的不足，本发明提供一种具有特殊编解码结构的混合离散萤火虫算法，即de-dfa算法，根据对同时具有时间耦合约束和特殊耦合约束的多无人机协同任务分配问题进行研究，提出数学模型并进行任务解算。

本发明解决其技术问题所采用的技术方案的详细步骤如下：

步骤1：构建特殊耦合下的任务分配模型

在该步骤中，存在如下定义：

定义1：u＝{u1,u2,…,ui,…,um}为无人机集合，其中ui表示第i架无人机，m表示无人机总数；

定义2：t＝{t1,t2,…,tj,…,tn}为目标集合，其中tj表示第j个目标，n为目标总数；

定义3：taskjh为目标tj的第h种任务，h＝1,2,3，当h＝1为确认，h＝2为打击，h＝3为毁伤评估；

定义4：u^jh为能够执行任务taskjh的无人机集合；

定义5：tasksequencei＝{task1＞task2＞task3＞…＞taskni}为无人机ui的任务序列；其中ni表示分配给无人机ui的任务数量，taskni表示无人机ui需要执行的任务；

定义6：routei＝{upi,taskp1,taskp2,…,taskpni,b}为无人机ui的路径序列，taskpni表示无人机ui执行任务n时所在的位置，upi表示无人机i的初始位置，b表示无人机返回基地的位置；

定义7：voyi为无人机ui的航程，其中i＝1,2,…,m；

定义8：voymaxi为无人机ui的最大航程；

定义9：ri为无人机ui的武器载荷数量；

定义10：tijh为无人机ui执行任务taskjh消耗的执行时间；

定义11：stk为任务k的开始被执行时刻；

定义12：etk为任务k的完成时刻；

定义13：inter_min为打击任务和毁伤评估任务间的最小时间间隔；

定义14：inter_max为打击任务和毁伤评估任务间的最大时间间隔；

定义15：决策变量：

确认目标函数：选择无人机最大航程最短作为任务规划指标，该任务规划指标是将各无人机中的最大航程最小化，即目标函数为：

确认特殊耦合约束：特殊耦合约束指在在某一时刻，两个不同位置的目标同时被打击时，该约束针对同时执行且优先级如下面所述的两种目标，存在如下两种特殊耦合约束：

(1)任务同时执行约束：目标ti和目标tj必须同时打击，则有约束：

式(2)中，和inter分别表示目标ti的开始打击时刻、目标tj的开始打击时刻和打击目标ti和tj的时间间隔；

(2)任务优先级约束：目标tk必须在tl被确认之前被毁伤评估，则有约束：

式中，分别表示目标tk的毁伤评估结束时刻和目标tl的确认开始时刻；

具有复杂耦合约束下的多无人机任务分配数学模型：

步骤2：萤火虫编码

将萤火虫表示为1×2nt维数组，nt为所有任务数量，nt＝3×n，采用整数编码的形式，每个萤火虫分为两部分，前nt维表示任务分配部分，从左至右分别表示第i个目标的确认、打击和毁伤评估任务，即第1、2、3维代表第1个目标的确认、打击和毁伤评估任务，第4、5、6维代表第2个目标的确认、打击和毁伤任务，并以此类推，i＝1,2,…,n，每一维的取值由数组中每一维所对应任务的可执行无人机集合中的元素数量决定决定；后nt维表示任务排序部分，由3组所有目标的编号组成，从左至右，目标tj第h次出现分别对应该目标的确认、打击和毁坏评估任务，即目标tj第1次出现表示无人机i的确认，目标tj第2次出现表示无人机i的打击，目标tj第3次出现表示无人机i的毁伤评估；

步骤3：种群初始化

比较萤火虫之间的余弦相似度，当任意两只萤火虫余弦相似度超过设定的阈值ξ，则对其中一个萤火虫重新初始化，即对该萤火虫的数值随机化，其中阈值ξ取值在0.6-0.7之间，余弦相似度公式为：

其中，xi和xj分别指萤火虫i和萤火虫j所对应的向量；

步骤4：萤火虫位置更新

1)萤火虫位置进行β更新，具体步骤如下：

setp1：计算萤火虫xi和xj的海明距离hij，海明距离为两个萤火虫个体的位置向量中互相对应的数不相等的对数，并找到xi和xj中对应相等的元素；

setp2：计算xi对xj相对吸引度βij，其中hij为萤火虫i与萤火虫j的海明距离，γ是移动步长，β0表示在γ＝0处萤火虫的初始吸引力；

setp3：对于xi和xj中每一个不对应相等的元素ta，取随机数r，若r＜βij，则ta取xi和xj中对应元素的值，若r≥βij，则取xi和xj中本身对应元素的值；

2)在进行β更新后，萤火虫个体xj的任务排序部分tsj存在非法解，对萤火虫个体进行修正，具体修正步骤为：

a)令s1＝tsj、s2＝tsi、l＝length(s1)、p＝1、q＝1，tsi为萤火虫xi的任务排序部分，tsj为萤火虫xj的任务排序部分，l取萤火虫个体任务排序部分的长度，即任务总数；

b)找出s2中第一个等于s1(p)的元素的索引值p1，令s1(p)＝0，s2(p1)＝0，其中s1(p)为p值对应的s1；

c)令p＝p+1，若p≤l，则返回执行步骤b)，否则执行步骤d)；

d)若s1(q)不等于0，则在s2找到第一个非零元素的位置索引值p2，令s1(q)＝s2(p2)，s2(p2)＝0，其中s1(q)为q值对应的s1；

e)令q＝q+1，若q≤l，则执行步骤d)，否则结束；

3)进行α更新

在萤火虫算法中，α为步长因子，其公式为：

tai＝int(tai+α(rand-1/2))(5)

式(5)中，tai表示萤火虫任务分配部分某个元素的值，int是对参数取整操作，rand为随机因子；

4)对α更新后的编码进行非法修正，非法修正即为对每一位元素进行可行性判断：若元素的值在元素的取值范围内，则不用修正，若元素的值超出取值范围，则以距离边界值最近的点代替元素值；

步骤5：萤火虫个体重构

1)对于萤火虫个体的ts部分，采用基于邻域搜索的变异方法，其操作步骤如下：

step1：在个体的任务排序部分随机选择r个位，并生成其排序的所有邻域；

step2：计算所有邻域的目标函数，选出目标函数值最高的个体作为最佳个体，并代替原来的个体；

2)交叉操作

采用随迭代次数指数递增的交叉概率因子：

cr＝crmin+(crmax-crmin)×exp(-a×(1-t/t)^b)(6)

式(6)中，cr为交叉概率因子，crmin和crmax分别为最小交叉率和最大交叉率，且crmin＝0.4，crmax＝0.6；a＝40，b＝4，t为设定的最大迭代次数，t为当前迭代次数，交叉操作得到的新个体的取值为：

其中，为交叉操作得到的新个体，是需要交叉操作的个体，为不需要进行交叉操作的个体，jrand为随机数；

3)选择操作

在原始个体和经交叉操作后得到的新个体之间选择目标函数值大的个体保留到下一代，选择操作为：

其中，x^ti是第t代的第i个个体，u^ti是第t代经交叉后得到的个体，fitness为目标函数；

步骤6：特殊耦合约束的处理

用矩阵t^s∈r^3n×3n表示目标或任务间存在的特殊耦合约束关系，表示任务i与任务j的特殊耦合约束，其取值规则为：

步骤7：萤火虫个体解码与目标函数的计算

具体的解码步骤如下：

step1：对任务分配部分进行解码

(1)初始化各无人机的任务集合为空集，即

(2)从左至右依次读取萤火虫个体第k位上的值i，k＝1,2,…,2n，通过j＝fix(i/2)+1和h＝mod(i/2)分别得到j和h的值，将taskjh加入到tasksequencei中；

step2：对任务排序部分进行解码

(1)从左至右依次读取萤火虫个体第k位上的值j，k＝1,2,…,2n，每个j为目标tj上的一个任务，若j是第h次出现，则表示taskjh，当k＝2n得到所有任务的排列顺序tasks；

(2)将tasksequencei根据tasks重新排列任务顺序，当taskjh和taskkl均在tasksequencei中时，则以从左到右的顺序，若taskjh在tasks中的位置在taskkl前面，则yijhkl＝1，若taskjh在tasks中的位置在taskkl后面，则yijhkl＝-1；否则yijhkl＝0；

至此，解码结束，得到各无人机的任务执行序列tasksequencei。

本发明的有益效果在于具有较好的通用性，通过多次的仿真验证获得的数据分析，使得模型更加完善；迭代过程简短，收敛速度快；以最小化无人机的最大航程为整体优化目标，通过分段整数编码的方式有效地表示多无人机协同任务分配方案，并通过改进的de-dfa算法在解空间里寻找最优解，能够快速并有效地解决耦合任务环境下的多无人机任务分配问题，为解决耦合任务环境下的多无人机任务分配问题提供一种新的解决方案。

附图说明

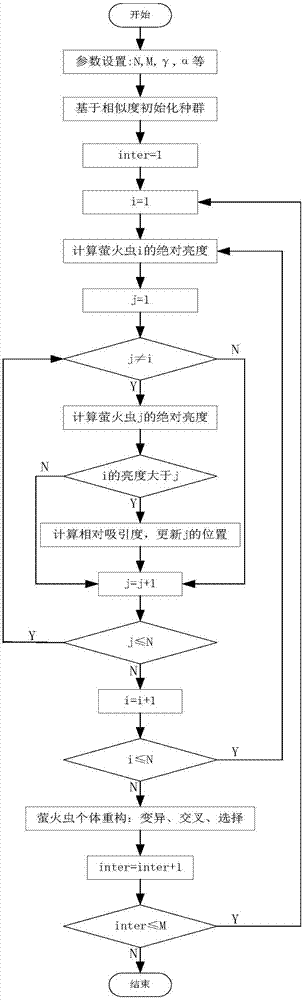
图1为本发明的de-dfa算法流程图。

图2为本发明的战场态势图。

图3为本发明的de-dfa算法收敛曲线。

图4为本发明的任务分配甘特图。

图5为本发明无人机执行任务过程的路径规划图，其中图5(a)为无人机1和无人机5执行任务时的路径规划图，图5(b)为无人机2和无人机4执行任务时的路径规划图，图5(c)为无人机3和无人机7执行任务时的路径规划图，图5(d)为无人机6执行任务时的路径规划图。

具体实施方式

下面结合附图和实施例对本发明进一步说明。

图1为本发明的de-dfa算法流程图，本发明的详细步骤如下：

步骤1：构建特殊耦合下的任务分配模型

在该步骤中，存在如下定义：

定义1：u＝{u1,u2,…,ui,…,um}为无人机集合，其中ui表示第i架无人机，m表示无人机总数；

定义2：t＝{t1,t2,…,tj,…,tn}为目标集合，其中tj表示第j个目标，n为目标总数；

定义3：taskjh为目标tj的第h种任务，h＝1,2,3，当h＝1为确认，h＝2为打击，h＝3为毁伤评估；

定义4：u^jh为能够执行任务taskjh的无人机集合；

定义5：tasksequencei＝{task1＞task2＞task3＞…＞taskni}为无人机ui的任务序列；其中ni表示分配给无人机ui的任务数量，taskni表示无人机ui需要执行的任务；

定义6：routei＝{upi,taskp1,taskp2,…,taskpni,b}为无人机ui的路径序列，taskpni表示无人机ui执行任务n时所在的位置，upi表示无人机i的初始位置，b表示无人机返回基地的位置；

定义7：voyi为无人机ui的航程，其中i＝1,2,…,m；

定义8：voymaxi为无人机ui的最大航程；

定义9：ri为无人机ui的武器载荷数量；

定义10：tijh为无人机ui执行任务taskjh消耗的执行时间；

定义11：stk为任务k的开始被执行时刻；

定义12：etk为任务k的完成时刻；

定义13：inter_min为打击任务和毁伤评估任务间的最小时间间隔；

定义14：inter_max为打击任务和毁伤评估任务间的最大时间间隔；

定义15：决策变量：

确认目标函数：选择无人机最大航程最短作为任务规划指标，该任务规划指标是将各无人机中的最大航程最小化，引导任务分配策略朝着最小化每架无人机航程的方向进行，即目标函数为：

确认特殊耦合约束：特殊耦合约束指在在某一时刻，两个不同位置的目标同时被打击时，该约束针对同时执行且优先级如下面所述的两种目标，存在如下两种特殊耦合约束：

(1)任务同时执行约束：目标ti和目标tj必须同时打击，则有约束：

式(2)中，和inter分别表示目标ti的开始打击时刻、目标tj的开始打击时刻和打击目标ti和tj的时间间隔；

(2)任务优先级约束：目标tk必须在tl被确认之前被毁伤评估，则有约束：

式(3)中，分别表示目标tk的毁伤评估结束时刻和目标tl的确认开始时刻；

具有复杂耦合约束下的多无人机任务分配数学模型：

步骤2：萤火虫编码

将萤火虫表示为1×2nt维数组，nt为所有任务数量，nt＝3×n，采用整数编码的形式，每个萤火虫分为两部分，前nt维表示任务分配部分，从左至右分别表示第i个目标的确认、打击和毁伤评估任务，即第1、2、3维代表第1个目标的确认、打击和毁伤评估任务，第4、5、6维代表第2个目标的确认、打击和毁伤任务，并以此类推，i＝1,2,…,n，每一维的取值由数组中每一维所对应任务的可执行无人机集合中的元素数量决定决定；后nt维表示任务排序部分，由3组所有目标的编号组成，从左至右，目标tj第h次出现分别对应该目标的确认、打击和毁坏评估任务，即目标tj第1次出现表示无人机i的确认，目标tj第2次出现表示无人机i的打击，目标tj第3次出现表示无人机i的毁伤评估；

如311232213依次表示执行无人机3的确认，无人机1的确认和打击，无人机2的确认，无人机3的打击，无人机2的打击和毁伤评估，无人机1的毁伤评估，无人机3的毁伤评估。

步骤3：种群初始化

选择随机产生的方式对萤火虫种群进行初始化，为了确保初始产生的萤火虫能较均匀地分布在解空间，从而防止种群过早陷入局部最优解，在随机初始化的过程中，比较萤火虫之间的余弦相似度，当任意两只萤火虫余弦相似度超过设定的阈值ξ，则对其中一个萤火虫重新初始化，即对该萤火虫的数值随机化，其中阈值ξ取值在0.6-0.7之间，余弦相似度公式为：

其中，xi和xj分别指萤火虫i和萤火虫j所对应的向量；

步骤4：萤火虫位置更新

1)萤火虫位置进行β更新，具体步骤如下：

setp1：计算萤火虫xi和xj的海明距离hij，海明距离为两个萤火虫个体的位置向量中互相对应的数不相等的对数，如两个萤火虫的位置向量分别是[2543618]、[2453816]，则它们的海明距离是4，并找到xi和xj中对应相等的元素；

setp2：计算xi对xj相对吸引度βij，其中hij为萤火虫i与萤火虫j的海明距离，γ是移动步长，β0表示在γ＝0处萤火虫的初始吸引力；

setp3：对于xi和xj中每一个不对应相等的元素ta，取随机数r，若r＜βij，则ta取xi和xj中对应元素的值，若r≥βij，则取xi和xj中本身对应元素的值；

2)在进行β更新后，萤火虫个体xj的任务排序部分tsj存在非法解，因为tsj部分是重复三次对目标进行排序，并以编号代替，所以每个目标均会且仅会出现三次，在β更新后，某些目标出现次数可能会少于3次，也有可能多于三次，这样的编码是不合理的，因而需要对萤火虫个体进行修正，具体修正步骤为：

a)令s1＝tsj、s2＝tsi、l＝length(s1)、p＝1、q＝1，tsi为萤火虫xi的任务排序部分，tsj为萤火虫xj的任务排序部分，l取萤火虫个体任务排序部分的长度，即任务总数；

b)找出s2中第一个等于s1(p)的元素的索引值p1，令s1(p)＝0，s2(p1)＝0，其中s1(p)为p值对应的s1；

c)令p＝p+1，若p≤l，则返回执行步骤b)，否则执行步骤d)；

d)若s1(q)不等于0，则在s2找到第一个非零元素的位置索引值p2，令s1(q)＝s2(p2)，s2(p2)＝0，其中s1(q)为q值对应的s1；

e)令q＝q+1，若q≤l，则执行步骤d)，否则结束；

3)进行α更新

在萤火虫算法中，α为步长因子，其作用是帮助萤火虫个体在其周围进行小范围的随机扰动，在对萤火虫个体进行β更新后，对更新后的个体的任务分配部分采用随机扰动的α更新，其目的是使得算法具有一定的局部随机搜索能力，α为步长因子，其公式为：

tai＝int(tai+α(rand-1/2))(5)

式(5)中，tai表示萤火虫任务分配部分某个元素的值，int是对参数取整操作，rand为随机因子；

4)在α更新后，萤火虫个体的任务分配部分出现非法解，因为任务分配部分的每个位都代表一个固定的任务，而每个任务都关联着可选无人机集合u^jh(以编号表示)，α更新可能会使得某些元素的取值超出该集合，所以有必要对更新后的编码进行非法修正，为避免使得算法过于复杂，尽量简化修正操作。

对α更新后的编码进行非法修正，非法修正即为对每一位元素进行可行性判断：若元素的值在元素的取值范围内，则不用修正，若元素的值超出取值范围，则以距离边界值最近的点代替元素值；

步骤5：萤火虫个体重构

1)对于萤火虫个体的ts部分，采用基于邻域搜索的变异方法，其操作步骤如下：

step1：在个体的任务排序部分随机选择r个位，并生成其排序的所有邻域；

step2：计算所有邻域的目标函数，选出目标函数值最高的个体作为最佳个体，并代替原来的个体；

2)交叉操作

为了提高种群的多样性，通过变异操作产生变异个体后需要进行交叉操作，而为了能够更好地平衡差分算子的全局搜索能力与局部搜索能力，采用随迭代次数指数递增的交叉概率因子：

采用随迭代次数指数递增的交叉概率因子：

cr＝crmin+(crmax-crmin)×exp(-a×(1-t/t)^b)(6)

式(6)中，cr为交叉概率因子，crmin和crmax分别为最小交叉率和最大交叉率，且crmin＝0.4，crmax＝0.6；a＝40，b＝4，t为设定的最大迭代次数，t为当前迭代次数，交叉操作得到的新个体的取值为：

其中，为交叉操作得到的新个体，是需要交叉操作的个体，为不需要进行交叉操作的个体，jrand为随机数；

3)选择操作

为了保持后代种群数量的恒定，也为了进化朝着更优的方向进行，算法的下一步采用贪婪策略进行选择，在原始个体和经交叉操作后得到的新个体之间选择目标函数值大的个体保留到下一代，选择操作为：

其中，x^ti是第t代的第i个个体，u^ti是第t代经交叉后得到的个体，fitness为目标函数；

步骤6：特殊耦合约束的处理

特殊耦合约束分为任务同时执行约束和任务优先级约束两种，虽然对于特殊耦合约束是针对目标而言，但是将其细化到每个子任务之间，用矩阵t^s∈r^3n×3n表示目标或任务间存在的特殊耦合约束关系，表示任务i与任务j的特殊耦合约束，其取值规则为：

步骤7：萤火虫个体解码与目标函数的计算

具体的解码步骤如下：

step1：对任务分配部分进行解码

(1)初始化各无人机的任务集合为空集，即

(2)从左至右依次读取萤火虫个体第k位上的值i，k＝1,2,…,2n，通过j＝fix(i/2)+1和h＝mod(i/2)分别得到j和h的值，将taskjh加入到tasksequencei中；

step2：对任务排序部分进行解码

(1)从左至右依次读取萤火虫个体第k位上的值j，k＝1,2,…,2n，每个j为目标tj上的一个任务，若j是第h次出现，则表示taskjh，当k＝2n得到所有任务的排列顺序tasks；

(2)将tasksequencei根据tasks重新排列任务顺序，当taskjh和taskkl均在tasksequencei中时，则以从左到右的顺序，若taskjh在tasks中的位置在taskkl前面，则yijhkl＝1，若taskjh在tasks中的位置在taskkl后面，则yijhkl＝-1；否则yijhkl＝0；

至此，解码结束，得到各无人机的任务执行序列tasksequencei。

在对个体解码后，可以得到每架无人机的任务执行序列tasksequencei，由于采用的目标函数为对最大航程的最小化，为了满足时间耦合约束，无人机有可能会因等待时机而在目标上空处于盘旋状态，盘旋过程中，无人机虽然不执行任何任务却仍要消耗燃油，因而在计算航程时仅仅计算目标与无人机之间的距离是不够的。无人机在执行任务过程中的速度vi保持固定，因此，以“航程＝飞行速度*飞行时间”计算无人机的航程，飞行时间为无人机开始执行任务到完成最后一个任务的时间段，考虑到无人机最终需要返回预先设置的基地，在航程后加上无人机最后一个任务到基地的距离作为最终的无人机航程。

为了满足特殊耦合约束，对萤火虫个体进行解码后计算目标函数时，对每架无人机的任务序列中的任务按照公式(9)判断与其存在特殊耦合约束的任务的分配情况；

由于无人机在同一时刻只能执行一个任务，即不能将具有任务同时执行约束的多个任务添加到同一架无人机的任务序列中，而对于设计的萤火虫个体来说很难完全避免，即使在初始化编码中添加避免逻辑，还是很难保证在个体更新中完全避免，鉴于此，从目标函数的角度出发，从算法寻优的角度去避免，当对萤火虫个体计算目标函数值时，若发现某无人机的任务序列中包含具有任务同时执行约束的任务，则令该萤火虫个体的适应度函数值为极差值。

本发明的实施例中，仿真环境为：intel2.53ghz主频，2g内存的pc机，windows7操作系统，matlab2014a平台。

我方有7架无人机，敌方有10个待摧毁目标，每个目标需要执行目标确认、打击和效果评估三类任务，三类任务间具有时间强耦合性，无人机配置及初始位置信息如表1所示，目标位置及着陆基地位置信息如表2所示，任务初始时刻t＝0。

表1

表2

整个战场的态势如图2所示，为方便表示，将所有任务进行编号，对于目标taskjh的编号no表示为：

no＝(j-1)*3+h

表3为无人机与任务的执行时间表，表中inf表示无穷大，即该无人机不能执行该任务。

表3

表3(续)

表3(续)

在战术考虑下，具有以下的特殊耦合约束：

(1)目标1和目标8需要同时被确认；

(2)目标4和目标10需要同时被打击；

(3)目标6需要在目标5被确认之前进行毁伤评估。

鉴于对任务同时执行约束的定义，令inter＝0.5h，即当两个任务被执行的时间间隔不超过0.5h，则满足任务同时执行约束，以上特殊耦合约束表示为：

式中，和分别表示目标1、目标8、目标4、目标10和目标5的确认开始时刻，表示目标6的毁伤评估结束时刻；

仿真结果与分析：

采用提出的de-dfa算法进行求解，具体的参数配置为：种群规模n＝50，最大迭代次数为100次，β0＝1，α＝0.5，ωg＝0.4，其中β0是初始吸引力，α是随机参数，ωg为变异概率，个体变异时的邻域范围为5，求得的最优分配方案以及各无人机的任务序列如表4所示，目标的被执行时刻如表5所示，本发明的迭代收敛过程如图3所示。

表4

表5

由表5可以看出，目标1和目标8分别在t＝6.25h和t＝6.7315h时被无人机2和无人机3确认，满足目标1和目标8同时被确认的特殊耦合约束，目标4和目标10分别在t＝25.3784h和t＝25.2045时被无人机6和无人机5打击，满足二者被同时打击的特殊耦合约束；目标6在t＝21.9453h时被无人机4执行毁伤评估任务，目标5在t＝24.1786h时被无人机4确认，满足目标6在目标5被确认之前被毁伤评估的任务优先级约束。此外，根据表4和表5的结果可以看出，任务分配结果同样满足时间耦合约束及其他约束，结果表明，本发明提出的de-dfa算法能够有效地解决同时存在特殊耦合约束和时间耦合约束的多无人机协同任务分配问题。

图4为本发明的任务分配甘特图，图5为本发明无人机执行任务过程的路径规划图，其中图5(a)为无人机1和无人机5执行任务时的路径规划图，图5(b)为无人机2和无人机4执行任务时的路径规划图，图5(c)为无人机3和无人机7执行任务时的路径规划图，图5(d)为无人机6执行任务时的路径规划图。