近空间可变翼飞行器自适应小翼切换控制系统及工作方法与流程

本发明属于航空航宇推进控制技术领域，具体指代一种近空间可变翼飞行器自适应小翼切换控制系统及工作方法。

背景技术：

近空间飞行器所采用的推进动力是无需自带氧化剂的超声速燃烧冲压式发动机，气动布局为机体/发动机一体化设计。近空间飞行器的弹性机体与飞行推进系统之间存在很强的耦合性，飞行器模型的非线性特性十分严重，飞行过程具有快速时变性，近空间飞行器的气动特性变化剧烈，各种不确定性严重，传统的经典控制方法无法很好地满足飞行控制系统稳定性和强鲁棒性的性能要求。因此要保证飞行控制系统的实时性，鲁棒性和稳定性，对响应速度和控制精度提出了更高的要求，这极大地推动了先进的控制方法和控制理论关键技术的发展。

近空间可变翼飞行器是具有可伸缩小翼的近空间飞行器，是为了解决起飞爬升段升力不足、升阻比过小，满足飞行速度和飞行高度包络范围大的特点而设计的一种可变翼飞行器。近空间可变翼飞行器兼具近空间飞行器与可变翼飞行器的特点，可以用于高空高速飞行，可变翼的特点可以使飞行器根据不同的飞行环境和飞行状态选择伸出或是收回小翼，一般在低速飞行时伸出小翼，提高升力，在高速飞行时，收回小翼以减小阻力，减小燃油消耗。

近空间可变翼飞行器所处的飞行环境、自身复杂多变的气动特性对飞行控制系统的设计带来了很多技术上的难点。第一，飞行控制系统必须满足稳定性要求。大跨度飞行包络，严重的外界干扰，弹性形变、高温和低密度流效应等因素会严重影响系统的稳定性。第二，飞行控制系统必须满足鲁棒性要求。在高动压、高速环境下，各种外界干扰和内部参数变化要求飞行控制系统必须具有较强的鲁棒性。飞行器的所处大气环境复杂，使得飞行器异常敏感，时变性强，很容易产生基础结构失真和参数不确定性；第三，强耦合和非线性特点要求系统的协调控制。近空间可变翼飞行器多采用乘波体或升力体气动布局以保证机动飞行的大迎角姿态，采用机体/发动机一体化设计可以保证高速飞行时不解体。第四，实时性要求。在高速飞行时，飞行参数具有激烈快时变的特征，而气动舵面的控制效果反而锐减，系统反应时间加长，会出现控制延时问题。在控制器设计时要充分考虑机翼变形的实时性，控制算法的复杂度，要避免控制参数过多，提高算法的运行速度。第五，要满足约束条件。飞行控制系统在保证控制精度的同时，还要满足一些约束条件，例如执行机构的饱和约束、迎角和侧滑角约束，在爬升和再入返回段的热流约束、为保证机体结构强度而设置的动压约束和过载约束等。

滑模控制方法通过设计不连续的控制器，迫使系统产生滑动运动模态，一旦系统进行滑动模态，系统将对不确定性和干扰具有完全不变性。然而，实际系统由于切换装置不可避免地存在惯性，变结构系统在不同的控制逻辑中来回切换将导致实际滑动模态不是准确地发生在切换面上，容易引起系统的剧烈抖动，不能保证系统的鲁棒性。

增益预置控制方法在控制系统设计中的应用比较成熟并取得了一定的成果，当非线性系统变化范围较大时，采用这种方法需要设计多个平衡点，整个控制器的稳定性难以得到保证。在高超声速飞行器大迎角和高机动状态下，飞行状态呈现强非线性和高耦合性，增益预置方法无法满足性能指标的要求。

动态逆控制方法通过被控对象非线性耦合特性的准确建模，在线构成非线性耦合时变控制器，以抵消对象的非线性耦合时变特性，使系统成为伪线性系统。但是动态逆方法对建模误差敏感，且通常情况下，非线性系统精确建模非常困难，一旦建模与实际系统有差别，非线性耦合特性的对消就会有影响，导致控制性能的恶化，不能保证鲁棒性。

技术实现要素：

针对于上述现有技术的不足，本发明的目的在于提供一种可变翼高超声速飞行器自适应控制系统及工作方法，可有效解决近空间可变翼飞行器在小翼伸出与收回切换过程中的不确定性的飞行控制问题。

为达到上述目的，本发明的一种可变翼高超声速飞行器自适应控制系统，其用于生成近空间可变翼飞行器的控制输入量u(t)，以保证近空间可变翼飞行器飞行速度v、飞行俯仰角θ能快速跟踪到输入的飞行速度参考值vr、飞行俯仰角参考值θr；该控制系统包括：参考模型、标称控制器和自适应更新模块；其中，

参考模型，根据模型阶次，设计一阶、二阶参考模型：

式中，δym(t)＝[δvm,δθm]^t为参考模型输出，δr(t)为参考模型输入，wm(s)为参考模型的传递函数，为关联矩阵，p1,p2,p3为配置的稳定极点；

标称控制器，其形式如下：

其中，是标称控制器参数，

为高频增益矩阵；

标称控制器的作用下得到飞行器的输出δy(t)＝g(s)δu(t)，此时的输出δy(t)能跟踪上述参考模型输出δym(t)；

自适应更新模块，其形式如下：

式中，k2为自适应更新参数，其为标称控制器参数的趋近律，k2选取的值为更新初值，自适应更新函数表达式如下：

误差更新函数为：

其中，定义一些辅助变量：

为估计误差，

为自适应更新函数中间变量，

为误差更新函数中间变量，

为归一化函数，

ω(t)＝[δv,δγ,δα,δq,δθ,δvc,δθc]^t为新的状态量函数，

sp∈r^m×m,为自适应增益矩阵；

自适应更新模块自动更新控制量δu(t)，得到飞行器的输出δy(t)＝g(s)δu(t)，此时的输出δy(t)能精确跟踪参考模型输出δym(t)。

优选地，所述的参考模型的传递函数

为一阶和二阶环节组成，p1,p2,p3为配置的稳定极点；速度的相对阶次是一阶，所以选择一阶惯性环节；俯仰角的相对阶次是二阶，所以选择二阶惯性环节。

优选地，所述的标称控制器和自适应更新模块的参数：

其中，δδe(t)为升降舵增量，δβc(t)为油门百分比增量，δv(t)为速度增量，δγ(t)为航迹角增量，δα(t)为迎角增量，δq(t)为俯仰角速率增量，δθ(t)为俯仰角增量，δvc(t)为速度指令信号，δθc(t)为俯仰角指令信号，βc为可变翼高超声速飞行器的发动机节流阀调定值，δe为可变翼高超声速飞行器的升降舵偏转值。

优选地，所述的近空间可变翼飞行器的控制输入量u(t)＝δu(t)+u^*，其中(x^*,u^*)为线性化的平衡点。

本发明的一种可变翼高超声速飞行器自适应控制系统的工作方法，包括步骤如下：

1)将近空间飞行器非线性模型线性化得到状态方程表达式如下：

δy＝cδx

式中，δu(t)＝[δδe(t)，δηe(t)]^t，δy(t)＝[δv(t)，δθ(t)]^t，

δx(t)＝[δv(t)，δγ(t)，δα(t)，δq(t)，δθ(t)]^t；

2)根据速度与俯仰角的相对阶次，选择参考模型如下：

δym(t)＝diag[1/(s+p1),1/(s+p2)(s+p3)]δr(t)

选择速度与俯仰角指令作为参考模型输入δr(t)＝[δvc,δθc]^t，得到参考模型输出δym(t)＝[δvm,δθm]^t；

3)将标称控制器输出加上线性化平衡状态值u^*，即u＝δu+u^*输入到飞行器非线性模型，得到飞行器输出δy(t)，使其跟踪δym(t)；

4)在标称控制器作为初始输入基础之上加入自适应更新模块，得到自适应控制律即将u＝δu+u^*输入到飞行器非线性模型；飞行器的小翼在25秒之后缓慢伸出，30秒时完全伸出，自适应更新模块在小翼伸出时更新参数，保证对速度与俯仰角的稳定跟踪。

本发明的有益效果：

1、本发明具有良好的全局稳定性，能有效利用基于状态方程设计控制器不依赖于非线性系统本身的特性，基于该方法设计出的控制系统在处理近空间飞行器问题时拥有更大的灵活性，可有效地保证其全局稳定性。

2、当控制系统小翼由收缩到伸出或由伸出到收缩的情况下，自适应更新律能有效抵消参数不确定对系统的影响，使得近空间可变翼飞行器能快速有效的响应跟踪信号，具有较好的跟踪性能和鲁棒性能。

3、所设计的自适应控制器的自适应更新律是实时、动态更新的过程，可以提高系统的实时性。

附图说明

图1为本发明控制系统的结构原理示意图；

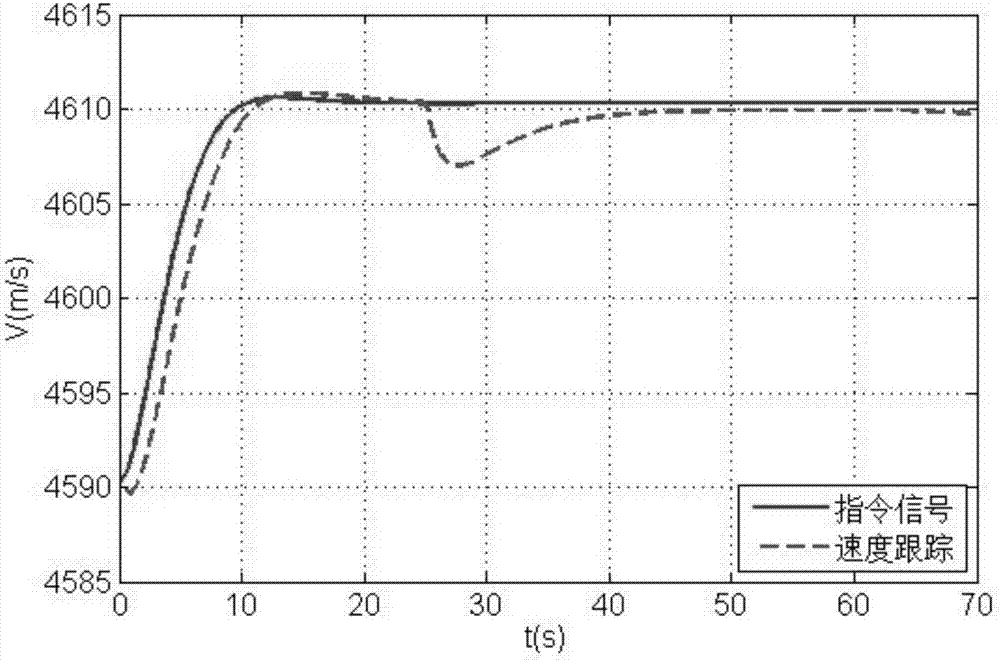
图2为本发明控制系统的速度跟踪响应曲线图；

图3为本发明控制系统的俯仰角跟踪响应曲线图。

具体实施方式

为了便于本领域技术人员的理解，下面结合实施例与附图对本发明作进一步的说明，实施方式提及的内容并非对本发明的限定。

本发明基于状态反馈输出跟踪的模型参考自适应控制系统设计方法是将建立的参考模型作为控制器设计的基础，因此它不依赖与飞行器的非线性模型，在实际应用中较为简单，控制器分为标称控制器和自适应更新律，根据状态方程设计标称控制器参数，并将标称控制器参数作为自适应更新律的初值，并借助李亚普诺夫函数设计自适应更新律，以保证系统的全局稳定性。该方法适用于线性控制，不依赖于数学模型，具有非常独特的优势，可以提高控制系统的稳定性和鲁棒性能。

参照图1所示，本发明的一种可变翼高超声速飞行器自适应控制系统，其应用于可变翼高超声速飞行器中，该可变翼高超声速飞行器的输入输出形式：y(t)＝g(s)u(t)，增量形式为δy(t)＝g(s)δu(t)，状态方程表达式为：δy(t)＝cδx(t)，其中g(s)为飞行器传递函数，y(t)为飞行器的输出，u(t)为飞行器的控制输入，x(t)为飞行器状态量，a,b,c为系统矩阵；该控制系统用于生成近空间可变翼飞行器的控制输入量u(t)，以保证近空间可变翼飞行器飞行速度v、飞行俯仰角θ能快速跟踪到输入的飞行速度参考值vr、飞行俯仰角参考值θr；该控制系统包括：参考模型、标称控制器和自适应更新模块；

以某型近空间可变翼飞行器为例，其采用翼身融合布局，机体轮廓为三角形，大后掠机翼与机身采用翼身融合方式，升降舵布置在机翼后缘，机翼为可变形翼面，采用在主翼两侧伸缩小翼的方式提高升力和飞行效率。该飞行器在高超声速巡航飞行条件下的纵向运动模型描述为：

式中，状态量v,γ,α,q,θ分别表示飞行器速度，飞行航迹倾斜角，飞行迎角，俯仰角速率和飞行俯仰角；l,d,t分别表示飞行器升力、阻力和发动机推力，m表示俯仰力矩，iyy表示纵向转动惯量，∫(x²+z²)dm＝iyy；

气动力和力矩表示为：

l＝0.5ρv²scl

d＝0.5ρv²scd

myy＝0.5ρv²sc[cm(α)+cm(δe)+cm(q)]

式中，ρ为大气密度，s为机翼浸润面积，cl，cd，cm分别为升力系数，阻力系数和俯仰力矩系数；

小翼伸缩模型如下：

式中，s为机翼面积，小翼在25s时刻开始伸出，伸出前机翼面积s＝369m/s，在30s时刻完成小翼的伸出，小翼完全伸出机翼面积s＝389m/s；小翼伸出过程中机翼面积变化影响飞行器升力系数cl、阻力系数cd和俯仰力矩系数cm发生变化。

将上述近空间可变翼飞行器非线性模型线性化得到状态方程表达式为：

标称控制器和自适应更新模块的设计目标是当小翼切换时出现不确定性扰动的情况下，使得近空间可变翼飞行器能稳定跟踪给定速度参考信号和俯仰角参考信号yr＝[vr(t)θr(t)]^t，t≥0。

在标称控制器和自适应更新模块设计之前，作如下假设：

假设1：g(s)＝c(si-a)^-1b的所有零点稳定，并且系统(a,b,c)可控且可观测。

假设2：g(s)严格有理，满秩，并且有一个对角关联矩阵

ξm(s)＝diag{d1(s),d2(s),…,dm(s)}

式中，为首一稳定多项式，也就是说高频增益矩阵定义为：

该矩阵有界，并且非奇异。

假设3：存在已知矩阵sp∈r^m×m满足

参考模型，根据模型阶次，设计一阶、二阶参考模型：

式中，δym(t)＝[δvm,δθm]^t为参考模型输出，δr(t)为参考模型输入，wm(s)为参考模型的传递函数，为关联矩阵，参考模型由一阶和二阶环节组成，p1,p2,p3为配置的稳定极点，速度的相对阶次是一阶，所以选择一阶惯性环节，俯仰角的相对阶次是二阶，所以选择二阶惯性环节。

标称控制器，其形式如下：

其中，是标称控制器参数，为高频增益矩阵；

标称控制器的作用下得到飞行器的输出δy(t)＝g(s)δu(t)，此时的输出δy(t)能跟踪上述参考模型输出δym(t)；

自适应更新模块，将标称控制器应用到系统中，得到闭环系统：

并且输出跟踪误差为：

式中，ω(t)＝[x^t(t),r^t(t)]^t,

为得到自适应更新模块的参数向量θ^t(t)的更新律，令ψ^*＝kp,h(s)＝1/(s+p2)(s+p3)，相对阶ρm的稳定多项式为1/(s+p2)(s+p3)，定义估计误差为：

ε(t)＝ξm(s)h(s)[δy-δym](t)+ψ(t)ξ(t)

式中，ψ(t)是ψ^*的估计误差，并且

ζ(t)＝h(s)[ω](t)

ξ(t)＝θ^t(t)ζ(t)-h(s)[δu](t)

估计误差还可以写成

式中，

选择以下自适应参数更新律

式中，γ＝γ^t＞0,且

得到自适应控制器如下：

式中，k2为标称控制参数的趋近律，且更新律为

定义跟踪误差e(t)＝δy(t)-δym(t)满足

证明：可以找到一个正定的方程：

其导数为：

根据李雅普诺夫稳定性定理可知，闭环系统信号有界且输出能够实现渐进跟踪参考模型。

为了验证本实例的效果，对其进行数值仿真验证。为了描述飞行器小翼伸缩的不确定性，仿真中小翼在25s时刻开始伸出，伸出前机翼面积s＝369m/s，在30s时刻完成小翼的伸出，小翼完全伸出机翼面积s＝389m/s。小翼伸出过程中机翼面积变化影响飞行器升力系数cl、阻力系数cd和俯仰力矩系数cm发生变化。利用本实例控制系统所得到的近空间可变翼飞行器高度和俯仰角的跟踪响应曲线如图2、3所示。

本发明的一种可变翼高超声速飞行器自适应控制系统的工作方法，包括步骤如下：

1)将近空间飞行器非线性模型线性化得到状态方程表达式如下：

δy＝cδx

式中，δu(t)＝[δδe(t)，δβc(t)]^t，δy(t)＝[δv(t)，δθ(t)]^t，

δx(t)＝[δv(t)，δγ(t)，δα(t)，δq(t)，δθ(t)]^t；

2)根据速度与俯仰角的相对阶次，选择参考模型如下：

δym(t)＝diag[1/(s+p1),1/(s+p2)(s+p3)]δr(t)

选择速度与俯仰角指令作为参考模型输入δr(t)＝[δvc,δθc]^t，得到参考模型输出δym(t)＝[δvm,δθm]^t；

3)将标称控制器输出加上线性化平衡状态值u^*，即u＝δu+u^*输入到飞行器非线性模型，得到飞行器输出δy(t)，使其跟踪δym(t)；

4)在标称控制器作为初始输入基础之上加入自适应更新模块，得到自适应控制律即将u＝δu+u^*输入到飞行器非线性模型；飞行器的小翼在25秒之后缓慢伸出，30秒时完全伸出，自适应更新模块在小翼伸出时更新参数，保证对速度与俯仰角的稳定跟踪。

本发明具体应用途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进，这些改进也应视为本发明的保护范围。