一种快速求解冗余度机械臂关节角偏移问题的方法与流程

本发明涉及冗余度机械臂控制领域，具体涉及一种基于变参收敛微分神经网络来解决冗余度机械臂关节角偏移问题的方法。

背景技术：

冗余度机械臂在完成末端执行任务时具有比其所需自由度更多的自由度，这种更多的自由度可以提高机械臂的性能，如躲避障碍物和奇异点等。但是更多的自由度就意味着对应一个末端执行器位置点，可以得到无穷个关节角度解。所以末端执行器在完成一个闭合路径任务时，冗余度机械臂的关节角偏移问题就很有可能会出现。如果关节角偏移问题不能得以解决，就会影响到下个周期任务的精度，甚至会使机械臂的关节扭伤，影响生产过程，损害周围设备并伤害工作人员。固然我们可以在每个周期任务完成时通过调节关节的运动来解决关节角偏移问题，但是这种方法效率很低。

一种传统的解决关节角偏移问题的方法是基于伪逆的方法，但是这种方法并不能在任何关节状态下都能解决问题。为了解决冗余度机械臂的关节角偏移问题，关节角无偏移规划被提出，其主要思想是最小化关节角的末状态和初状态的差，接着将关节角无偏移规划写成标准的二次规划问题，求解二次规划问题的方法有数值方法求解器和神经网络求解器，其中神经网络求解器在近年来更受欢迎。因为神经网络求解器具有并行计算能力和更好的效率。在目前的神经动力学方法中，设计参数都是固定的，而本发明的神经网络设计参数是随着时间变化的，具有更快的收敛速度，鲁棒性更好，又因为设计方法基于微分理论，称为变参收敛微分神经网络。

技术实现要素：

本发明的目的是针对现有技术的不足，提供了一种快速求解冗余度机械臂关节角偏移问题的方法。

本发明的目的可以通过如下技术方案实现：

一种快速求解冗余度机械臂关节角偏移问题的方法，所述方法包括以下步骤：

1)将冗余度机械臂关节角速度层的逆运动学问题设计为考虑反馈的关节角无偏移规划；

2)将步骤1)的关节角无偏移规划写成一个标准的二次规划；

3)将步骤2)中标准的二次规划通过拉格朗日乘子法转化为时变矩阵等式的求解问题；

4)将步骤3)的时变矩阵等式用变参收敛微分神经网络来求解。

进一步地，所述步骤1)的将冗余度机械臂关节角速度层的逆运动学问题设计为考虑反馈的关节角无偏移规划，即将冗余度机械臂关节角速度层无偏移性能指标设计为最小化，受约束于其中，θ(t)表示关节角度矢量，表示关节角速度矢量，w(t)表示i为单位矩阵，r(t)表示机械臂末端执行器位置矢量，表示机械臂末端执行器位置速度矢量，j(θ)表示雅可比矩阵c(t)为k(θ(t)-θ(0))，k为用来控制关节偏移的收敛系数，上标t表示转置，在约束等式中，为机械臂关节角速度层的逆运动学方程，k(r(t)-f(θ))表示添加反馈控制，k表示正定对称的反馈增益矩阵，f(·)表示机械臂末端执行器位置矢量关于关节角度矢量的非线性关系。

进一步地，所述步骤2)的将关节角无偏移规划写成一个标准的二次规划，即设计性能指标为最小化(x^t(t)w(t)x(t))/2+c^t(t)x(t)，受约束于j(θ)x(t)＝b(t)，其中c(t)＝k(θ(t)-θ(0))，

进一步地，所述步骤3)将标准的二次规划通过拉格朗日乘子法l(x(t),λ(t),t)＝(x^t(t)w(t)x(t))/2+c^t(t)x(t)+λ^t(t)(j(θ)x(t)-b(t))转化为时变矩阵等式a(t)y(t)＝g(t)的求解问题，其中λ(t)为拉格朗日因子，

进一步地，所述步骤4)将时变矩阵等式用变参收敛微分神经网络来求解，即其中(γ+t^γ)为变参收敛微分神经网络的收敛速度参数，φ(·)为激活函数矢量，由确定数量的标量单调递增的奇的激活函数子函数φ(·)组成。

本发明与现有技术相比，具有如下优点和有益效果：

1、本发明通过微分方程理论，设计了带有变参的负的时间倒数的神经网络，具有超指数收敛性，使收敛速度大大增加。

2、本发明采用带有变参的负的时间倒数的神经网络来求解关节角无偏移规划，大幅提高了关节角无偏移精度，大幅减小了关节角偏移值。

附图说明

图1为本发明实施例快速求解冗余度机械臂关节角偏移问题方法的流程图。

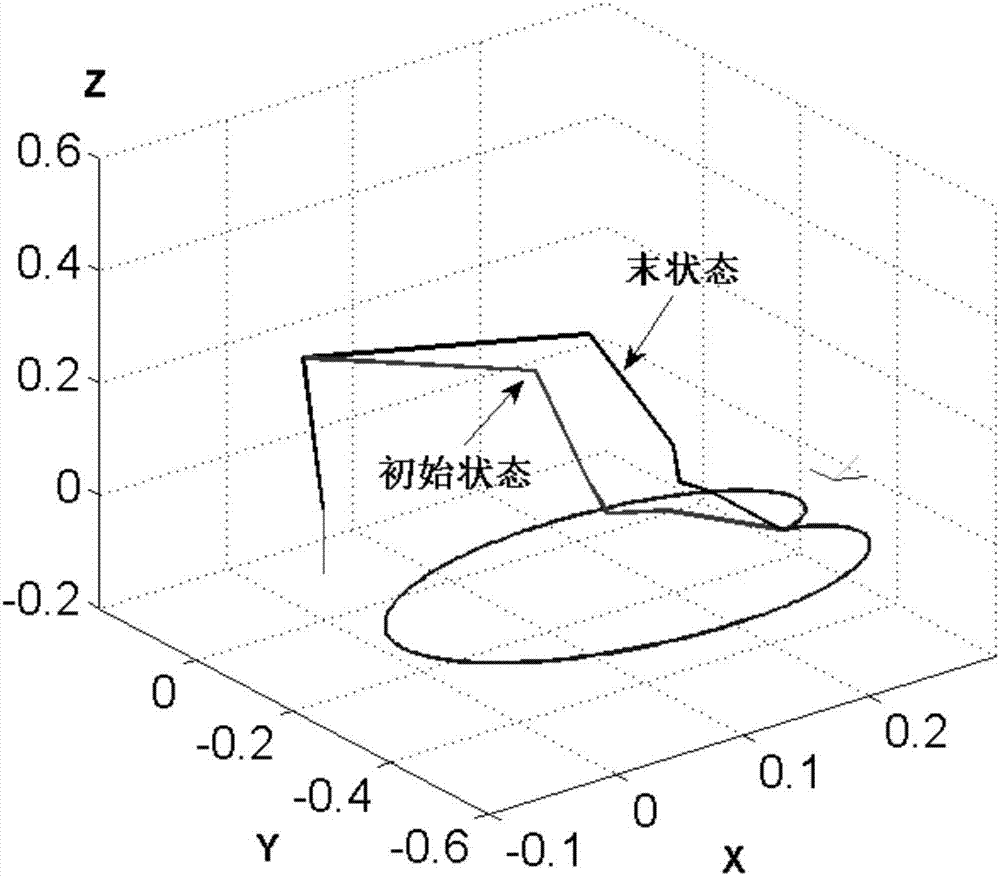
图2为冗余度机械臂出现关节角偏移问题的示意图。

图3为实现了本发明实施例的冗余度机械臂关节角无偏移规划的示意图。

具体实施方式

下面结合实施例及附图对本发明作进一步详细的描述，但本发明的实施方式不限于此。

实施例：

本实施例提供了一种快速求解冗余度机械臂关节角偏移问题的方法，流程图如图1所示，包括以下步骤：

1)将冗余度机械臂关节角速度层的逆运动学问题设计为考虑反馈的关节角无偏移规划；

2)将步骤1)的关节角无偏移规划写成一个标准的二次规划；

3)将步骤2)中标准的二次规划通过拉格朗日乘子法转化为时变矩阵等式的求解问题；

4)将步骤3)的时变矩阵等式用变参收敛微分神经网络来求解。

图2为机械臂出现关节角偏移问题的示意图，给定末端任务为一个闭合的桃心形曲线，由图中可看出，当机械臂完成闭合路径的任务后，机械臂的末状态和初始状态不重合，出现了关节角偏移问题。经过本实施例的改进后，实现了机械臂关节角的无偏移规划，示意图如图3所示。

所述方法的具体过程如下：将冗余度机械臂关节角速度层的逆运动学问题设计为考虑反馈的关节角无偏移规划，即将冗余度机械臂关节角速度层无偏移性能指标设计为最小化，受约束于其中，θ(t)表示t时刻的关节角度矢量，表示t时刻的关节角速度矢量，w(t)表示θ(0)表示关节角度的初始状态，为(θ(t)-θ(0))的二范数的平方，i为单位矩阵，r(t)表示机械臂末端执行器位置矢量，r(t)表示机械臂末端执行器位置速度矢量，j(θ)表示雅可比矩阵c(t)为k(θ(t)-θ(0))，k用来控制关节偏移的收敛系数，上标t表示转置，在约束等式中，为机械臂关节角速度层的逆运动学方程，k(r(t)-f(θ))表示添加反馈控制，k表示正定对称的反馈增益矩阵，f(·)表示机械臂末端执行器位置矢量关于关节角度矢量的非线性关系；

将上述关节角无偏移规划写成一个标准的二次规划，即设计性能指标为最小化(x^t(t)w(t)x(t))/2+c^t(t)x(t)，受约束于j(θ)x(t)＝b(t)，其中c(t)＝k(θ(t)-θ(0))，

通过拉格朗日乘子法构造拉格朗日函数：

l(x(t),λ(t),t)＝(x^t(t)w(t)x(t))/2+c^t(t)x(t)+λ^t(t)(j(θ)x(t)-b(t))

其中λ(t)为拉格朗日因子，拉格朗日函数分别对x(t)和λ(t)求偏导并令其等于零得：

写为一个时变矩阵等式：a(t)y(t)＝g(t)，其中：

定义矢量误差函数：ε(t)＝a(t)y(t)-g(t)，为了让矢量误差函数趋近于零，根据神经动力学的设计方法，需要矢量误差函数有负的时间倒数，则可以设计如下负的时间倒数：(dε(t))/dt＝-(γ+t^γ)φ(ε(t))，其中：(γ+t^γ)为变参收敛微分神经网络的收敛速度参数，φ(·)为激活函数矢量，由确定数量的标量的单调递增的奇的激活函数子函数φ(·)组成，将矢量误差函数代入设计的负的时间导数得到如下隐式动力学方程：由于此种设计方法是基于微分方程理论，并且设计参数(γ+t^γ)是随时间变化的，所以称为变参收敛微分神经网络。

以上所述，仅为本发明专利较佳的实施例，但本发明专利的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明专利所公开的范围内，根据本发明专利的技术方案及其发明专利构思加以等同替换或改变，都属于本发明专利的保护范围。