一种四旋翼无人机系统的增强型双幂次趋近律滑模控制方法与流程
本发明涉及一种四旋翼无人机系统的增强型双幂次趋近律滑模控制方法。
背景技术:
四旋翼飞行器作为旋翼式飞行器的一种,以其体积小、机动性能好、设计简单、制造成本低廉等优点,吸引了国内外大学、研究机构、公司的广泛关注。旋翼无人飞行器非常适合用于监视、侦察等民用和军用领域。在民用领域,旋翼无人飞行器主要被应用于抗灾救险、地面监测、高空航拍等;由于其隐蔽性髙,可靠性好,也被用于战场监控、军事侦察等军用领域。在科研方面,四旋翼无人机具有非线性、欠驱动、强耦合的动态特性,研究人员常将其作为理论研究、方法验证的实验载体。针对四旋翼无人机系统的控制问题,存在很多控制方法,例如pid控制,自适应控制,滑模控制等。
趋近律滑模控制的方法可以提高四旋翼无人机快速性,鲁棒性,而且大大减弱了传统滑模控制带来的抖振问题。由于滑模可以按需要来设计,而且系统的滑模运动与控制对象的参数变化和外界的干扰无关,因此滑模变结构控制系统的鲁棒性比一般常规的连续系统强。但是,传统的滑模变结构会造成奇异性问题和抖振现象。对比传统的双幂次趋近律滑模控制,增强型双幂次趋近律滑模趋近速度可以做到自我调整,趋近速度更快,到达时间更短而且不增加抖振现象。
技术实现要素:
为了克服现有的四旋翼无人机系统存在的趋近速度过慢、抖振剧烈、到达时间过长的不足,本发明提供一种四旋翼无人机系统的增强型双幂次趋近律滑模控制方法,保证系统更快地到达滑模面。
为了解决上述技术问题提出的技术方案如下:
一种四旋翼无人机系统的增强型双幂次趋近律滑模控制方法,包括以下步骤:
步骤1,确定从基于四旋翼无人机的机体坐标系到基于地球的惯性坐标系的转移矩阵;
其中ψ、θ、φ分别是无人机的偏航角、俯仰角、翻滚角,表示无人机绕依次惯性坐标系各轴旋转的角度,tψ表示ψ的转移矩阵,tθ表示θ的转移矩阵,tφ表示φ的转移矩阵;
步骤2,根据牛顿欧拉公式分析无人机动力学模型,过程如下:
2.1,平动过程中有:
其中x、y、z分别表示无人机在惯性坐标系下的位置,m表示无人机的质量,g表示重力加速度,mg表示无人机所受重力,四个旋翼产生的合力ur;
2.2,转动过程中有:
其中τx、τy、τz分别代表机体坐标系上的各轴力矩分量,ixx、iyy、izz分别代表机体坐标系上的各轴转动惯量分量,×表示叉乘,wp、wq、wr分别代表机体坐标系上的各轴姿态角速度分量,
考虑到无人机一般处于低速飞行或者悬停状态下,姿态角变化较小,认为
联立式(1),(2),(4),得到无人机的动力学模型如式(5)所示
其中
2.3,根据式(5),对位置姿态关系进行解耦计算,结果如下:
其中φd为φ的期望信号值,θd为θ的期望信号值,ψd为ψ的期望信号值,arcsin函数是反正弦函数,arctan函数是反正切函数;
步骤3,在每一个采样时刻,计算位置的跟踪误差、位置滑模面及其一阶导数,根据式(6)解耦出合外力ur和姿态角的期望值φd、θd、计算姿态角的跟踪误差、姿态角的滑模面及其一阶导数,设计出位置控制器和姿态角控制器,过程如下:
3.1,定义位置跟踪误差及其一阶微分和二阶微分:
其中i=1、2、3,x1=x,x2=y,x3=z,x1d表示x的期望信号,x2d表示y的期望信号,x3d表示z的期望信号,e1表示x的位置跟踪误差,e2表示y的位置跟踪误差,e3表示z的位置跟踪误差;
3.2,定义位置的滑模面:
其中ci为正常数,s1为x的滑模面,s2为y的滑模面,s3为z的滑模面;
3.3,分别对式(8)两边进行求导,得滑模面的一阶导数为
把式(7)代入式(9),得到
把式(5)代入式(10),得到
其中u1=ux,u2=uy,u3=uz;
3.4,选择趋近律滑模
其中
联立式(10)、式(11),得到位置控制器的输入:
3.5,根据式(6)解耦出合外力ur,和姿态角的期望值φd、θd,定义姿态角的跟踪误差及其一阶微分和二阶微分:
其中j=4、5、6,x4=φ,x5=θ,x6=ψ,x4d表示φ的期望信号,x5d表示θ的期望信号,x6d表示ψ的期望信号,e4表示φ的跟踪误差,e5表示θ的跟踪误差,e6表示ψ的跟踪误差;
3.6,定义姿态角的滑模面:
其中cj为正常数,s4为φ的滑模面,s5为θ的滑模面,s6为ψ的滑模面;
3.7,分别对式(14)两边进行求导,得姿态角的滑模面的一阶导数为
把式(13)代入式(15),得到
把式(5)代入式(16),得到
其中uj为姿态角控制器的输入,u4=τx,u5=τy,u6=τz,
3.8,选择趋近律滑模
其中
联立式(17)、式(18),得到姿态角控制器的输入:
进一步,所述增强型双幂次趋近律滑模控制方法还包括以下步骤:
步骤4,证明滑动模态可以在有限时间到达平衡零点附近,同时验证增强型双幂次趋近律的到达时间小于传统双幂次趋近律的到达时间,过程如下;
4.1,设计李雅普诺夫函数
其中
由于d(s)>0,则
4.2与传统双幂次趋近律滑模控制方法比较到达时间,过程如下:
对于增强型双幂次趋近律,当初始位置s(0)>1时,对于s(0)→s=1的过程中,第一项起主导作用,因此有式(19)
当初始位置s(0)<-1时,对于s(0)→s=-1的过程中,第一项起主导作用
联立(20),(21)对于s(0)→sign[s(0)]的过程中,得(22)
其中|s(0)|>1;
对于传统双幂次趋近律,s(0)→sign[s(0)]的过程中的到达时间为
因此,在s(0)→sign[s(0)]的过程中,增强型双幂次趋近律的到达时间比传统双幂次趋近律的到达时间更短;
同理,在sign[s(0)]→0的过程中,第二项起主导作用
增强型双幂次的到达时间为
传统双幂次趋近律的到达时间为
因此,在sign[s(0)]→0的过程中,增强型双幂次趋近律的到达时间比传统双幂次趋近律的到达时间更短;
综上所述,增强型双幂次趋近律的到达时间比传统双幂次趋近律的到达时间更短。
本发明基于增强型双幂次趋近律控制,设计机四旋翼无人机系统的滑模控制方法,实现系统稳定控制,减短滑动模态到达滑模面的时间以此来缩短无人机定点飞行所需的时间。
本发明的技术构思为:针对四旋翼无人机系统,结合双幂次趋近律滑模控制方法,设计一种四旋翼无人系统的增强型双幂次趋近律滑模控制方法。增强型双幂次趋近律的设计是为了保证系统的滑动模态能更快的到达滑模面,同时不增加系统的抖振现象,实现系统的快速稳定控制。
本发明的优点为:增强了系统的鲁棒性,与传统的双幂次趋近律滑模控制相比,在不增加抖振的情况下,缩短了滑动模态的到达时间,从而使系统更快地实现稳定收敛。
附图说明
图1为四旋翼无人机的位置跟踪效果示意图,其中虚线代表传统双幂次趋近律控制,点线代表增强型双幂次趋近律控制。
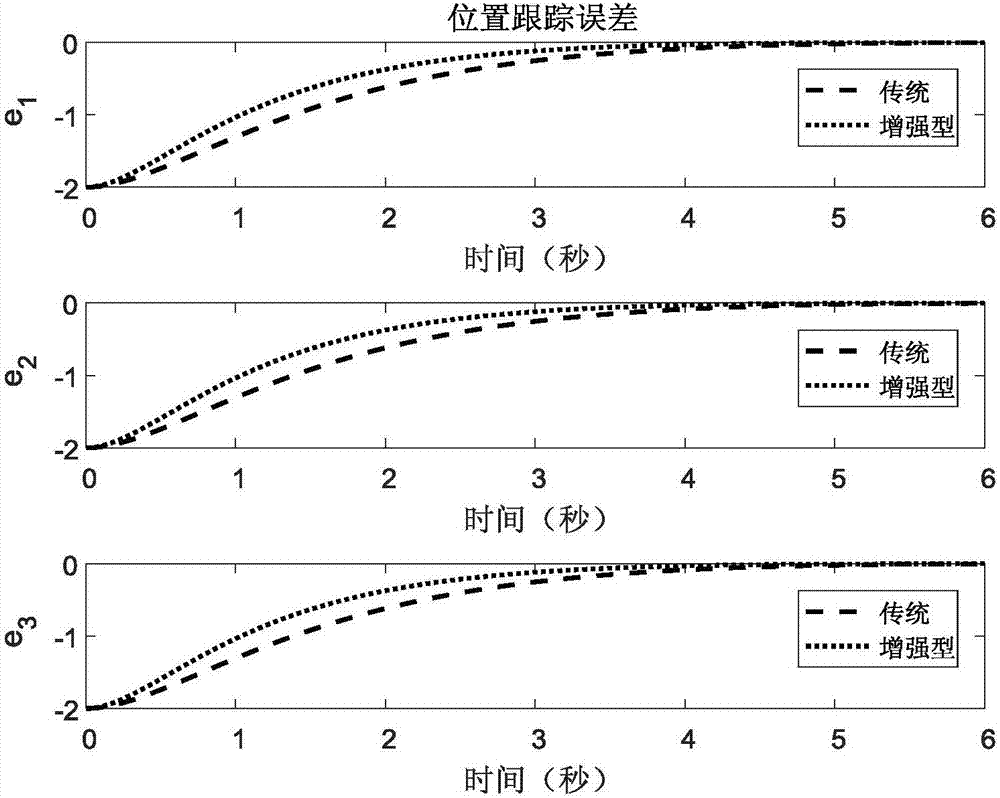
图2为四旋翼无人机的位置跟踪误差示意图,其中虚线代表传统双幂次趋近律控制,点线代表增强型双幂次趋近律控制。
图3为四旋翼无人机的传统双幂次趋近律控制下的位置控制器输入示意图。
图4为四旋翼无人机的增强型双幂次趋近律控制下的位置控制器输入示意图。
图5为四旋翼无人机的传统双幂次趋近律控制下的姿态角控制器输入示意图。
图6为四旋翼无人机的增强型双幂次趋近律控制下的姿态角控制器输入示意图。
图7为位置滑模面的示意图,其中虚线代表传统双幂次趋近律控制,点线代表增强型双幂次趋近律控制。
图8为位置滑模面的示意图,其中虚线代表传统双幂次趋近律控制,点线代表增强型双幂次趋近律控制。
图9为本发明的控制流程示意图。
具体实施方式
下面结合附图对本发明做进一步说明。
参照图1-图9,一种四旋翼无人机系统的增强型双幂次趋近律滑模控制方法,包括以下步骤:
步骤1,确定从基于四旋翼无人机的机体坐标系到基于地球的惯性坐标系的转移矩阵;
其中ψ、θ、φ分别是无人机的偏航角、俯仰角、翻滚角,表示无人机绕依次惯性坐标系各轴旋转的角度,tψ表示ψ的转移矩阵,tθ表示θ的转移矩阵,tφ表示φ的转移矩阵;
步骤2,根据牛顿欧拉公式分析无人机动力学模型;
2.1,平动过程中有:
其中x、y、z分别表示无人机在惯性坐标系下的位置,m表示无人机的质量,g表示重力加速度,mg表示无人机所受重力,四个旋翼产生的合力ur;
2.2,转动过程中有:
其中τx、τy、τz分别代表机体坐标系上的各轴力矩分量,ixx、iyy、izz分别代表机体坐标系上的各轴转动惯量分量,×表示叉乘,wp、wq、wr分别代表机体坐标系上的各轴姿态角速度分量,
考虑到无人机一般处于低速飞行或者悬停状态下,姿态角变化较小,认为
联立式(1),(2),(4),得到无人机的动力学模型如式(5)所示
其中
2.3,根据式(5),对位置姿态关系进行解耦计算,结果如下:
其中φd为φ的期望信号值,θd为θ的期望信号值,ψd为ψ的期望信号值,arcsin函数是反正弦函数,arctan函数是反正切函数;
步骤3,在每一个采样时刻,计算位置的跟踪误差、位置滑模面及其一阶导数,根据式(6)解耦出合外力ur和姿态角的期望值φd、θd、计算姿态角的跟踪误差、姿态角的滑模面及其一阶导数,设计出位置控制器和姿态角控制器,过程如下:
3.1,定义位置跟踪误差及其一阶微分和二阶微分:
其中i=1、2、3,x1=x,x2=y,x3=z,x1d表示x的期望信号,x2d表示y的期望信号,x3d表示z的期望信号,e1表示x的位置跟踪误差,e2表示y的位置跟踪误差,e3表示z的位置跟踪误差;
3.2,定义位置的滑模面:
其中ci为正常数,s1为x的滑模面,s2为y的滑模面,s3为z的滑模面;
3.3,分别对式(8)两边进行求导,得滑模面的一阶导数为
把式(7)代入式(9),得到
把式(5)代入式(10),得到
其中u1=ux,u2=uy,u3=uz;
3.4,选择趋近律滑模
其中
联立式(10)、式(11),得到位置控制器的输入:
3.5,根据式(6)解耦出合外力ur,和姿态角的期望值φd、θd,定义姿态角的跟踪误差及其一阶微分和二阶微分:
其中j=4、5、6,x4=φ,x5=θ,x6=ψ,x4d表示φ的期望信号,x5d表示θ的期望信号,x6d表示ψ的期望信号,e4表示φ的跟踪误差,e5表示θ的跟踪误差,e6表示ψ的跟踪误差;
3.6,定义姿态角的滑模面:
其中cj为正常数,s4为φ的滑模面,s5为θ的滑模面,s6为ψ的滑模面;
3.7,分别对式(14)两边进行求导,得姿态角的滑模面的一阶导数为
把式(13)代入式(15),得到
把式(5)代入式(16),得到
其中uj为姿态角控制器的输入,u4=τx,u5=τy,u6=τz,
3.8,选择趋近律滑模
其中
联立式(17)、式(18),得到姿态角控制器的输入:
进一步,所述增强型双幂次趋近律滑模控制方法还包括以下步骤:
步骤4,证明滑动模态可以在有限时间到达平衡零点附近,同时验证增强型双幂次趋近律的到达时间小于传统双幂次趋近律的到达时间,过程如下:
4.1,设计李雅普诺夫函数
其中
由于d(s)>0,则
4.2与传统双幂次趋近律滑模控制方法比较到达时间,过程如下:
对于增强型双幂次趋近律,当初始位置s(0)>1时,对于s(0)→s=1的过程中,第一项起主导作用,因此有式(19)
当初始位置s(0)<-1时,对于s(0)→s=-1的过程中,第一项起主导作用
联立(20),(21)对于s(0)→sign[s(0)]的过程中,得(22)
其中|s(0)|>1;
对于传统双幂次趋近律,s(0)→sign[s(0)]的过程中的到达时间为
因此,在s(0)→sign[s(0)]的过程中,增强型双幂次趋近律的到达时间比传统双幂次趋近律的到达时间更短;
同理,在sign[s(0)]→0的过程中,第二项起主导作用
增强型双幂次的到达时间为
传统双幂次趋近律的到达时间为
因此,在sign[s(0)]→0的过程中,增强型双幂次趋近律的到达时间比传统双幂次趋近律的到达时间更短;
综上所述,增强型双幂次趋近律的到达时间比传统双幂次趋近律的到达时间更短。
为验证所提方法的有效性,本发明给出了增强型双幂次趋近律滑模控制方法和传统双幂次趋近律滑模控制方法的对比:
为了更有效的进行对比,系统所有参数都是一致的,即x1d=x2d=x3d=2,x6d=0.5,g=10;滑模面参数:c1=c2=c3=2,c4=c5=c6=2,k11=k12=k13=0.2,k14=k15=k16=0.7,k21=k22=k23=0.2,k24=k25=k26=0.9,α1=α2=α3=α4=α5=α6=1.4,β1=β2=β3=β4=β5=β6=0.7;增强型双幂次趋近律中d(s)项参数:δ1=δ2=δ3=δ4=δ5=δ6=0.5,γ1=γ2=γ3=γ4=γ5=γ6=0.6,p1=p2=p3=p4=p5=p6=1;四旋翼无人机的参数:m=0.625,l=0.1275,ixx=2.3×10-3,iyy=2.4×10-3,izz=2.6×10-3,l=0.1275,kf=2.103×10-6,km=2.091×10-8;采样参数:ts=0.007,n=1000;
从图7和图8中我们可以看出,增强型双幂次趋近律比传统双幂次趋近律能够更快地到达滑模面;再结合图1和图2,我们可以看出增强型双幂次趋近律控制下的四旋翼无人机比传统双幂次趋近律控制下的四旋翼无人机更快地到达指定位置。
综上所述,增强型双幂次趋近律滑模控制比传统双幂次趋近律滑模控制有着更短的到达时间,从而使系统更快地进入稳定收敛。
以上阐述的是本发明给出的一个实施例表现出的优良优化效果,显然本发明不只是限于上述实施例,在不偏离本发明基本精神及不超出本发明实质内容所涉及范围的前提下对其可作种种变形加以实施。
- 还没有人留言评论。精彩留言会获得点赞!