一种面向多工序制造过程的工艺可靠性评估及控制方法与流程

本发明涉及一种面向多工序制造过程的工艺可靠性评估及控制方法，属于生产控制领域。

背景技术：

现代大型装备产品结构复杂，其制造过程包含多个工序。在各工序制造过程中，输出产品的质量受多种误差源作用的影响而产生偏差，最终影响到产品的使用性能。对工艺可靠性进行实时地计算评估，并加以控制，保障工艺系统稳定地运行，是实现产品质量控制的重要手段。然而多工序制造过程中误差产生和演化机理十分复杂，如何对工艺可靠性进行实时把控，以便能够即时、准确地诊断工艺系统故障，已成为工程人员面临的棘手难题。

当前，针对产品生产过程质量控制的相关理论和方法诸多，但它们在面向多工序制造过程质量控制时存在一些弊端。其中，控制图方法作为一种被广泛使用的产品过程质量控制手段，通过对产品质量特性进行实时测量、监控来控制工艺过程。该方法具备易于操作、控制及时等优点，但它未考量输入工序的待加工件特性，面向具有误差传递累积特性的多工序过程、产品质量特性值发生异常偏移时，该方法无法对误差源头进行判定。而另一类基于误差流(sov)模型的质量控制方法，其数学模型适用于单一零件的多工序制造过程，在面向具有统计特性的大批量产品时，该方法适用性不强。

技术实现要素：

针对现有技术中质量控制方法存在的下述不足：无法兼顾精确识别误差源头和面向大批量零件进行质量控制。本发明公开的一种面向多工序制造过程的工艺可靠性评估及控制方法要解决的技术问题是：能够精确识别误差源头，且能够面向大批量零件进行质量控制，进而提高多工序制造过程的工艺可靠性和质量，具有涵盖的控制过程范围全面的优点。

本发明的目的是通过下述技术方案实现的。

本发明公开的一种面向多工序制造过程的工艺可靠性评估及控制方法，首先通过建立系数矩阵以及转移概率矩阵来构造误差传递概率方程；接着对工艺可靠度进行定义，分别评估多工序实际工艺可靠度、各单工序理想工艺可靠度以及毛坯件基准可靠度，以此反映多工序过程中存在的质量薄弱环节，对质量薄弱环节工序质量进行改善后返回建立符合当前情况的误差传递概率模型；最后基于z检验对工艺可靠性状态进行持续监测，先检验多工序过程、失控时再检验各单工序过程，确定故障工序并对工序质量进行调整后返回建立符合当前情况的误差传递概率模型。迭代上述过程，当检验结果表明多工序过程工艺可靠性状态受控，多工序制造过程能够实现保证预设质量要求下的持续生产，即实现面向大批量零件的质量控制，进而实现多工序制造过程工艺可靠性的保障和提升。

本发明公开的一种面向多工序制造过程的工艺可靠性评估及控制方法，包括如下步骤：

步骤一：建立多工序制造过程误差传递概率模型。

依据多工序制造过程的工艺方案，梳理各工序中制造特征-基准特征关系。面向制造特征-基准特征关系、基于制造过程中质量特性-基准特性作用函数建立理想质量特性误差随基准特性误差变化的系数矩阵γi(k)，并依据制造过程中工艺设备的相关参数建立实际质量特性误差随理想质量特性误差的转移概率矩阵pi(k)。再通过构建误差传递概率方程对批量产品的误差传递过程进行数学表达，所述的误差传递概率方程即为多工序制造过程误差传递概率模型，同时具备统计性描述以及适用于多工序过程、可递推的特点。

步骤一中：所述的面向制造特征-基准特征关系、基于制造过程中质量特性-基准特性作用函数建立理想质量特性误差随基准特性误差变化的系数矩阵γi(k)，如公式(1)所示，

式中，n表示工件所具有的质量特性数量，k为工序道数，表示第k道工序产出的质量特性值xi(k)对某基准值的偏导数。

所述的实际质量特性误差随理想质量特性误差的转移概率矩阵pi(k)，如公式(2)所示，

式中，表示产品的质量特性误差的从理想状态a转移到实际状态b的概率，每种状态为一取值区间。

所述的误差传递概率方程，如公式(3)所示，

式中，δx(·)n×m为产品质量特性误差的概率分布矩阵，a(·)n×n为未发生制造变化的质量特性的选择矩阵，bi(·)n×n为发生制造变化的质量特性i的选择矩阵，γi(·)为制造过程的系数矩阵，f(γi(k)1×n,bi(k)n×n×δx(k-1)n×m)n×m为仅考虑基准特性误差的理想质量特性误差，pi(·)m×m为受工艺过程作用的误差转移概率矩阵。

步骤二：评估工艺可靠性。

以工艺可靠度来量化工艺可靠性，将工艺可靠度定义为：在一定时间内、在输入一定质量毛坯件的情况下，制造系统最终产出产品的质量符合工艺参数质量的概率。依据多工序制造过程误差传递概率模型计算得到各工序产出产品各项质量特性的统计分布规律，累加某项质量特性符合工艺参数的区间概率得到该项质量特性的工艺可靠度，累乘产品具有的各项质量特性工艺可靠度得到工序的工艺可靠度。分别计算多工序实际工艺可靠度r'、各单工序理想工艺可靠度r(k)”以及毛坯件基准可靠度多工序实际工艺可靠度r'基于实际的毛坯件基准误差分布求解得到，单工序理想工艺可靠度r(k)”基于无基准误差的理想情况求解得到，毛坯件基准可靠度由多工序实际工艺可靠度r'除以各单工序理想工艺可靠度r(k)”累乘之积得到。单工序理想工艺可靠度r(k)”剔除了基准误差的影响能够反映单工序过程本身的制造能力，毛坯件基准可靠度能够反映毛坯件基准误差对最终产品可靠度的影响。将多工序过程中各单工序理想可靠度r(k)”以及毛坯件基准可靠度进行比较，比较结果反映多工序过程中的质量薄弱环节，对未符合预期的质量薄弱环节的工序质量进行改善后，返回步骤一建立符合当前情况的误差传递概率模型，以便重新评估。

步骤二中所述的工序的工艺可靠度r(k)，如公式(4)所示：

△x(k)i·为公式(3)中δx(k)n×m的第i行元素，△ui∈t表示第i项质量特性符合工艺参数公差。

所述的毛坯件基准可靠度如公式(5)所示：

步骤三：控制工艺可靠性。

对工艺可靠性进行控制，即在输入毛坯件质量一定的情况下，对工序过程质量进行控制，从而保证最后输出产品的质量。将工艺可靠性的状态分为受控或失控，基于z检验对工艺可靠性状态进行检测。实际操作时，首先对多工序制造过程进行检验，如检验结果表明多工序过程工艺可靠性状态失控，再通过对各单工序工艺可靠性状态进行检验，确定故障工序并对相应工序的工序质量进行改善，改善后需返回步骤一建立符合当前情况的误差传递概率模型。

步骤三中所述的基于z检验对工艺可靠性状态进行检测，具体实现方法如下：当工艺可靠性状态处于受控状态，抽取工件样本，测量工件样本制造前的基准特性误差及制造后的质量特性误差；将基准特性误差代入误差传递概率模型计算得到质量特性误差预期的概率分布矩阵δx(k)n×m，将所得矩阵的概率分布以及实测的质量特性误差值统一归一到标准正态分布下进行检验；若样本中产品实际的质量特性误差的概率分布与经步骤一误差传递概率模型计算得到的预期概率分布不存在显著性差异，表明工艺可靠性状态受控，否则表明工艺可靠性状态失控。

步骤四：迭代步骤一到步骤三，实现面向大批量零件的质量控制。

对步骤一到步骤三进行迭代。对步骤二中未符合预期的质量薄弱环节的工序质量进行改善后，返回步骤一建立符合当前情况的误差传递概率模型。当步骤三中检验结果表明多工序过程工艺可靠性状态失控，再通过对各单工序工艺可靠性状态进行检验，确定故障工序，对故障工序的工序质量进行改善后，返回步骤一建立符合当前情况的误差传递概率模型。当步骤三中检验结果表明多工序过程工艺可靠性状态受控，多工序制造过程能够实现保证预设质量要求下的持续生产，即实现面向大批量零件的质量控制，进而实现多工序制造过程工艺可靠性的保障和提升。

有益效果：

1、本发明公开的一种面向多工序制造过程的工艺可靠性评估及控制方法，建立多工序制造过程误差传递概率模型，误差传递概率模型具备统计性描述以及适用于多工序过程、可递推的特点，基于该模型对工艺可靠性进行评估及控制，能够精确识别误差源头，且能够面向大批量零件进行质量控制，即具有更好的诊断性和适用性。

2、本发明的一种面向多工序制造过程的工艺可靠性评估及控制方法，由于包括生产前的工艺可靠度的评估以及生产中、生产后工艺可靠性状态的持续监测和控制，所以涵盖的控制过程范围全面。

附图说明

图1为本发明公开的一种面向多工序制造过程的工艺可靠性评估及控制方法的流程图；

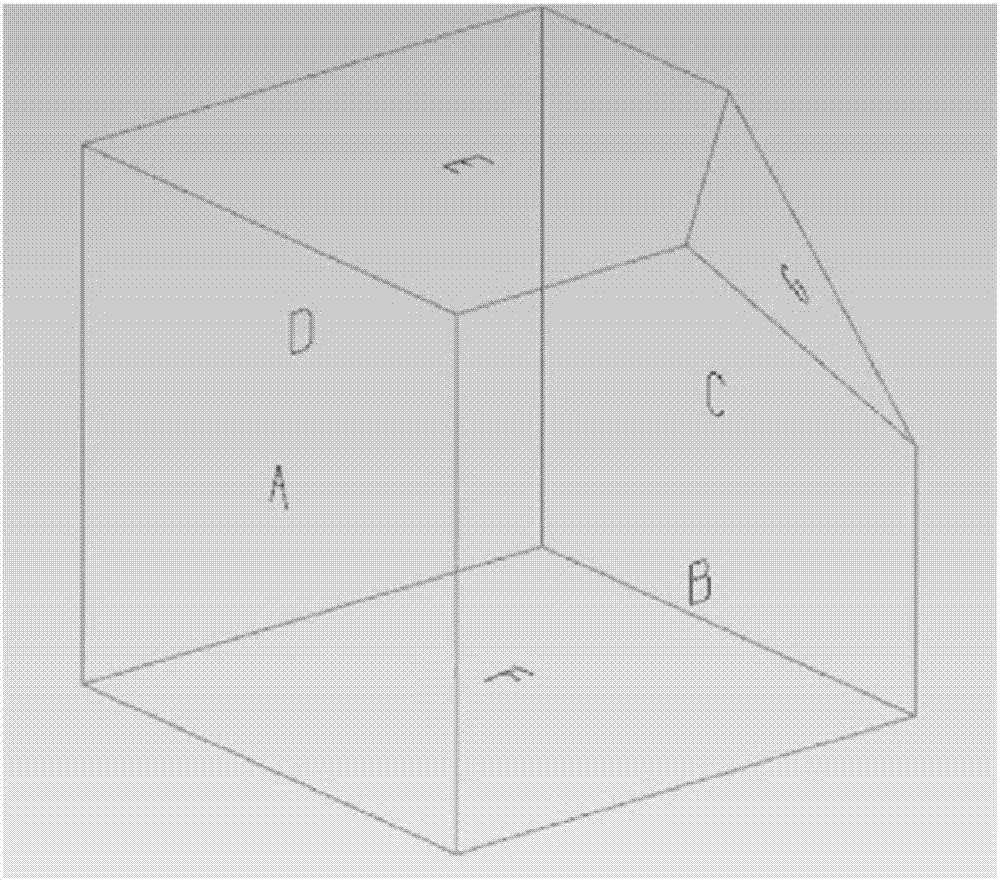
图2为工件三维形状示意图；

图3为制造特征-基准特征关系网状图；

图4为各可靠度间的串联关系。

具体实施方式

为了验证方法的可行性，下面结合附图与“面向某工件的制造过程”实施例对本发明作进一步说明：

实施例1

本实施例公开的一种面向多工序制造过程的工艺可靠性评估及控制方法，方法的流程图如图1所示，具体步骤如下：

步骤一：建立多工序制造过程误差传递概率模型。

依据某工件(如图2所示)的工艺方案：

工序1、以a+c+f为定位面(f为主定位面)，铣削面e，去除量为2mm，得到新的表面e1；

工序2、以e1+b+d为定位面(e1为主定位面)，铣削f面，去除量为2mm，得到新的表面f1；

工序3、以f1+b+d为定位面(f1为主定位面)，铣削g面，去除量为1mm，得到新的表面g1。

梳理各工序中制造特征-基准特征关系，如图3所示。前道工序制造的特征面可能会被用作后道工序的定位基准面，质量特性误差沿此关系在多工序制造过程中产生累积传递作用。

该工件共具有8个质量特性，对于制造过程中的第k道工序，面向制造特征-基准特征关系、基于该工序制造过程中质量特性-基准特性作用函数建立理想质量特性误差随基准特性误差变化的系数矩阵γi(k)，并依据生产状态下工艺设备的相关参数建立实际质量特性误差随理想质量特性误差的转移概率矩阵pi(k)。再通过构建误差传递概率方程对批量产品的误差传递过程进行数学表达，所述的误差传递概率方程即为多工序制造过程误差传递概率模型。

步骤一中：所述的面向制造特征-基准特征关系、基于制造过程中质量特性-基准特性作用函数建立理想质量特性误差随基准特性误差变化的系数矩阵γi(k)，如公式(1)所示，

式中，k为工序道数，表示第k道工序产出的质量特性值xi(k)对某基准值的偏导数。

所述的实际质量特性误差随理想质量特性误差的转移概率矩阵pi(k)，如公式(2)所示，

式中，表示产品的质量特性误差的从理想状态a转移到实际状态b的概率，每种状态为一取值区间。此概率与工序中设备的状态参数有关，与输入工序产品的基准特性参数无关。

所述的误差传递概率方程，如公式(3)所示，

式中，δx(·)8×m为产品质量特性误差的概率分布矩阵，a(·)8×8为未发生制造变化的质量特性的选择矩阵，bi(·)8×8为发生制造变化的质量特性i的选择矩阵，γi(·)为制造过程的系数矩阵，f(γi(k)1×8,bi(k)8×8×δx(k-1)8×m)8×m为仅考虑基准特性误差的理想质量特性误差，pi(·)m×m为受工艺过程作用的误差转移概率矩阵。

步骤二：评估工艺可靠性。

依据多工序制造过程误差传递概率模型可计算得到产出产品各项质量特性的统计分布规律，累加某项质量特性符合工艺参数的区间概率得到该项质量特性的工艺可靠度，累乘产品具有的各项质量特性工艺可靠度得到工序的工艺可靠度r(k)。分别计算多工序实际工艺可靠度r'、各单工序理想工艺可靠度r(k)”以及毛坯件基准可靠度它们间的串联关系如图4所示，多工序实际工艺可靠度r'基于实际的毛坯件基准误差分布求解得到，单工序理想工艺可靠度r(k)”基于无基准误差的理想情况求解得到，毛坯件基准可靠度由多工序实际工艺可靠度r'除以各单工序理想工艺可靠度r(k)”累乘之积得到。将多工序过程中各单工序理想可靠度r(k)”以及毛坯件基准可靠度进行比较，比较结果反映多工序过程中的质量薄弱环节，对未符合预期的质量薄弱环节的工序质量进行改善后，返回步骤一建立符合当前情况的误差传递概率模型，以便重新评估。

步骤二中所述的工序的工艺可靠度r(k)，如公式(4)所示：

△x(k)i·为公式(3)中δx(k)8×m的第i行元素，△ui∈t表示第i项质量特性符合工艺参数公差。

所述的毛坯件基准可靠度如公式(5)所示：

步骤三：控制工艺可靠性。

将工艺可靠性的状态分为受控或失控，基于z检验对工艺可靠性状态进行检测。首先对多工序制造过程进行检验，如检验结果表明多工序过程工艺可靠性状态失控，再通过对各单工序工艺可靠性状态进行检验，确定故障工序并对相应工序的工序质量进行改善，改善后需返回步骤一建立符合当前情况的误差传递概率模型。

步骤三中所述的基于z检验对工艺可靠性状态进行检测，具体实现方法如下：做出假设“工艺可靠性状态处于受控状态”，即抽取样本中产品实际的质量特性误差的概率分布与经步骤一误差传递概率模型计算得到的预期概率分布不存在显著性差异。抽取10个工件，测量它们制造前的基准特性误差及制造后的质量特性误差。将基准特性误差代入公式(3)计算出质量特性误差预期的概率分布矩阵δx(·)8×m，由于产品质量误差往往服从正态分布，将所得矩阵的概率分布以及实测的质量特性误差值统一归一到标准正态分布下，以便能在同一基准下对此样本中10个工件的制造过程工艺可靠性状态进行z检验。经过检验后，若假设成立，表明工艺可靠性状态受控；否则表明工艺可靠性状态失控。

步骤四：迭代步骤一到步骤三，实现面向大批量零件的质量控制。

对步骤一到步骤三进行迭代。对步骤二中未符合预期的质量薄弱环节的工序质量进行改善后，返回步骤一建立符合当前情况的误差传递概率模型。当步骤三中检验结果表明多工序过程工艺可靠性状态失控，再通过对各单工序工艺可靠性状态进行检验，确定故障工序，对故障工序的工序质量进行改善后，返回步骤一建立符合当前情况的误差传递概率模型。当步骤三中检验结果表明多工序过程工艺可靠性状态受控，多工序制造过程能够实现保证预设质量要求下的持续生产，即实现面向大批量零件的质量控制，进而实现多工序制造过程工艺可靠性的保障和提升。

以上所述的具体描述，对发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。