一种不确定信息下多无人机空战动态博弈方法与流程

本发明涉及一种不确定信息下多无人机空战动态博弈方法，属于飞机试验及无人机技术领域。

背景技术：

现代战场上的信息越来越复杂，博弈论应用于多无人机空战作战中，已引起国内外军事专家的关注，也成为军事决策在复杂的战场信息变量理论。多无人机空战博弈的分类根据不同的基准可以有不同的分类。一般认为，多无人机空战博弈主要可以分为合作博弈和非合作博弈。从无人机空战行为的时间序列来说，多无人机空战博弈论进可分为静态空战博弈、动态空战博弈。从敌空战我无人机对彼此信息的了解程度来说分为完全信息空战博弈和不完全信息空战博弈。从多无人机空战博弈进行的次数或者持续长短来说可以分为有限空战博弈和无限空战博弈。从多无人机空战博弈的逻辑基础不同来说可以分为传统空战博弈和演化空战博弈等。随着现代空中飞行器机载传感器探测识别技术突破性的改进，使得军事指挥人员能够更全面的了解作战信息以至于更加有效地指挥军事博弈。在多无人机空战完全信息博弈中，当敌我无人机进行实时攻击防御对抗作战时，如何在了解彼此作战信息、作战策略、作战要素等关键信息下快速准确的选择最优空战策略，实时的做出明智的决定，对无人机空战博弈的最终结果影响至关重要。

目前，国内外学者对于无人机空战博弈问题进行了大量的研究，并且得到了很多有价值的成果，但是仍然存在许多问题需要解决。

①关于完全信息下多无人机攻防对抗博弈研究较多，而对于不完全信息下无人机攻防对抗研究较少。

②关于多无人机攻防对抗采用静态博弈方法较多，而采用动态博弈方法研究较少。

③关于多无人机空战采用完全且完美信息博弈方法较多，而关于在不确定信息下对无人机空战博弈实时策略动态规划研究较少。

技术实现要素：

本发明的目的在于提供一种不确定信息下多无人机空战动态博弈方法；现阶段通过对国内外多无人机攻击分析和研究方法的总结，针对博弈，虽然多无人机空战博弈方法做了大量研究国内外学者，建立了不同的多无人机空战博弈模型，并提出了不同的需求矩阵博弈的纳什均衡值该方法基本，但并非是基于这方面的不确定性信息。由于现代战场的复杂性，要求决策者必须考虑各种不确定性因素的动态变化情况，使决策方案是可行的，以满足实际需要。

1、针对目标价值和打击概率的不确定信息问题，提出了基于不确定信息的无人机空战动态博弈策略方法。首先通过分析无人机空战态势和作战信息的不确定性，建立不确定信息下的多无人机动态博弈的收益函数，构建基于不确定信息的双方博弈支付矩阵；然后，通过将动态扩展式博弈转化成静态战略式博弈，最后，求出不确定信息下的动态博弈的混合策略纳什均衡解。

2、针对空战过程中的双方作战收益的不确定性问题，提出了基于模糊支付的无人机空战动态博弈策略方法。首先通过分析无人机空战态势信息的不确定性，建立模糊信息下的多无人机动态博弈的作战优势函数，将动态扩展式博弈转化成静态策略式博弈，构建基于模糊信息的双方博弈的支付矩阵；最后给出模糊信息下动态博弈的混合战略的纳什均衡求解方法。

本发明为了实现上述目的，采用如下技术方案：

一种不确定信息下多无人机空战动态博弈方法：

(1)、建立无人机空战动态博弈策略集；

在空战中，将敌方和我方无人机分别看作博弈的两个局中人，采取k阶段动态博弈对抗；

基于不确定信息的多无人机空战动态博弈模型可表述为：其中：n＝{1,2}，为博弈中的2个参与人，结点1代表我方无人机群，结点2代表敌方无人机群；

为博弈中参与者行动空间：行动集，为我方无人机第k阶段选择第i种的行动策略，为敌方无人机第k阶段选择第j种的行动策略；

为参与无人机可能选择的每一行动组合所相对应的各参无人机的收益区间；

(2)、建立敌我双方无人机支付函数；

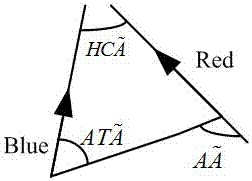
在空战中，要想对敌方飞机进行打击，就要占据有利的攻击位置，同时使己方进攻风险降到最低，考虑双方飞行器动力学和假设敌方策略，构建空战一对一态势几何图；

aa为双方视线角，|aa|＜180°；hca头顶交叉角，ata为目标进入角，|ata|＜180°；

(3)、函数之间的状态转移；

当无人机执行完第k-1阶段后，到第k阶段时，该阶段的无人机为i＝f(h)，表示该阶段轮到无人机i执行策略；此时，参与者i选择策略s^k前战场状态为执行策略s^k后预期战场状态为

战场态势由角度状态和距离状态组成，并由此设定此空战态势下的区间态势评估函数为为无人机i对无人机j的空战区间态势评估，分别为对角度状态和距离状态的评估；

(4)、求解区间信息下动态博弈纳什均衡；

根据区间可能度公式对不确定信息下的敌我双方的支付矩阵进行计算，最后利用粒子群算法求出不确定信息下纳什均衡值。

(5)、建立系统界面，给出不确定信息下多无人机空战动态博弈作战策略。

进一步的，在步骤(1)中：

无人机空战博弈树中，无人机i在第k阶段博弈中的行动情形可以用一个信息集表示，因此无人机的行动策略实际上就是无人机在每个信息集上的行动规则；

用hi表示博弈树中无人机i的信息集ii的集合，即hi＝{ii}；用ai(ii)表示无人机i在信息集ii上的行动集，ai(hi)表示无人机i在所有信息集上的行动集合，即：

所以无人机i的纯策略集可以用无人机i在每个信息集上的行动集的笛卡尔积来表示。

进一步的，在步骤(2)中：

假设敌我双方无人机在水平方向速度固定，这里只考虑角度与距离，构建空战态势优势函数：

式中，r为两机之间为实际距离，rd为两机之间期望距离，即在雷达扫描范围内；k为常数，这里取0.1，单位米/角度，用来调整距离与角度的影响效果；

在对实际空战综合态势进行分析后，每个因素都存在一定变化区间，这里只考虑角度和距离变化的影响，即：从而导致

假设我方无人机集合为m＝{1，2，…，i，…，m}，由于战场战场的不确定性其区间价值集合为同样敌方无人机集合为n＝{1,2,…,j,…,n}，其区间价值集合为

设我方第i架无人机对敌方第j架命中概率为pwij，敌方第j架无人机对我方第i架命中概率为pdij，则我方第i架无人机攻击敌方第j架无人机的收益函数rwij为：

式中vdmax为敌方无人机价值集合中的最大价值；

同理，敌方第j架无人机攻击敌方第i架无人机的收益函数rdji为：

综合上述多无人机空战态势优势函数和作战能力优势函数，可得我方在不确定信息下的多无人机空战的总体优势函数为：

式中,k1,k2为加权系数,且k1+k2＝1。

同理，敌方在不确定信息下的多无人机空战的总体优势函数为：

博弈中的支付是指参与人在进行策略选择时的最终所得或损失；

在空战中我方无人机的收益，必然是敌方无人机的损失，即构成敌我双方无人机零和博弈模型；则不确定信息下多无人机空战博弈支付函数为：

式中，xij,yij分别为二值决策变量，xij＝1表示我方第i架无人机去攻击敌方第j架无人机，xij＝0表示第i架无人机没有被分配去攻击敌方第j架无人机；

同样，yij＝1表示敌方第j架无人机攻击我方第i架无人机，yij＝0表示敌方第j架无人机没有攻击我方第i架无人机；

可得不确定信息下无人机空战博弈支付矩阵为：

式中，x1,x2,…,xm分别为我方无人机所采取策略；y1,y2,…yn分别为敌方无人机所采取策略，为我方无人机采取第xi种策略，敌方无人机采取第yj种策略时我方无人机的收益。

进一步的，在步骤(4)中：区间可能度矩阵基本概念；

定义1：对于任意的两个区间数a＝[a^l,a^r]，b＝[b^l,b^r]，则区间数大于的可能度为：

同样，大于的可能度为：

定理1：设为由式(1a)或式(1b)确定的的可能度，则与具有互补性，即

定义2：对于所有任意区间数两两进行比较，可得到区间数可能度矩阵p为：

其中，pij表示的可能度。

进一步的，在步骤(4)中：基于区间可能度的混合策略纳什均衡分析；

定义3：设博弈参与人n的集合，对于每个i∈n，参与人i的纯策略集为若参与人i都以概率对每一个纯策略进行选择，则称为参与人i的一个混合策略；

定义4：设是非合作博弈g的一个混合策略局势。如果对于每一个i∈n和每个xi∈xi,都有：

ei(x^*)≤ei(xi),i＝1,2,…,n(13)

则称x^*是非合作博弈g的一个混合策略纳什均衡，{ei(x^*)}为其对应的均衡期望收益值；

由上面所述，可知式(13)中的e(x)为区间数，所以设为我方采取第xk策略时敌方分别采取y1,y2,…yn策略时我方无人机的支付值，根据式(10)、(11)，通过区间支付值的两两比较，可得可能度矩阵p:

其中，pji＝1-pij,i,j∈{1,…,m},i≠j,pii＝('-')表示对于区间支付值自身相比不需要给出任何比较信息，pij值是用来描述区间支付值优于区间支付值的程度，当pij＝0时，绝对优于当pij＝1时，绝对优于

对区间支付值进行优劣排序，通过两两进行比较，可得区间支付值的可能度矩阵p，对各个区间支付值进行排序，然后根据定义4得到最优期望值ei(x^*)，ei(x^*)即为混合策略纳什均衡值。

进一步的，在步骤(4)中：区间信息下基于粒子群算法的纳什均衡值求解；

设局中人1的混合策略为x＝(x1,x2,···xm)，可得纳什均衡值

传统的单矩阵博弈纳什均衡可以转化为采用线性规划问题进行求解，在不确定信息下的每种策略方案所对应的收益均为区间数值，则令将式(15)转换为下面的数学规划问题：

求解单矩阵博弈的纳什均衡就是求解线性规划式(16)的最优解；

上述为粒子群算法基础之上求解区间支付博弈矩阵的纳什均衡值；

算法中的每个个体最优粒子更新方式如下；设pid(t)为上一代个体最优粒子，pid(t+1)为当前状态下个体最优粒子，xi(t+1)为新产生的粒子，如果则pid(t+1)＝xi(t+1)，其中表示适应度函数，如果则pid(t+1)＝pid(t)；

利用粒子群算法求解区间支付博弈矩阵的纳什均衡值流程步骤为：

步骤1：粒子的位置进行初始化设置，确定粒子维数d和种群规模m；

步骤2：把当前的粒子看做最优个体，对每个粒子的适应度值进行求解，然后根据区间数的排序方法，求得个体最优粒子pid；

步骤3：对求出的每个粒子适应度进行比较，得到新的个体最优粒子pid，将所有的个体最优粒子进行比较得到新的全局最优粒子pgd；

步骤4：重复步骤3、步骤4，更新全局最优粒子pgd；

步骤5：若达到最大迭代次数，计算结束，输出全局最优解，否则转向步骤2。

本发明的有益效果：本发明为多无人机作战的不完全信息动态博弈模型方法，为中国的无人作战飞机的发展做贡献，将博弈论应用到多无人机作战平台上，对提高自身的生存能力和作战效能具有重要的理论价值和实际意义。

附图说明

图1为本发明中无人机攻防对抗k阶段动态博弈树

图2为本发明中空战一对一几何态势分析图；

图3为本发明中我方适应度变化曲线；

图4为本发明中敌方适应度变化曲线。

具体实施方式

下面结合附图对本发明进行详细描述：

1、无人机空战动态博弈策略集

在空战中，将敌方和我方无人机分别看作博弈的两个局中人，采取k阶段动态博弈对抗，如图1所示。

因此，基于不确定信息的多无人机空战动态博弈模型可表述为：其中：n＝{1,2}，为博弈中的2个参与人，结点1代表我方无人机群，结点2代表敌方无人机群；为博弈中参与者行动空间(行动集)，为我方无人机第k阶段选择第i种的行动策略，为敌方无人机第k阶段选择第j种的行动策略；为参与无人机可能选择的每一行动组合所相对应的各参无人机的收益区间。

在图1无人机空战博弈树中，无人机i在第k阶段博弈中的行动情形可以用一个信息集表示，因此无人机的行动策略实际上就是无人机在每个信息集上的行动规则。用hi表示博弈树中无人机i的信息集ii的集合，即hi＝{ii}；用ai(ii)表示无人机i在信息集ii上的行动集，ai(hi)表示无人机i在所有信息集上的行动集合，即：所以无人机i的纯策略集可以用无人机i在每个信息集上的行动集的笛卡尔积来表示。

2、敌我双方无人机支付函数

在空战中，要想对敌方飞机进行打击，就要占据有利的攻击位置，同时使己方进攻风险降到最低。考虑双方飞行器动力学和假设敌方策略，构建空战一对一态势几何图，如图2。

图中aa为双方视线角，|aa|＜180°。hca头顶交叉角，ata为目标进入角，|ata|＜180°。

结合图2，假设敌我双方无人机在水平方向速度固定，这里只考虑角度与距离，构建空战态势优势函数：

式中，r为两机之间为实际距离，rd为两机之间期望距离，即在雷达扫描范围内。k为常数，这里取0.1，单位米/角度，用来调整距离与角度的影响效果。在实际空战环境中，各种干扰因素，往往不能精确地获得各种信息，在对实际空战综合态势进行分析后，每个因素都存在一定变化区间，这里只考虑角度和距离变化的影响，即：从而导致

假设我方无人机集合为m＝{1,2,…,i,…,m}，由于战场环境的不确定性其区间价值集合为同样敌方无人机集合为n＝{1,2,…,j,…,n}，其区间价值集合为设我方第i架无人机对敌方第j架命中概率为pwij，敌方第j架无人机对我方第i架命中概率为pdij，则我方第i架无人机攻击敌方第j架无人机的收益函数rwij为：

式中vdmax为敌方无人机价值集合中的最大价值。

同理，敌方第j架无人机攻击敌方第i架无人机的收益函数rdji为：

综合上述多无人机空战态势优势函数和作战能力优势函数，可得我方在不确定信息下的多无人机空战的总体优势函数为：

式中,k1,k2为加权系数,且k1+k2＝1。

同理，敌方在不确定信息下的多无人机空战的总体优势函数为：

博弈中的支付是指参与人在进行策略选择时的最终所得或损失。在空战中我方无人机的收益，必然是敌方无人机的损失，即构成敌我双方无人机零和博弈模型。则不确定信息下多无人机空战博弈支付函数为：

式中，xij,yij分别为二值决策变量，xij＝1表示我方第i架无人机去攻击敌方第j架无人机，xij＝0表示第i架无人机没有被分配去攻击敌方第j架无人机。同样，yij＝1表示敌方第j架无人机攻击我方第i架无人机，yij＝0表示敌方第j架无人机没有攻击我方第i架无人机。

可得不确定信息下无人机空战博弈支付矩阵为：

式中，x1,x2,…,xm分别为我方无人机所采取策略；y1,y2,…yn分别为敌方无人机所采取策略，为我方无人机采取第xi种策略，敌方无人机采取第yj种策略时我方无人机的收益。

3、函数之间的状态转移

当无人机执行完第k-1阶段后，到第k阶段时，该阶段的无人机为i＝f(h)，表示该阶段轮到无人机i执行策略。此时，参与者i选择策略s^k前战场状态为执行策略s^k后预期战场状态为

在式(3.4)中可知，战场态势由角度状态和距离状态组成，并由此设定此空战态势下的区间态势评估函数为为无人机i对无人机j的空战区间态势评估，分别为对角度状态和距离状态的评估。

随着时间的推移，当无人机执行完策略s^k，在第k+1阶段时，无人机i的态势状态转移为：

其中表示无人机i的角度状态区间，表示无人机i的距离状态区间，和分别表示角度状态区间和距离状态区间的变化量。

4、求解区间信息下动态博弈纳什均衡

根据区间可能度公式对不确定信息下的敌我双方的支付矩阵进行计算，最后利用粒子群算法求出不确定信息下纳什均衡值。

4.1区间可能度矩阵基本概念

定义1：对于任意的两个区间数a＝[a^l,a^r]，b＝[b^l,b^r]，则区间数大于的可能度为：

同样，大于的可能度为：

定理1：设为由式(1a)或式(1b)确定的的可能度，则与具有互补性，即

定义2：对于所有任意区间数两两进行比较，可得到区间数可能度矩阵p为：

其中，pij表示的可能度。

4.2、基于区间可能度的混合策略纳什均衡分析

定义3：设博弈参与人n的集合，对于每个i∈n，参与人i的纯策略集为若参与人i都以概率对每一个纯策略进行选择，则称为参与人i的一个混合策略。

定义4：设是非合作博弈g的一个混合策略局势。如果对于每一个i∈n和每个xi∈xi,都有：

则称x^*是非合作博弈g的一个混合策略纳什均衡，{ei(x^*)}为其对应的均衡期望收益值。

由上面所述，可知式(13)中的e(x)为区间数，所以设为我方采取第xk策略时敌方分别采取y1,y2,…yn策略时我方无人机的支付值，根据式(1)、(2)和式(3)，通过区间支付值的两两比较，可得可能度矩阵p:

其中，pji＝1-pij,i,j∈{1,…,m},i≠j,pii＝('-')表示对于区间支付值自身相比不需要给出任何比较信息，pij值是用来描述区间支付值优于区间支付值的程度，当pij＝0时，绝对优于当pij＝1时，绝对优于

对区间支付值进行优劣排序，通过两两进行比较，可得区间支付值的可能度矩阵p，对各个区间支付值进行排序，然后根据定义4得到最优期望值ei(x^*)，ei(x^*)即为混合策略纳什均衡值。

4.3区间信息下基于粒子群算法的纳什均衡值求解

设局中人1的混合策略为x＝(x1,x2,···xm)，可得纳什均衡值

传统的单矩阵博弈纳什均衡可以转化为采用线性规划问题进行求解，在不确定信息下的每种策略方案所对应的收益均为区间数值，则令将式(15)转换为下面的数学规划问题：

求解单矩阵博弈的纳什均衡就是求解线性规划式(16)的最优解。为了解决线性规划通常是简单的解决优化问题的传统方法，不能解决的不确定性区间数值博弈的纳什均衡的信息价值的问题，这是解决基于矩阵的区间支付混合策略问题非常困难。

本章是在粒子群算法(pso)基础之上求解区间支付博弈矩阵的纳什均衡值。

算法中的每个个体最优粒子更新方式如下；设pid(t)为上一代个体最优粒子，pid(t+1)为当前状态下个体最优粒子，xi(t+1)为新产生的粒子，如果则pid(t+1)＝xi(t+1)，其中表示适应度函数，如果则pid(t+1)＝pid(t)。

利用pso算法求解区间支付博弈矩阵的纳什均衡值流程步骤为：

步骤1：粒子的位置进行初始化设置，确定粒子维数d和种群规模m；

步骤2：把当前的粒子看做最优个体，对每个粒子的适应度值进行求解，然后根据区间数的排序方法，求得个体最优粒子pid；

步骤3：对求出的每个粒子适应度进行比较，得到新的个体最优粒子pid，将所有的个体最优粒子进行比较得到新的全局最优粒子pgd；

步骤4：重复步骤3、步骤4，更新全局最优粒子pgd；

步骤5：若达到最大迭代次数，计算结束，输出全局最优解，否则转向步骤2。

建立系统界面

最后，建立系统界面，给出不确定信息下多无人机空战动态博弈作战策略。