基于三段式路径规划的挠性卫星姿态控制方法与流程

本发明涉及卫星姿态控制技术领域，具体涉及一种卫星姿态快速机动控制方法，特别适用于具有挠性附件的卫星姿态大角度机动控制过程。

背景技术：

为增强在轨卫星的应用效能，提高敏捷卫星的快速机动能力及机动后的高稳定性是主要技术途径之一。在轨卫星结构与构型日趋复杂多样，整星的挠性特性越加明显，如安装大型太阳能帆板、天线等，这不仅影响机动的快速性，也影响机动后的姿态稳定性，如何兼顾卫星姿态控制的敏捷性及抑制挠性附件的振动是目前卫星姿态控制领域的主要课题之一。

通常，提高卫星姿态机动敏捷性需要采用大控制力矩的执行机构，如控制力矩陀螺或大型飞轮等。但卫星姿态机动时角加速度的剧烈变化会引起挠性附件的振动。因此，挠性卫星快速机动的需求可归纳为两点，一是要求卫星姿态机动到目标位置的时间尽可能短，姿态振动小；二是进入稳定的时间短，稳定精度高。同时卫星姿态机动过程中，除挠性附件的振动外，还受到许多不同的约束，如为保证敏感器有效工作而对角速度的约束、执行机构的力矩输出特性以及机动时间最优等，这些因素的限制使得姿态机动控制律的设计存在着困难和挑战。一种行之有效的控制方案是规划合理的姿态角位置、角速度及角加速度变化曲线，即设计姿态机动路径，并通过控制实现对规划路径的快速跟踪及高精度稳定。

技术实现要素：

本发明以金字塔构型cmg群为执行机构的挠性卫星为研究对象，提出一种融合三段式姿态路径规划与滚动优化跟踪的卫星姿态控制方法，以离线一次规划及在线滚动优化方式实现挠性敏捷卫星的姿态大角度快速机动及对挠性附件的振动抑制。

基于三段式路径规划的挠性卫星姿态控制方法，该方法由以下步骤实现：

步骤一、设定基准参考坐标系为惯性空间坐标系，建立以金字塔构型cmg群为执行机构具有挠性附件的卫星姿态动力学和运动学方程；并建立模态坐标系下的挠性附件振动动力学方程，通过定义新的状态变量，建立用于预测卫星姿态未来信息的非线性状态空间方程；

步骤二、根据当前时刻获得的卫星姿态及附件振动位移信息，通过离散化处理步骤一建立的非线性状态空间方程，获得挠性卫星姿态动力学和运动学的离散时间方程，采用所述离散时间方程进行未来预测时域np步的卫星姿态信息的预测；

步骤三、建立金字塔构型的cmg群动力学模型，获得cmg群输出力矩，根据雅克比矩阵引入奇异度量关系式，实时计算cmg群力矩输出的奇异性；

步骤四、基于正弦型角加速度的姿态路径规划方法，结合谱分析及优化算法，设计能够抑制挠性附件振动且机动时间最优的姿态轨迹；

所述基于正弦型角加速度的姿态路径规划方法为：基于正弦型函数设计三段式角加速度曲线，获得三段过程姿态机动时间关系；以机动时间为待优化目标，以角加速度和角速度为待优化变量，在满足机动过程中角加速度约束、角速度约束及避开挠性附件固有频率约束条件下，求解最优的挠性卫星姿态机动时间及相应的规划曲线；

步骤五、根据卫星姿态偏差、角速度偏差以及框架角速度偏差信息，建立卫星姿态机动过程优化指标，基于卫星系统动力学及运动学方程，离散化迭代计算未来预测时域内的卫星姿态信息，采用滚动时域控制方法实现卫星姿态跟踪控制；

步骤六、依据离散控制技术原理，在每个采样时刻重复步骤二至步骤五，通过反复更新卫星姿态信息，实现挠性卫星姿态机动的滚动优化控制。

本发明的有益效果：本发明通过将三段式角速度路径规划及非线性模型预测控制方法相互结合，提出一种基于三段式路径规划的挠性敏捷卫星姿态滚动优化控制方法。

一、建立了包含卫星姿态动力学、运动学及挠性附件振动的非线性状态空间方程，用于进行卫星姿态未来信息的准确预测。

二、基于三段式路径规划策略，对挠性卫星姿态机动时间进行最优设计，使得在完成卫星姿态机动目标情况下，规避挠性附件的振动。

三、采用非线性模型预测方法，以规划获得的姿态角速度曲线及姿态角位置曲线为期望跟踪目标，设计金字塔构型cmg群框架角速度的滚动优化跟踪控制律，实现抑制挠性附件振动的卫星姿态大角度快速机动控制。

四、本发明以离线一次规划及在线滚动优化方式实现挠性敏捷卫星的姿态大角度快速机动及对挠性附件的振动抑制。为带有挠性附件的卫星提供了一种融合规划与快速机动的控制策略，扩展了快速机动实现方式。

附图说明

图1为本发明所述的一种基于三段式路径规划的挠性敏捷卫星姿态滚动优化控制方法中挠性卫星姿态机动控制策略图；

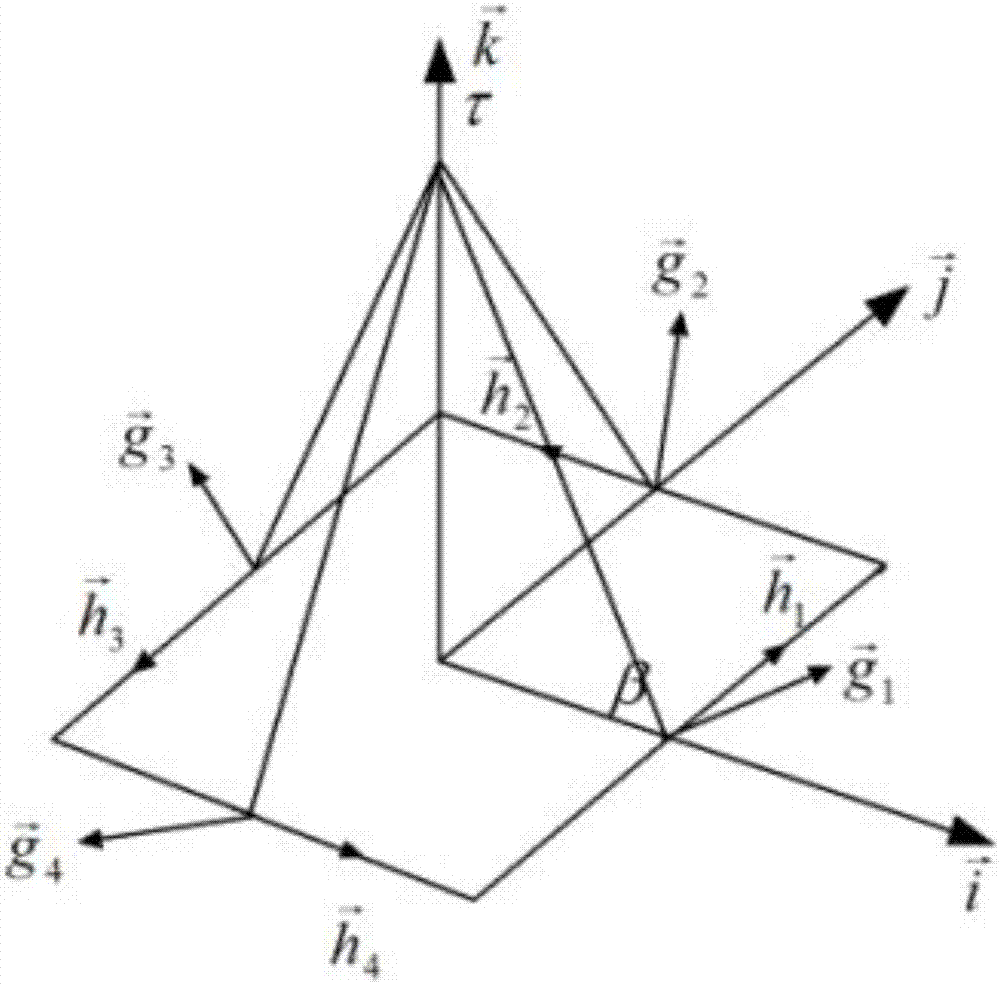
图2为本发明所述的一种基于三段式路径规划的挠性敏捷卫星姿态滚动优化控制方法中金字塔构型cmg群系统图；

图3为本发明所述的一种基于三段式路径规划的挠性敏捷卫星姿态滚动优化控制方法中姿态角加速度、角速度及角位置规划曲线图；

图4中图4a、图4b和图4c分别为本发明所述的一种基于三段式路径规划的挠性敏捷卫星姿态滚动优化控制方法中滚动轴姿态角加速度、角速度及角位置规划曲线示意图；

图5中图5a、图5b和图5c分别为本发明所述的一种基于三段式路径规划的挠性敏捷卫星姿态滚动优化控制方法中cmg群框架角位置、cmg群框架角速度及奇异性度量变化曲线示意图；

图6中图6a、图6b和图6c分别为本发明所述的一种基于三段式路径规划的挠性敏捷卫星姿态滚动优化控制方法中跟踪误差角、跟踪误差角速度及挠性附件振动位移变化曲线示意图。

具体实施方式

具体实施方式一、结合图1至图6说明本实施方式，一种挠性敏捷卫星姿态机动滚动优化控制方法，该方法由以下步骤实现：

步骤a：设定参考基准坐标系，建立以金字塔构型cmg群为执行机构具有挠性附件的卫星姿态动力学及运动学方程，并建立模态坐标系下的挠性附件振动动力学方程；通过定义新的状态变量，建立用于预测卫星姿态未来信息的非线性状态空间方程；

步骤b：根据当前时刻测得的卫星姿态信息，通过离散化后的非线性状态空间方程，对预测时域内的卫星姿态信息进行预测，建立卫星姿态的预测输出方程；

步骤c：建立金字塔构型cmg群动力学模型，获得cmg群系统输出力矩；根据雅克比矩阵引入奇异度量关系，实时计算cmg群力矩输出奇异性；

步骤d：基于正弦型角加速度的姿态路径规划方法，结合谱分析及优化算法，给出能够抑制挠性附件振动且机动时间最优的姿态轨迹；基于正弦型函数设计三段式角加速度曲线，获得三段过程姿态机动时间关系；以机动时间为待优化目标，以角加速度和角速度为待优化变量，在满足机动过程中角加速度约束、角速度约束及避开挠性附件固有频率约束条件下，求解最优的挠性卫星姿态机动时间及相应的规划曲线；

步骤e：以卫星姿态及角速度等的跟踪误差、框架角速度和终端偏差加权组合作为优化指标，以离散化的挠性卫星姿态动力学及运动学方程为基础，依据定姿系统输出的当前卫星信息，通过迭代计算获得未来预测时域内的卫星姿态信息；建立挠性卫星姿态跟踪控制的优化问题，实现规划卫星姿态跟踪的滚动时域控制。

步骤f：依据离散控制技术原理，在每个采样时刻重复步骤b至步骤e，通过反复更新卫星姿态信息，实现挠性卫星姿态机动的滚动优化控制。

具体实施方式二、结合图1至图6说明本实施方式，本实施方式为具体实施方式一所述的一种挠性敏捷卫星姿态机动滚动优化控制方法的实施例，其具体过程为：

一、以惯性坐标系为参考坐标系，建立姿态动力学方程为：

式中，js为卫星的转动惯量矩阵，w为星体三轴姿态角速度，σ为挠性附件与星体的刚柔耦合矩阵，η为挠性附件在模态坐标系下的位移，hcmg为金字塔构型cmg群的三轴角动量，td为空间干扰力矩。cmg群的控制力矩为其中[w×]表示为：

设定θx,θy,θz分别表征xyz转序下的滚动角、俯仰角和偏航角，进而卫星三轴姿态角速度w可以表示为：

式中，ax,ay,az表示相应的旋转矩阵。进一步有：

在模态坐标系下，挠性附件振动的动力学方程为：

式中，ζf为挠性附件模态的阻尼比矩阵，wf为挠性附件模态的振动频率矩阵。

融合卫星姿态动力学方程、运动学方程及挠性附件的振动方程，定义新的状态变量x＝[θηwwη]^t，忽略空间干扰力矩的影响，得到下式：

进而得到状态空间方程为：

该方程描述了卫星三轴姿态及角速度，挠性附件的振动位移及角速度的强非线性耦合关系。

综上，以金字塔构型cmg群为执行机构的挠性卫星姿态动力学及运动学可以归结为如下的非线性方程：

其中：

非线性函数f(x)描述了系统状态向量之间的相互影响及耦合关系。这里假设卫星的三轴姿态角速度、姿态角以及挠性附件在模态坐标系下的位移和速度均可通过测量或估计算法获得，定义系统的输出为yc＝x。进而有：

通过对以上连续时间系统进行离散化，可获得挠性卫星姿态动力学及运动学的离散时间方程如下：

根据当前时刻获得的卫星姿态及附件振动位移等信息，可用该方程进行未来一段时间内的卫星姿态等信息的预测。

二、本发明采用的cmg为单框架控制力矩陀螺，以金字塔构型安装，4个cmg对称分布，各框架轴在卫星本体坐标系中可表示为：

g1＝isinβ+kcosβ,g2＝jsinβ+kcosβ

g3＝-isinβ+kcosβ,g4＝-jsinβ+kcosβ(12)

式中，为第i个框架轴，β为安装倾角，为沿卫星本体坐标系三轴的基矢量。

金字塔构型cmg群系统的角动量h可表示为：

式中，为第i个cmg单元的输出角动量。

在卫星本体坐标系中有：

式中，δi为第i个cmg的框架角，hx,hy,hz为cmg群系统输出角动量在卫星本体三轴方向上分量，4个cmg的角动量均相同，不失一般性，假设为1。

对cmg群系统输出角动量h微分得到：

dh＝j1dδ1+j2dδ2+j3dδ3+j4dδ4＝jdδ(15)

式中，j为雅克比矩阵，形式为：

式中，ji表示第i个cmg单元输出的力矩矢量。

金字塔构型cmg群系统的输出力矩为：

式中，为cmg群系统的框架运动角速度。为衡量金字塔构型cmg群陷入奇异的情况，可引入奇异度量的定义：

当度量值越趋近于0时，表明其奇异性越大；当度量值越大时，表示离奇异面越远。在本方法中将以约束的形式对奇异性加以限制。

三、考虑到执行机构力矩输出能力、敏感器能够允许的最大角速度有限以及安全性等因素，姿态机动过程中的角加速度和角速度均会受到约束。采用基于正弦型角加速度的姿态路径规划方法，结合谱分析及优化算法，给出能够抑制挠性附件振动且机动时间最优的姿态轨迹。

基于正弦型函数设计的角加速度曲线按照时间分为三个过程，即加速段、匀速段和减速段。加速段采用开口向下的正弦型函数作为角加速度轨迹(周期为2tp)，匀速段的角加速度值设为零，减速段采用开口向上的正弦型函数作为角加速度轨迹，其幅值大小和频率与加速段轨迹相同。

设计角加速度机动路径规划曲线三个时间段方程分别为：

加速段：

匀速段：a(t)＝0

减速段：

通过对角加速度规划曲线进行一次积分，获得角速度机动路径规划曲线为：

加速段：

匀速段：v(t)＝v

减速段：

通过对角加速度规划曲线进行二次积分，获得角位置机动路径规划曲线为：

加速段：

匀速段：

减速段：

根据加速段、匀速段、减速段三段过程方程可知姿态角加速度、角速度及角位置规划曲线如图3所示，其中，a为角加速度，v为角速度，为每一时刻姿态角位置，为期望的机动姿态角位置，t2为匀速段时间，t1,t3分别为加速度及减速度时间，由加速段及减速段的对称性，有t1＝t3成立。

根据各阶段规划曲线在时间点t1、t1+t2和t1+t2+t3处的幅值关系，可计算出姿态机动时间为：

t＝t1+t2+t3(18)

其中：

以机动时间为待优化目标，以角加速度a和角速度v为待优化变量，在满足机动过程中角加速度约束、角速度约束及避开挠性附件固有频率约束条件下，建立优化问题如下：

式中，为机动控制任务期望的姿态角，vmax和amax分别为卫星姿态控制系统允许的最大机动角速度和角加速度，区间[f1,f2]表示为避开挠性附件振动频率而设计的正弦函数允许的频率范围。通过求解上式可获得最优的挠性卫星姿态机动时间及相应的规划曲线。

四、以步骤三规划的姿态角速度及角位置曲线为期望跟踪目标，以非线性挠性卫星姿态动力学及运动学方程为预测依据，设计金字塔构型cmg群框架角速度的滚动优化跟踪控制律。

将卫星姿态及角速度等的跟踪误差、框架角速度和终端偏差加权组合作为优化指标，定义如下：

式中：e(k+n)表示对最优轨迹等的跟踪误差，u(k+m)表示待设计的框架角速度。矩阵q,r,p为相应的跟踪误差、控制量和终端加权矩阵，np为预测时域，e(np)为预测时域np步数后卫星姿态及角速度的终端偏差。

以离散化的挠性卫星姿态动力学及运动学方程为基础，依据定姿系统输出的当前卫星信息，通过迭代计算，可计算未来np预测步内的卫星姿态信息：

式中，表示预测的卫星姿态输出。

从以上np步预测时域内的系统状态可知，预测后的待设计自由变量为np时间步内的控制量即待设计的金字塔构型cmg群框架角速度。当预测时域np超出控制时域nu时，假设群框架角速度在区间[nu,np]保持不变，即有：

此时，卫星姿态的预测输出方程为：

…

…

形成的挠性卫星姿态跟踪控制的优化问题如下：

且满足由执行机构的能力带来的时域约束条件：

式中，分别表示框架轴角速度的上界和下界，分别表示框架角速度增量的上界和下界。

目标函数整理为：

式中，表示预测的卫星姿态输出，r(k+n)为规划的卫星姿态信息。(q,r,p)为跟踪误差加权矩阵、框架角速度加权矩阵和终端加权矩阵。为系统的预测控制输入，即待优化的框架轴角速度，定义为：

式中，是互相独立的优化变量，记为：

假设卫星姿态跟踪控制的约束优化问题的最优解为：

根据预测控制原理，最优解的第一个元素，即当前时刻的框架轴角速度将作用于卫星姿态控制系统，定义当前时刻的当前控制量为：

在下一采样时刻，根据卫星姿态系统更新的状态信息，重复以上优化过程，实现规划卫星姿态跟踪的滚动时域控制。

本实施方式针对以金字塔构型cmg群为执行机构的挠性敏捷卫星，提出了一种融合轨迹规划与滚动优化跟踪思想的卫星姿态快速机动控制方法。以机动控制任务需求为依据，在考虑挠性附件振动抑制特性、敏感器工作允许最大角速度等约束条件下，基于正弦型曲线设计了最优的三段式姿态机动路径规划方法，该规划方法能够以非线性优化形式获得最优的轨迹参数；在奇异性及执行机构能力约束下，为实现对规划轨迹的快速跟踪，设计了cmg群框架轴角速度的非线性模型预测跟踪控制律，该控制律以在线滚动优化方式实现cmg群框架轴角速度的计算。

五、以某型挠性敏捷卫星为例，假设其测量的转动惯量矩阵为：

轨道选取为高度660km的太阳同步圆轨道，空间干扰力矩取为：

金字塔构型cmg群的转子角动量设定为5nms，每个cmg的最大框架角速度为2rad/s。考虑的金字塔构型cmg群的控制力矩约束为[-10nm，10nm]，其增量约束为[-0.15nm,0.15nm]。挠性附件的一阶振动频率取为0.32hz，阻尼比为0.032，刚柔耦合矩阵系数为[0.00041,3.833,0]。预测控制步数设定为30步，仿真步长设置为0.1s。考虑到姿态敏感器等有效工作的动态能力，机动过程中角速度的约束设定为[-3°/s,3°/s]，角加速度的约束为[-0.8°/s²,0.8°/s²]。

仿真结果见图4-图6。从图4规划曲线可以看出，敏捷卫星将在20.8905s内完成滚动轴姿态45°的快速机动，且机动的最大角速度为3°/s，稳态滑行时间为9.1095s。规划角加速度的频率为0.0849hz，远离挠性附件一阶频率，避免了机动时激起挠性附件的振动。从图5和图6的仿真曲线可以看出，在设计的框架角速度滚动跟踪控制律作用下，对规划姿态轨迹的跟踪误差角在机动过程中小于0.1°，误差角速度小于0.03°/s。在仿真时间20.8905s时，跟踪误差角小于0.05°，跟踪误差角速度小于0.002°/s。在整个机动过程中，挠性附件的振动幅值小于4×10^-7m。此外，cmg群框架角速度、角度及奇异约束等均满足设计的约束要求。