针对一类混合异质多智能体系统的分组一致性控制方法与流程

本发明属于智能控制领域，涉及一种针对一类混合异质多智能体系统的分组一致性控制方法。

背景技术：

多智能体系统一致性在生物、物理、机器人等领域受到密切关注，并得到广泛应用，目前已有很多研究成果。所谓一致性是指系统中智能个体的部分或者全部状态变量都收敛到某一个共同的值，而一致性控制是指利用智能个体与其邻居的相对或者绝对信息设计分布式的控制协议实现一致性。在工程实践中，智能个体往往是异质的，具有不同的动力学特性。因此，研究由异质智能个体组成的混合多智能体系统具有重要的理论价值和实际意义。除了一致性问题外，近年来发展出一种扩展的一致性问题——分组一致性。与一致性不同的是，分组一致性是控制系统中的智能个体按子组收敛到不同的一致性值。在已有的文献中，一阶分组一致、二阶分组一致都有所研究。受以上分析启发，本文将研究一类由一阶智能体和二阶智能体组成的混合异质多智能体系统的分组一致性问题，将二阶智能体作为一个子组，一阶智能体作为一个子组，研究这两个子组存在信息耦合的情况下，控制各子组内部状态渐近地实现一致，具体只考虑系统离散时的分组一致性问题。

因此，需要一种针对一类混合异质多智能体系统的分组一致性控制方法以解决上述问题。

技术实现要素：

本发明针对现有技术的缺陷，提供一种针对一类混合异质多智能体系统的分组一致性控制方法。

为解决上述技术问题，本发明的针对一类混合异质多智能体系统的分组一致性控制方法所采用的技术方案为：

一种针对一类混合异质多智能体系统的分组一致性控制方法，包括以下步骤：

步骤一、分析由一阶智能体和二阶智能体组成的混合异质系统，得到混合异质系统在离散情况下的分组一致性；

步骤二、根据线性控制协议，运用代数图论、稳定性理论和矩阵理论，分析协议作用下闭环系统的系统矩阵及动态特性，得到系统渐近实现分组一致性的充分条件。

更进一步的，步骤一中考虑n个智能体组成的混合异质系统，其中，包括m个为二阶智能体，2≤m<n，n-m个为一阶智能体，n-m≥2。

更进一步的，设前m个为二阶智能体，智能体的索引属于集合i1＝{1,2,…,m}，后n-m个为一阶智能体，智能体的索引属于集合i2＝{m+1,…,n}，并记i＝i1∪i2，

二阶智能体为：

其中：xi(k)、vi(k)和ui(k)分别是第i∈i1个智能体在kt时刻的位置量、速度量和控制量，k∈n，t＞0为采样周期；

一阶智能体为：

xi(k+1)＝xi(k)+tui(k),i∈i2

其中，xi(k)和ui(k)分别是第i∈i2个智能体在kt时刻的位置量和控制量，k∈n，t＞0为采样周期。

更进一步的，步骤一中二阶智能体和一阶智能体的限制条件为满足下式：

更进一步的，步骤二中：

二阶智能体的分组一致性协议为：

一阶智能体分组一致性协议为：

式中，α≠0为控制增益，其中，ni1＝{vj|(vi,vj)∈e,j∈i1}和ni2＝{vj|(vi,vj)∈e,j∈i2}表示智能体i∈i的二阶智能体邻居集合和一阶智能体邻居集合，其中，ni＝ni1∪ni2。

更进一步的，如果α、t满足以下两个条件之一：

(1)re(λi)＞0且

(2)re(λi)＜0且

其中，λi为矩阵v的特征值，i＝3,4,…,n+m，α≠0为控制增益，t＞0为采样周期，u＝in+m-αtv，μi、λi分别是矩阵u和v的特征值，则有μi＝1-αtλi，其中i＝1,2,…,n+m，l11m＝0m，l21n-m＝0m，l31m＝0n-m，l41n-m＝0n-m；

则矩阵u仅有两个单的特征值1，且其余特征值均在复平面上的单位圆内。

更进一步的，如果α、t满足以下两个条件之一：

(1)re(λi)＞0且

(2)re(λi)＜0且

其中，λi为矩阵v的特征值，i＝3,4,…,n+m，α≠0为控制增益，t＞0为采样周期，

u＝in+m-αtv，μi、λi分别是矩阵u和v的特征值，则有μi＝1-αtλi，其中i＝1,2,…,n+m，l11m＝0m，l21n-m＝0m，l31m＝0n-m，l41n-m＝0n-m；

则二阶智能体和一阶智能体在二阶智能体的分组一致性协议和一阶智能体分组一致性协议作用下渐近实现分组一致。

有益效果：本发明的针对一类混合异质多智能体系统的分组一致性控制方法提出一类混合异质多智能体系统的分组一致性控制，更加符合实际工程实践的需要，更加贴近现实应用；考虑将多智能体系统分为两组在离散时间的情况下的渐近分组一致性，不失一般性。

附图说明

图1是针对一类混合异质多智能体系统的分组一致性控制方法的流程图；

图2是智能体位置曲线；

图3是智二阶能体速度曲线；

图4是智二阶能体加速度曲线

图1中：1为分析离散异质多智能体系统分组一致性，2为得出系统渐近实现分组一致性的充分条件，3为通过仿真实例对所得分析结果进行验证。

具体实施方式

下面结合附图和具体实施例，进一步阐明本发明，应理解这些实施例仅用于说明本发明而不用于限制本发明的范围，在阅读了本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。

本发明是一种针对一类混合异质多智能体系统的分组一致性控制方法，包括以下步骤：

步骤一、具体分析由一阶智能体和二阶智能体组成的混合异质系统，研究其在离散情况下的分组一致性；

步骤二、基于两个合理的假设提出了线性控制协议，运用代数图论、稳定性理论和矩阵理论，分析协议作用下闭环系统的系统矩阵及动态特性，取得了系统渐近实现分组一致性的充分条件；

步骤三、通过仿真实例对所得分析结果进行验证，验证本发明提到的方法的有效性。

进一步，步骤一中，考虑n个智能体组成的混合异质网络系统，其中m(2≤m<n)个为二阶智能体，n-m(n-m≥2)个为一阶智能体。不失一般性，假设前m个为二阶智能体，智能体的索引属于集合i1＝{1,2,…,m}，后n-m个为一阶智能体，智能体的索引属于集合i2＝{m+1,…,n}，并记i＝i1∪i2。

系统中二阶智能体为：

其中：xi(k)∈r^l、vi(k)∈r^l和ui(k)∈r^l。分别是第i∈i1个智能体在kt，k∈n时刻的位置量、速度量和控制量，t＞0为采样周期。

系统中一阶智能体为：

xi(k+1)＝xi(k)+tui(k),i∈i2(2)

其中xi(k)∈r^l和ui(k)∈r^l分别是第i∈i2个智能体在kt，k∈n时刻的位置量和控制量，t＞0为采样周期。

本发明的目标就是设计合适的控制协议ui(k)，i∈i，使得对于系统(1)和(2)的任何初始条件，满足：

和

则称系统(1)和(2)实现渐近分组一致。

进一步，步骤二中，。用g＝(v,e,a)表示含有n个节点的加权有向图，其节点集用v＝{vi:i＝1,2,…,n}表示，有向边集用表示，加权邻接矩阵用a＝[aij]∈r^n×n表示，节点下标为有限集in＝{1,2,…,n}。记eij＝(vi,vj)是有向图g中从父节点vj，到子节点vi的有向边，与边eij相关的aij称为边的权值，且规定aij＞0当且仅当eij∈e，否则aij＝0。ni＝{vj∈v:eij∈e}为顶点vi的邻居集。

图g的拉普拉斯矩阵定义为l＝λ-α∈r^n×n，其中λ＝diag{λ11,λ22,…,λnn}为对角阵，为节点vi的人度，α为图g的邻接矩阵。显然有l1n＝0n。

使用加权有向图g描述异质智能体组成的网络拓扑结构，有向图中的各个节点对应于拓扑结构中的各个智能体，有向图中的有向边表示智能体之间的信息交互，如果有一条从节点vj到节点vi有向边，则表示节点vi对应的智能体能接收到节点vj对应的智能体发送的信息，需要注意的是这里有向边的权值满足：

记ni1＝{vj|(vi,vj)∈e,j∈i1}、ni2＝{vj|(vi,vj)∈e,j∈i2}表示智能体i∈i的二阶智能体邻居集合和一阶智能体邻居集合，显然ni＝ni1∪ni2。利用智能体i自身及其邻居的状态信息设计分布式的分组一致性协议。在这里总是假定l＝1。

在分析之前，给出两个假定。

假定1：且

假定2：除两个单的零特征值外，图g对应的拉普拉斯矩阵l的特征值都具有正实部。

为二阶智能体设计如下分组一致性协议：

为一阶智能体设计如下分组一致性协议：

式(5)和(6)中，α≠0为控制增益。

将协议(5)和(6)应用到系统(1)和(2)中，得：

和

令结合式(7)并整理得：

记xs(k)＝[x1(k),…,xm(k)]^t，y(k)＝[y1(k),…,ym(k)]^t，xf(k)＝[xm+1(k),…,xn(k)]^t结合式(8)和(9)得：

和

xf(k+1)＝-αtl3xs(k)+(in-m-αtl4)xf(k)(11)

式(10)和(11)中l1∈r^m×m、l2∈r^m×(n-m)、l3∈r^(n-m)×m、l4∈r^(n-m)×(n-m)满足

记z(k)＝[xs^t(k),y^t(k),xf^t(k)]^t，将式(10)和式(11)写成紧凑形式得：

z(k+1)＝uz(k)(12)

式中

将系统(12)的系统矩阵u写成：

u＝in+m-αtv

式中：

设μi、λi分别是矩阵u和v的特征值，则有μi＝1-αtλi，其中i＝1,2,…,n+m。

令可以验证这里利用了l11m＝0m，l21n-m＝0m，l31m＝0n-m，l41n-m＝0n-m，因此，0是矩阵v的特征值，其代数重数至少为2，是矩阵v与0对应的右特征向量。

对分块矩阵v进行简单的初等变换可得：

可以看出rank(v)＝m+rank(l)＝n+m-2，因此，v的特征值零，其代数重数和几何重数均为2，这里记λ1＝λ2＝0。

如果α、t满足以下两个条件之一：(1)re(λi)＞0且re(λi)＜0且其中，λi为矩阵v的特征值，i＝3,4,…,n+m，则矩阵u仅有两个单的特征值1，且其余特征值均在复平面上的单位圆内。

如果α、t满足以下两个条件之一：(1)re(λi)＞0且re(λi)＜0且其中，λi为矩阵v的特征值，i＝3,4,…,n+m，则系统(1)和(2)在协议(5)和(6)作用下渐近实现分组一致。

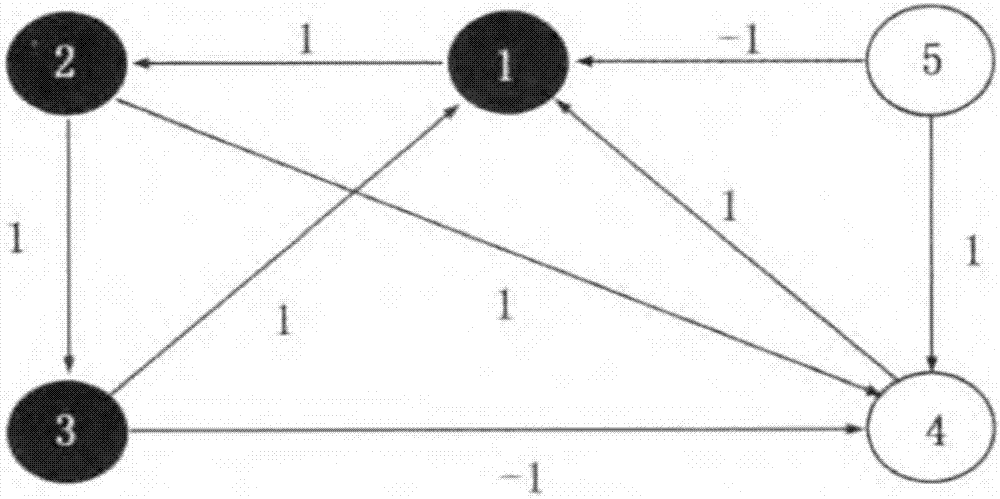
进一步，步骤三中，考虑由5个智能体组成的离散混合异质多智能体系统，系统交互拓扑图如图2所示，其中黑色圆盘表示二阶智能体，白色圆盘表示一阶智能体。智能体之间的邻接权值在图2中已经标出，满足假定1。图2对应的拉普拉斯矩阵l的特征值也满足假定2。矩阵v的特征值为0、0、0.5698、1、0.2151±1.3071i、1±i。将v的非零特征值代入计算可得设采样周期t＝0.2s，根据控制协议对控制增益的要求，取α＝0.6，取系统初始状态为xs(0)＝[2,1,-1]^t，vs(0)＝[-1,1,0.5]^t，xf(0)＝[-1,1]^t。在协议(5)和(6)的作用下，系统中各智能体的状态变化如图3、图4所示，从图中可看出，系统渐近地实现了状态分组一致，验证了本发明中设计的控制协议的有效性。