基于中立模型的钻柱系统的粘滑振动抑制方法及系统与流程

本发明涉及资源开发的钻进系统领域，更具体地说，涉及一种基于中立模型的钻柱系统的粘滑振动抑制方法及系统。

背景技术：

当今时代，资源能源是人类社会赖以生存和发展的物质基础，以石油为主的三大能源物质不仅为全人类提供能源，同时也作为重要的化工原料服务于社会。由此可见，资源能源在当代社会中占据着不可替代的地位。立足于国情，我国传统重要矿产资源查明程度平均为30.3％，矿产资源勘探深度平均只有500m，油气开采深度平均也不足4500m。按照矿产资源勘探深度500m以上、油气开采深度4500m以上来界定深部钻探，我国深层石油资源与天然气资源分别占剩余石油资源与剩余天然气资源的40％和60％左右；同时我国的非常规能源如页岩气、煤层气、地热等储量丰富。因此，随着浅层资源的日益枯竭以及常规能源的开发难以满足需求，深部勘探和非常规资源能源的开发成为必然。

然而在钻进过程中，由于钻进系统受到摩擦、信息传播时延、非线性阻尼等不同因素的影响，使得钻柱产生轴向、横向以及扭矩方向的振动。在这些振动中，粘滑振动存在于50％以上的钻进时间，是最为广泛、危害性最大的一类。因此，进行钻柱粘滑振动的研究，对于保持钻进过程的稳定、提高钻进的效率、提升钻进的安全等都有很大的安全与经济意义。

技术实现要素：

本发明要解决的技术问题在于，针对上述的现有技术中粘滑振动对钻进系统存在影响的技术缺陷，提供了一种基于中立模型的钻柱系统的粘滑振动抑制方法及系统。

根据本发明的其中一方面，本发明为解决其技术问题，提供了一种基于中立模型的钻柱系统的粘滑振动抑制方法，包括以下步骤：

s1、基于钻柱系统的微单元的动力学模型，使用偏微分方程对钻柱系统进行建模，得到钻柱系统的分布参数模型以及分布参数模型的边界条件；

s2、结合所述边界条件，使用达朗贝尔法求解所述分布参数模型，得到中立时滞微分方程；

s3、基于所述中立时滞微分方程，通过构造钻柱系统模型、状态观测器、干扰估计器、状态反馈以及内模，以形成粘滑振动抑制控制系统；其中，在构造过程中，通过构建状态观测器观测钻柱系统状态，结合低通滤波器来进行干扰估计器的扰动估计，并将估计的信号作用在输入端，同时结合状态反馈和内模实现对给定输入的跟踪；

s4、使用状态空间方程对该粘滑振动抑制控制系统进行描述，得到标准的时滞系统，接着构造李雅普诺夫泛函，给出线性矩阵不等式形式的系统稳定性判据，求解线性矩阵不等式的可行性问题，得到振动抑制控制系统的设计参数，根据具有所述设计参数的粘滑振动抑制控制系统来控制钻柱系统的运行。

优选的，在上述的粘滑振动抑制方法的步骤s1中：

钻柱系统的分布参数模型通过下述方法得到：将钻柱考虑成由无限多的具有转动惯量和扭转刚度的微小单元组成的系统，考虑钻柱上任意质点在任意时刻的位移，使用偏微分方程描述钻柱系统，得到钻柱系统分布参数模型；

所述边界条件包括顶部边界条件以及底部边界条件；

顶部边界条件通过下述方法确定：对于钻柱顶部，转盘驱动电机的输出转速往往与顶部钻柱的转速难以完全相同，这种速度差异会导致钻柱顶部的产生扭转力，由此确定顶部边界条件；

底部边界条件通过下述方法确定：对于底部，顶部的扭转波传递到底部，驱动钻头的运动，同时克服非线性的钻头-岩石作用率，由此确定底部边界条件。

优选的，在上述的粘滑振动抑制方法中，步骤s2具体包括以下过程：

s21、去掉分布参数模型中伴随着钻柱的阻尼，从而得到标准的波动方程：

s22、将标准的波动方程进行变量的变换，通过达朗贝尔法求解变换后的标准波动方程的通解，再结合边界条件，得到含有输入时滞的中立时滞模型；

s23、去掉其输入时滞，得到只含有状态时滞的中立时滞模型作为所述中立时滞微分方程。

优选的，在上述的粘滑振动抑制方法中，步骤s3具体包括以下过程：

s31、基于所述中立时滞微分方程，构造以状态空间方程描述的钻柱系统模型与状态观测器模型；

s32、使用状态观测器来观测钻柱系统模型状态，结合低通滤波器来进行扰动估计，并将估计的信号作用在输入端，以完成等价干扰的输入；

s33、结合状态反馈和内模实现对给定输入的跟踪。

优选的，在上述的粘滑振动抑制方法中，步骤s4具体包括以下过程：

s41、根据选取的状态变量，使用状态空间方程重构所述中立时滞微分方程，得到时滞系统的标准化模型；

s42、基于所述标准化模型，构造合适的李雅普诺夫泛函，通过对泛函求导以及变换得到以线性矩阵不等式形式描述的系统稳定性判据，同时推导出状态反馈系数与观测器增益；

s43、求解线性矩阵不等式的可行性问题，得到振动抑制控制系统设计参数。

根据本发明的另一方面，本发明为解决其技术问题，还提供了一种基于中立模型的钻柱系统的粘滑振动抑制系统，包括：

分布参数模型获取单元，用于基于钻柱系统的微单元的动力学模型，使用偏微分方程对钻柱系统进行建模，得到钻柱系统的分布参数模型以及分布参数模型的边界条件；

中立时滞微分方程求解单元：结合所述边界条件，使用达朗贝尔法求解所述分布参数模型，得到中立时滞微分方程；

粘滑振动抑制控制系统形成单元，用于所述中立时滞微分方程，通过构造钻柱系统模型、状态观测器、干扰估计器、状态反馈以及内模，以形成粘滑振动抑制控制系统；其中，在构造过程中，通过构建状态观测器观测钻柱系统状态，结合低通滤波器来进行干扰估计器的扰动估计，并将估计的信号作用在输入端，同时结合状态反馈和内模实现对给定输入的跟踪；

设计参数求解及控制单元，用于状态空间方程对该粘滑振动抑制控制系统进行描述，得到标准的时滞系统，接着构造李雅普诺夫泛函，给出线性矩阵不等式形式的系统稳定性判据，求解线性矩阵不等式的可行性问题，得到振动抑制控制系统的设计参数，根据具有所述设计参数的粘滑振动抑制控制系统来控制钻柱系统的运行。

优选的，在上述的粘滑振动抑制方法的分布参数模型获取单元中：

钻柱系统的分布参数模型通过下述方法得到：将钻柱考虑成由无限多的具有转动惯量和扭转刚度的微小单元组成的系统，考虑钻柱上任意质点在任意时刻的位移，使用偏微分方程描述钻柱系统，得到钻柱系统分布参数模型；

所述边界条件包括顶部边界条件以及底部边界条件；

顶部边界条件通过下述方法确定：对于钻柱顶部，转盘驱动电机的输出转速往往与顶部钻柱的转速难以完全相同，这种速度差异会导致钻柱顶部的产生扭转力，由此确定顶部边界条件；

底部边界条件通过下述方法确定：对于底部，顶部的扭转波传递到底部，驱动钻头的运动，同时克服非线性的钻头-岩石作用率，由此确定底部边界条件。

优选的，在上述的粘滑振动抑制方法中，中立时滞微分方程求解单元具体包括：

阻尼去除子单元，用于去掉分布参数模型中伴随着钻柱的阻尼，从而得到标准的波动方程：

达朗贝尔法求解子单元，用于将标准的波动方程进行变量的变换，通过达朗贝尔法求解变换后的标准波动方程的通解，再结合边界条件，得到含有输入时滞的中立时滞模型；

输入时滞去除子单元，用于去掉其输入时滞，得到只含有状态时滞的中立时滞模型作为所述中立时滞微分方程。

优选的，在上述的粘滑振动抑制方法中，粘滑振动抑制控制系统形成单元具体包括：

模型构造子单元，用于基于所述中立时滞微分方程，构造以状态空间方程描述的钻柱系统模型与状态观测器模型；

观测及扰动子单元，用于使用状态观测器来观测钻柱系统模型状态，结合低通滤波器来进行扰动估计，并将估计的信号作用在输入端，以完成等价干扰的输入；

输入跟踪子单元，用于结合状态反馈和内模实现对给定输入的跟踪。

优选的，在上述的粘滑振动抑制方法中，设计参数求解及控制单元具体包括：

中立时滞微分方程重构子单元，用于根据选取的状态变量，使用状态空间方程重构所述中立时滞微分方程，得到时滞系统的标准化模型；

变换推导子单元，用于基于所述标准化模型，构造合适的李雅普诺夫泛函，通过对泛函求导以及变换得到以线性矩阵不等式形式描述的系统稳定性判据，同时推导出状态反馈系数与观测器增益；

设计参数求解子单元，用于求解线性矩阵不等式的可行性问题，得到振动抑制控制系统设计参数。

本发明提出了一种基于中立模型的钻柱系统的粘滑振动抑制方法及系统，针对分布参数模型描述的钻柱系统进行简化，得到中立时滞模型，在此基础上构造了基于等价输入干扰方法的粘滑振动抑制控制系统，建立控制系统的标准化状态空间方程模型，紧接着构造合适的李雅普诺夫泛函，给出线性矩阵不等式形式的系统稳定性判据；通过求解解线性矩阵不等式的可行性问题，得到振动抑制控制系统设计参数，最后来抑制粘滑振动。本发明不需要考虑具体的扰动模型，只需对扰动进行估计，从而快速消除扰动带来的影响，特别对于深部钻探下的复杂地层环境，存在着钻头-岩石作用率不明确甚至不可知的实际情况，仍能起到很好的扰动抑制效果。而且该粘滑振动抑制控制系统的构造简单明了，只需设计3个参数即可完成对扰动的抑制。

附图说明

下面将结合附图及实施例对本发明作进一步说明，附图中：

图1为本发明的基于中立模型的钻柱系统的粘滑振动抑制系统的总体结构框图；

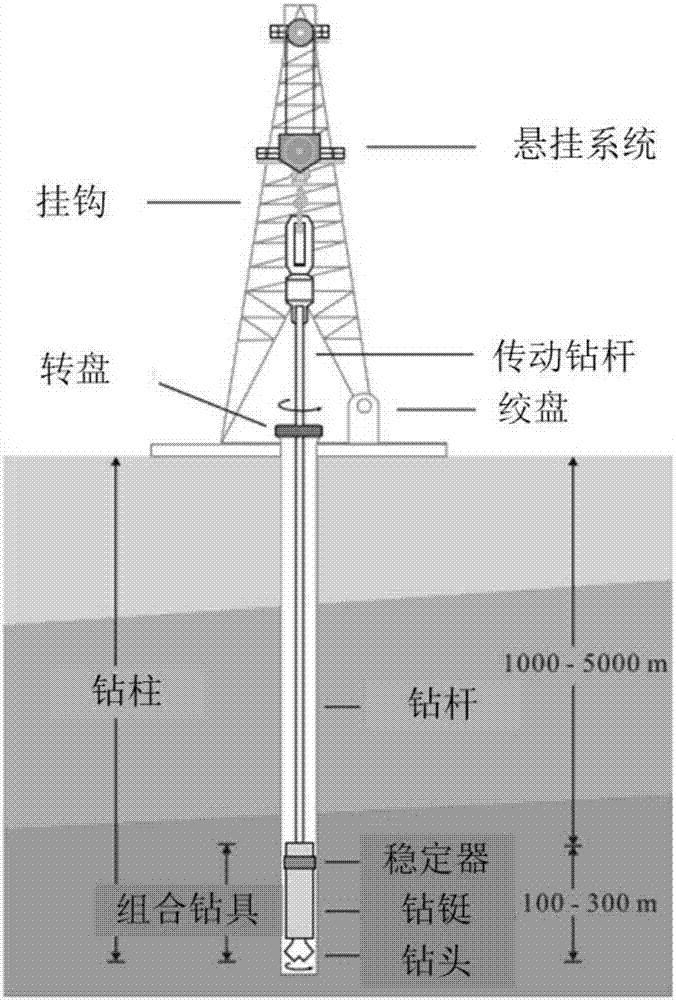
图2为本发明的钻进系统结构图；

图3为本发明的钻柱扭转振动微元图；

图4(a)、4(b)分别为本发明的粘滑振动的底部钻头转速的仿真图以及钻头上的力矩仿真图；

图5为本发明的钻柱系统结构框图；

图6为本发明的状态观测器结构图；

图7(a)、(b)分别为本发明的粘滑振动抑制系统控制下钻柱钻头响应以及钻头转速局部放大图；

图8为本发明的剧烈扰动下的基于中立模型的钻柱系统粘滑振动抑制系统控制的钻柱钻头响应。

具体实施方式

为了对本发明的技术特征、目的和效果有更加清楚的理解，现对照附图详细说明本发明的具体实施方式。

本发明提供了一种基于中立模型的钻柱系统粘滑振动抑制系统，其总体结构框图如图1所示，该抑制系统可工作于图2所示的钻进系统中。本发明首先分析钻柱系统的动力学得到分布参数模型，接着对其简化得到波动方程，并使用达朗贝尔法求解、变换得到中立时滞模型；然后构建状态观测器观测被控系统状态，结合低通滤波器来进行扰动估计，同时结合状态反馈和内模实现对给定输入的跟踪，完成基于等价输入干扰方法的粘滑振动抑制控制系统；最后使用状态空间方程对该控制系统进行描述，得到标准的时滞系统，接着构造合适的李雅普诺夫泛函，给出线性矩阵不等式形式的系统稳定性判据；从而使用matlab的lmi工具箱求解线性矩阵不等式的可行性问题，得到振动抑制控制系统设计参数。该方法不需要考虑具体的扰动模型，只需对扰动进行估计，从而快速消除扰动带来的影响，特别对于深部钻探下的复杂地层环境，存在着钻头-岩石作用力不明确甚至不可知的实际情况，该方法对于其所导致的粘滑振动现象仍能起到很好的扰动抑制效果。

控制系统的搭建和振动抑制控制系统参数设计的具体步骤如下：

步骤1：建立分布参数模型以及其边界条件。

(1)建立分布参数模型。针对钻柱的扭转振动，建立钻柱扭转振动微元图。考虑钻柱的长度为l，密度为ρ。f(x,t)表示单位长度杆上分布的外力偶矩，θ(x,t)为杆上距离原点x处的截面在t时刻的角位移，p为截面处的扭矩，ρjdx表示微单元绕轴线的转动惯量。

设钻柱截面的二次极矩为j，剪切模量为g，由达朗贝尔原理以及材料力学得到钻柱分布参数模型：

这里表示扭转波的纵向传递速度。

(2)建立分布参数模型边界条件。

1)确定顶部边界条件。对于实际情况，转盘驱动电机的输出转速往往与顶部钻柱的转速难以完全相同，这种速度差异会导致钻柱顶部的产生扭转力，考虑这种现象，有以下边界条件：

其中表示钻柱顶部的扭矩，β表示角动量，表示钻柱顶部转速，ω(t)表示输入转速。

2)确定底部边界条件。钻柱的底部情况是，顶部的扭转波传递到底部，驱动钻头的运动，同时克服非线性的钻头-岩石作用率。边界条件如下：

其中ib表示底部组合钻具的转动惯量，为钻柱底部的扭矩，和分别表示钻头的角速度及角加速度，t(·)表示钻头-岩石作用率。

步骤2：进行分布参数模型的简化，得到中立时滞模型

对于钻柱系统分布参数模型(1)忽略其系统阻尼后，变为波动方程：

引进变量γ＝t+cx，η＝t-cx。由达朗贝尔法知，式(4)的通解为：

其中和ψ是任意连续可微的实值函数，分别代表任意的上行波和下行波。

将底部钻头转速定义为

结合波动方程通解，边界条件(2)、(3)以及(6)，经过推导与变换，得到使用中立时滞微分方程描述的钻柱系统：

其中，τ＝cl。

由式(7)知，该中立时滞系统包含输入时滞，在不影响对粘滑振动的仿真与分析的情况下，为了简化系统，忽略掉式(7)输入时滞，得到：

由此，建立了以中立时滞微分方程描述的中立时滞模型，该模型只含有状态时滞而不含有输入时滞。

步骤3：构造基于等价输入干扰方法的粘滑振动抑制控制系统。

粘滑振动抑制控制系统包含5个部分，分别是钻柱系统模型、状态观测器、干扰估计器、状态反馈以及内模。

(1)确定钻柱系统模型。首先将(8)以状态空间方程进行描述，根据eid(equivalentinputdisturbance，等价输入干扰)的思想，将其转化为：

其中，de(t)是干扰输入信号d(t)的等价输入干扰。

(2)建立状态观测器。选用全维观测器，其结构图如图6所示，其状态空间方程为：

其中是状态x(t)的观测状态，矩阵l是待定的增益矩阵，y为钻头转速。

(3)建立扰动估计器。使用状态观测器观测系统状态，结合低通滤波器来进行扰动估计。

1)滤波器f(s)的状态空间方程为：

其中，xf(t)为滤波器状态，为滤波后的扰动信号。其传递函数f(s)满足：

其中，ωr为所选的扰动估计最高角频率。而适合的滤波器切换角频率通常大于ωr的10倍。

2)确定扰动估计值。图1的扰动估计值为：

其中，b⁺＝b^t(b^tb)^-1。

(4)确定内部模型

由图1知，内部模型为：

用来保证对顶部参考输入的精确跟踪。当参考输入已知时，参数ar和br可以直接确定。

基于以上4个步骤，此时，控制率设计为：

uf(t)＝krxr(t)+r′(t)(15)

式中，krxr(t)为状态反馈，即为图1中所述图kp。

因此，基于eid的闭环系统控制输入为：

步骤4：控制系统稳定性判据和振动抑制控制系统参数设计

(1)时滞系统的模型标准化

令

r(t)＝0,r′(t)＝0,d(t)＝0(17)

选用

来描述闭环系统。得到以下表达式：

综上所述，可得闭环控制系统的状态空间表达式：

其中

(2)时滞稳定性条件

对于中立时滞系统(22)在控制率(15)的作用下是渐进稳定的，如果存在正定矩阵yj(j＝1,2,3)，mj(j＝1,2,3)，x1、x2、x11、x22和x3及合适维数的矩阵w1、w2，使得如下lmi可行：

其中

φ33＝(af+bfcf)x3+x3(af+bfcf)^t，

ψ15＝diag{x1,x2,x3}，

ψ22＝diag{y1,y2,y3}，

ψ33＝ψ44＝diag{m1,m2,m3}，

ψ55＝diag{y1,y2,y3}。

且x2的奇异值分解为：

x2＝vdiag{x11,x22}v^t(24)

矩阵c的奇异值分解为

c＝u[s,0]v^t(25)

(3)振动抑制控制系统参数设计

1)：对于扰动估计的最高角频率，选择滤波器时间常数t＝1/(10ωr)，而且一阶低通滤波器可以满足扰动估计需求，据此，选择合适的的滤波器参数af，bf和cf；

2)：利用matlab的lmi工具箱求解式(23)的可行解，计算振动抑制控制系统增益kp和l：

3)：根据已知的阶跃参考输入，选择内模参数

ar＝0(27)

通过调节br，以达到最优的控制效果。

本发明应用以上步骤，完成了基于等价输入干扰方法的粘滑振动抑制控制系统设计。

针对在钻压wob＝45000n，钻柱长度l＝1172m，钻井液阻尼cb＝0.03nmsrad^-1，参考转速ω＝6rad/s下的钻柱粘滑振动进行抑制控制，得到如图7所示的仿真结果。

与图4的a图和b图的粘滑振动现象相对比，仿真验证了基于eid控制系统的有效性。系统在4次振荡后逐渐进入稳态。

从经典控制理论的角度分析，以调节时间为系统到达并保持在终值±2％内所需的最短时间为标准，由于系统的终值为6rad/s，因此，其±2％的范围即为5.88rad/s～6.12rad/s。通过在仿真图中绘制5.88和6.12两条曲线，可以发现基于eid的控制使得钻柱系统在t＝12.93s时进入稳态。

更多的，为了评判该控制系统的扰动抑制能力，分别测试在钻压wob＝60000n、钻柱长度l＝2000m以及顶部参考转速ω＝6rad/s下不加振动抑制控制系统和加上振动抑制控制系统钻柱系统的响应。

观察图8的a图可知，此时钻柱发生剧烈的粘滑振动，粘滞期与滑动期变宽，对钻柱损伤巨大。观察图8的b图知，加入eid控制策略之后，系统在t＝20.45s进入稳态，可见控制的有效性。

上面结合附图对本发明的实施例进行了描述，但是本发明并不局限于上述的具体实施方式，上述的具体实施方式仅仅是示意性的，而不是限制性的，本领域的普通技术人员在本发明的启示下，在不脱离本发明宗旨和权利要求所保护的范围情况下，还可做出很多形式，这些均属于本发明的保护之内。