用于互联电网自动发电控制的可变域MPC方法与流程

本发明涉及一种用于互联电网自动发电控制(agc)的可变域mpc方法，通过引入阈值构成控制域变换条件，根据控制状态优劣进行mpc控制器的控制域变换，即根据不同的控制需求与控制效果进行不同控制域的切换，以满足不同环境下agc的控制精度要求，从而提升算法实际运用价值，实现互联电网agc系统的灵活控制，属于agc控制技术领域。

背景技术：

近年来，随着互联电网规模的不断扩大，负荷变化形式越来越复杂，如何优化agc系统控制方法也成为一个值得研究的课题。目前针对此问题出现了多种控制方法：基于遗传模糊pid的液压agc控制系统研究、基于无模型自适应控制算法的互联电网agc、基于时滞模型预测控制算法的网络化agc研究。基于遗传模糊pid的agc控制系统能克服传统模糊控制需人为设定隶属度且不能动态调整参数的弊端；基于无模型自适应控制算法的互联电网agc系统具有较强的鲁棒性、非线性适应性及cps指标；基于时滞模型预测控制算法的网络化agc控制系统确保了网络化agc对通信延迟的鲁棒性和适应性。上述列举控制方法虽然能够保证控制系统的稳定性和动态性能，但普遍存在控制精度单调，控制算法复杂的问题，而实际控制过程中，互联电网agc有各种不同的控制精度和效果需求。因此，针对不同控制需求的控制方法更具实际意义。

鉴于mpc不仅能提升对具有时滞性、非线性和不确定性特征系统控制的鲁棒性，还能实现控制量实时在线优化和控制域的灵活改变。所以，模型预测控制算法对于agc系统不同控制需求的处理有很大的参考意义。

模型预测控制(modelpredictivecontrol,mpc)技术从上世纪70年代问世以来,已经从最初在工业过程中应用的启发式控制算法发展成为一个具有丰富理论和实践内容的新的学科分支。预测控制针对的是有优化需求的控制问题,30多年来预测控制在复杂工业过程中所取得的成功,已充分显现出其处理复杂约束优化控制问题的巨大潜力。进入本世纪以来,随着科学技术的进步和人类社会的发展,人们对控制提出了越来越高的要求,不再满足于传统的整定设计,而希望控制系统能通过优化获得更好的性能。同时,优化受到了更多因素的制约,除了传统执行机构等物理条件的约束外,还要考虑各种工艺性、安全性、经济性(质量、能耗等)和社会性(环保、城市治理等)指标的约束,这两方面的因素对复杂系统的约束优化控制提出了新的挑战。

模型预测控制是一种基于模型的闭环优化控制算法，其算法的核心是：可预测未来的动态模型，在线反复优化计算并滚动实施的控制作用和模型误差的反馈校正。模型预测控制具有控制效果好、鲁棒性强等优点，可有效地克服过程的不确定性、非线性和并联性，并能方便的处理过程被控变量和操纵变量中的各种约束。

模型预测控制算法是一种滚动的优化算法：在每一时刻以系统的当前状态为初始状态，通过在线求解一个有限时域的优化问题而得到一个控制序列，并将该序列的第一项作为输入应用到系统中，在下一个采样时刻，重复上述过程。

在agc的实际控制过程中，特别是在涉及区域较大较多的互联电网系统中，在应对环境复杂、控制要求多样化时，传统模型预测控制算法(mpc)的固定控制域模式无法满足多元化控制要求。所以需要提出一种处理方法来满足复杂环境下agc的多元化控制需求。

技术实现要素：

本发明的目的是：提供一种用于互联电网自动发电控制(agc)的可变域mpc控制方法，通过引入阈值构成控制域变换条件，根据控制状态优劣进行mpc控制器的控制域变换，以满足不同复杂环境下agc的多元化控制精度要求，从而提升算法实际运用价值，实现互联电网agc系统的灵活控制。

为了达到上述目的，本发明所采用的技术方案是：用于互联电网自动发电控制的可变域mpc方法，其特征在于，所述方法包括如下步骤：

(1)对于具备两种域大小的可变域状态，首先设置一个阈值ε；

(2)然后采样系统的输出δfi；

(3)最后在每次采样计算过程中，根据系统的输出δfi进行控制域变换条件判断：

当δfi大于阈值ε时，mpc控制器会切换到较大控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象；

当δfi小于或等于阈值ε时，mpc控制器会切换到较小控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象。

进一步地，所述方法具体实现过程包括：

步骤1：模型预测控制系统的分析是基于研究对象的数学模型，假设以离散形式描述的研究对象数学模型如下所示：

x(k+1)＝ax(k)+bu(k)+fw(k)

y＝cx(k)

其中，x为状态变量，u为状态变量，w为状态变量，y为状态变量，a为系统矩阵，b为输入矩阵，c为输出矩阵，f为扰动矩阵，k为采样时刻，目标函数定义为：

j＝(rs-y)^t(rs-y)

其中，rs是输出的期望值，y是输出量的预测序列，其控制过程表现为针对目标函数的优化，在每一采样时刻系统都会计算出一个最优的输入序列：

u^*＝[u^*(k)u^*(k+1)…u^*(k+nc-1)]^t

其中，nc为系统的控制域，传统mpc控制过程中，系统只将输入序列第一个元素u^*(k)作用于对象；

步骤2：检测系统的输出δfi并进行控制域变换条件判断：

其中δfi为系统可测输出，u(k)为控制变量，u2(ki+1)为控制域较大时mpc控制器所计算最优序列的第一个元素，u1(ki+1)为控制域较小时mpc控制器所计算最优序列的第一个元素；

当δfi大于阈值ε时，mpc控制器会切换到较大控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象；当δfi小于或等于阈值ε时，mpc控制器会切换到较小控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象。

进一步地，步骤2中，具体实现过程包括：

step1：当δfi>ε时，转到step2；当δfi≤ε时，转到step3；

step2：采用mpc控制器较大控制域在线优化；

step3：采用mpc控制器较小控制域在线优化；

step4：将控制作用的第一个作用实施到对象；

step5：在下一采样时刻，转到step1。

与现有技术相比，本发明的有益效果是：本发明采用可变域的模型预测控制(mpc)控制方式，提高了算法的实际运用价值，实现了互联电网agc系统的灵活控制。

附图说明

图1两区域互联电网agc系统动态模型；

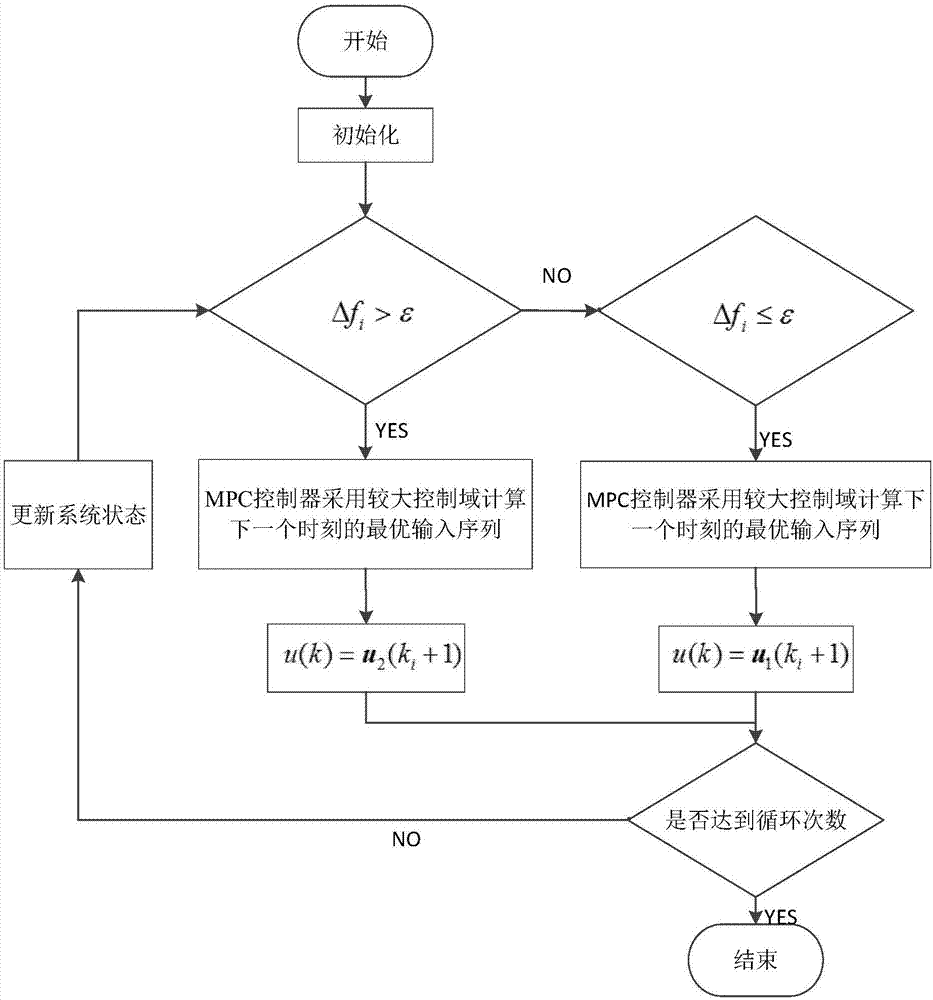
图2可变域的模型预测控制流程图；

图3可变域的mpc原理图；

图4阶跃信号下ace1响应曲线；

图5阶跃信号下ace2响应曲线；

图6阶跃信号下δf1响应曲线；

图7阶跃信号下δf2响应曲线。

具体实施方式

为了便于本领域普通技术人员理解和实施本发明，下面结合实施例对本发明作进一步的详细描述，应当理解，此处所描述的实施示例仅用于说明和解释本发明，并不用于限定本发明。

由于传统模型预测控制(mpc)算法的控制域是固定的，因此复杂环境下控制域固定的模式缺乏区分度和灵活性。本发明通过引入阈值构成控制域变换条件，根据控制状态优劣进行mpc控制器的控制域变换，即根据不同的控制需求与控制效果进行不同控制域的切换，以满足不同环境下agc的控制精度要求，从而提升算法实际运用价值，实现互联电网agc系统的灵活控制。

本发明的技术方案具体描述如下：一种用于互联电网自动发电控制的可变域mpc方法，以具备两种域大小的可变域状态为例，其特征在于：

①首先设置一个阈值ε；

②然后采样系统的输出δfi；

③最后在每次采样计算过程中，根据系统的输出δfi进行控制域变换条件判断：

当δfi大于阈值ε时，mpc控制器会切换到较大控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象；

当δfi小于或等于阈值ε时，mpc控制器会切换到较小控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象。

上述方法具体实现过程如下：

步骤1：模型预测控制系统的分析是基于研究对象的数学模型，假设以离散形式描述的研究对象数学模型如下所示：

x(k+1)＝ax(k)+bu(k)+fw(k)

y＝cx(k)

其中，x为状态变量，u为状态变量，w为状态变量，y为状态变量，a为系统矩阵，b为输入矩阵，c为输出矩阵，f为扰动矩阵，k为采样时刻。目标函数定义为：

j＝(rs-y)^t(rs-y)

其中，rs是输出的期望值，y是输出量的预测序列。其控制过程表现为针对目标函数的优化，在每一采样时刻系统都会计算出一个最优的输入序列：

u^*＝[u^*(k)u^*(k+1)…u^*(k+nc-1)]^t

其中nc为系统的控制域，传统mpc控制过程中，系统只将输入序列第一个元素u^*(k)作用于对象。

步骤2：检测系统的输出δfi并进行控制域变换条件判断：

其中δfi为系统可测输出，u(k)为控制变量，u2(ki+1)为控制域较大时mpc控制器所计算最优序列的第一个元素，u1(ki+1)为控制域较小时mpc控制器所计算最优序列的第一个元素。

当δfi大于阈值ε时，mpc控制器会切换到较大控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象；当δfi小于或等于阈值ε时，mpc控制器会切换到较小控制域计算出最优控制序列，并将序列的第一个元素作为控制信号作用于控制对象。具体如下：

step1：当δfi>ε时，转到step2；当δfi≤ε时，转到step3。

step2：采用mpc控制器较大控制域在线优化。

step3：采用mpc控制器较小控制域在线优化。

step4：将控制作用的第一个作用实施到对象。

step5：在下一采样时刻，转到step1。

可变域的模型预测控制流程框图如图2所示。

mpc的核心是可预测未来的动态模型，在线反复优化计算并滚动实施的控制作用和模型误差的反馈校正。模型预测控制具有控制效果好、鲁棒性强等优点，可有效地克服过程的不确定性、非线性和并联性，并能方便的处理过程被控变量和操纵变量中的各种约束。

原则上，控制器的控制域越大，系统输出响应超调量越小，控制效果越好，但时间复杂度越高。可变控制域的核心在于系统输出和控制域变换条件，当控制域变换条件成立时，系统自动选择相对应大小的控制域。

设计一个包含两种控制域的mpc控制器，一个控制域较小，另一个控制域较大。在控制过程中，当输出满足控制域变换条件1时，mpc控制器切换到较大的控制域进行未来控制与输出序列的计算，当输出满足控制域变换条件2时，mpc控制器切换到较小的控制域进行未来控制与输出序列的计算。

下面根据具体实施例对本发明进行说明。本发明选用的实验平台为两区域互联电网agc系统，其数学模型为：

yi(t)＝ciixi(t)

(i＝1,2；j＝1,2)

式中，xi∈rⁿ，ui∈r^m，wi∈r^k，yi∈r^r分别代表第i个区域系统状态变量、控制变量、扰动变量和输出变量。其中，

xi＝[δfiδptiδpriδxgiδpt12]^t

ui＝[δpci]wi＝[δpli]

yi＝[aceiδfiδpt12]^t

b12＝b21＝05×1f12＝f21＝05×1

根据上文的数学模型，利用matlab中模型预测控制的工具箱，构建出两区域互联电网agc系统的模型，如图1所示，在图1中，将ace1、ace2的期望值作为mpc控制器的输入，每一采样时刻，mpc控制器会计算出一个最优序列。

表1两区域互联agc系统动态模型仿真参数

将系统的输出δfi送至切换控制器中进行判断，当输出满足控制域变换条件1时，mpc控制器切换到较大控制域进行未来控制与输出序列的计算，当输出满足控制域变换条件2时，mpc控制器切换到较小控制域进行未来控制与输出序列的计算。基于可变域的模型预测控制原理图如图3所示。

为研究各种扰动情况下，采用本发明所提方法进行控制的agc系统的动态性能和稳定性，给定区域1的扰动负荷δpl1为0.06pu，区域2的扰动负荷δpl2为0.02pu，ε＝0.001，测试扰动输入为阶跃信号时agc系统的各输出响应，如图4～7所示。

从图4～7中可以看出，相比控制域固定的情况下，控制域可变时系统各输出响应的超调量更小，且控制域固定时，超调量随着控制域的增大而减小，系统最终均趋于稳定。该输出波形验证了本发明所提的用于互联电网自动发电控制(agc)的可变域mpc控制方法的可行性与有效性。

应当理解的是，本说明书未详细阐述的部分均属于现有技术。

应当理解的是，上述针对较佳实施例的描述较为详细，并不能因此而认为是对本发明专利保护范围的限制，本领域的普通技术人员在本发明的启示下，在不脱离本发明权利要求所保护的范围情况下，还可以做出替换或变形，均落入本发明的保护范围之内，本发明的请求保护范围应以所附权利要求为准。