高速无人飞行器的控制方法、装置和高速无人飞行器与流程

本发明涉及高速无人飞行器技术领域，尤其是涉及一种高速无人飞行器的控制方法、装置和高速无人飞行器。

背景技术：

高速无人飞行器具有飞行速度快、可靠高效等特点，有着巨大的军事价值和潜在的民用价值，受到了世界各国的普遍关注。但是高速无人飞行器存在非线性、强耦合和未建模动态等特性，这些不确定性将对高速无人飞行器的闭环控制系统的设计带来巨大挑战。

为了抑制不确定性对高速无人飞行器闭环控制系统的影响，可以采用基于自适应控制方法设计多个非线性控制器，以减少参数不确定性和非线性对闭环控制系统的影响；还可以利用平方和控制算法设计具有参数不确定性的高超声速飞行器模型的非线性动态控制器。但是，这些现有的控制方式难以抑制多种不确定性对高速无人飞行器的影响，导致控制误差较大。

技术实现要素：

有鉴于此，本发明的目的在于提供一种高速无人飞行器的控制方法、装置和高速无人飞行器，以抑制多种不确定性对飞行器控制的影响，减少飞行器控制方式的保守性，从而提高控制精确度。

第一方面，本发明实施例提供了一种高速无人飞行器的控制方法，包括：获取高速无人飞行器输出的状态量；所述状态量包括速度状态量和高度状态量；根据期望状态和所述状态量计算误差状态量；误差状态量包括速度误差状态量和高度误差状态量；对误差状态量进行线性二次调节处理，输出第一控制输入量；对误差状态量进行鲁棒补偿处理，输出第二控制输入量；采用反馈线性化方式，根据第一控制输入量和第二控制输入量生成最终控制输入量，通过最终控制输入量对高速无人飞行器进行控制。

第二方面，本发明实施例提供了一种高速无人飞行器的控制装置，包括：状态量获取模块，用于获取高速无人飞行器输出的状态量；所述状态量包括速度状态量和高度状态量；误差状态量计算模块，用于根据期望状态和所述状态量计算误差状态量；误差状态量包括速度误差状态量和高度误差状态量；二次调节处理模块，用于对误差状态量进行线性二次调节处理，输出第一控制输入量；鲁棒补偿处理模块，用于对误差状态量进行鲁棒补偿处理，输出第二控制输入量；控制模块，用于采用反馈线性化方式，根据第一控制输入量和第二控制输入量，生成最终控制输入量，通过最终控制输入量对高速无人飞行器进行控制。

第三方面，本发明实施例提供了一种高速无人飞行器，上述高速无人飞行器的控制装置设置于高速无人飞行器中。

本发明实施例带来了以下有益效果：

本发明实施例提供的一种高速无人飞行器的控制方法、装置和高速无人飞行器，获取到高速无人飞行器输出的状态量后，根据期望状态和状态量计算误差状态量，对该误差状态量进行线性二次调节处理，输出第一控制输入量，再对该误差状态量进行鲁棒补偿处理，输出第二控制输入量；进而采用反馈线性化方式，根据第一控制输入量和第二控制输入量，生成最终控制输入量，通过最终控制输入量对高速无人飞行器进行控制；该方式利用高速无人飞行器动态系统的非线性信息，可以抑制多种不确定性对飞行器控制的影响，减少了传统飞行器控制方法的保守性，从而提高了控制精确度。

本发明的其他特征和优点将在随后的说明书中阐述，或者，部分特征和优点可以从说明书推知或毫无疑义地确定，或者通过实施本发明的上述技术即可得知。

为使本发明的上述目的、特征和优点能更明显易懂，下文特举较佳实施方式，并配合所附附图，作详细说明如下。

附图说明

为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施方式，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例提供的一种高速无人飞行器的控制方法的流程图；

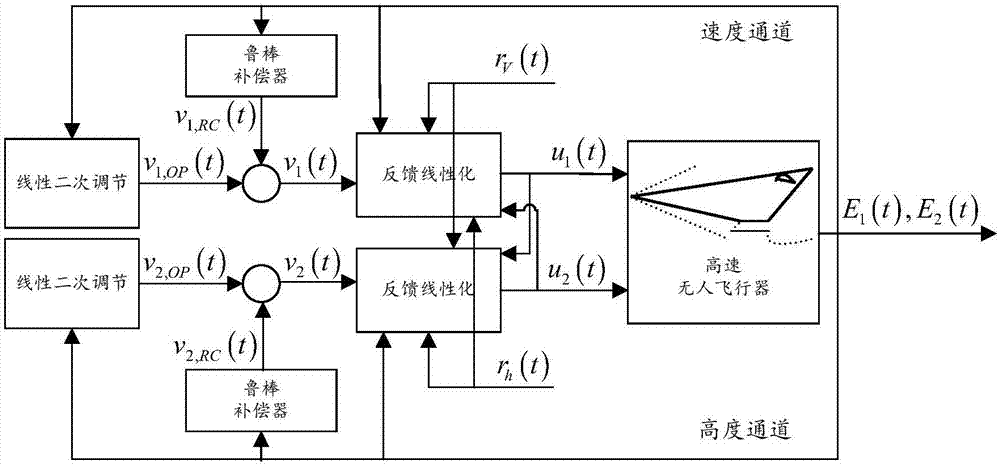
图2为本发明实施例提供的鲁棒非线性控制器的结构示意图；

图3为本发明实施例提供的忽略不确定性时，应用标称控制器和鲁棒非线性控制器的速度和高度响应效果图；

图4为本发明实施例提供的忽略不确定性时，应用标称控制器和鲁棒非线性控制器的航迹角、攻角和俯仰角速率响应效果图；

图5为本发明实施例提供的忽略不确定性时，应用标称控制器和鲁棒非线性控制器的控制输入效果图；

图6为本发明实施例提供的不确定模型应用标称控制器的速度和高度响应效果图；

图7为本发明实施例提供的不确定模型应用鲁棒非线性控制器的速度和高度响应效果图；

图8为本发明实施例提供的不确定模型应用标称控制器和鲁棒非线性控制器的航迹角、攻角和俯仰角速率响应效果图；

图9为本发明实施例提供的不确定模型应用标称线性控制器和鲁棒线性控制器的控制输入效果图；

图10为本发明实施例提供的不确定模型应用标称线性控制器的速度和高度响应效果图；

图11为本发明实施例提供的不确定模型应用鲁棒线性控制器的速度和高度响应效果图；

图12为本发明实施例提供的不确定模型应用标称线性控制器和鲁棒线性控制器的控制输入效果图；

图13为本发明实施例提供的一种高速无人飞行器的控制装置的结构示意图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合附图对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

考虑到现有的高速无人飞行器的控制方式难以抑制多种不确定性因素的影响，导致控制误差较大的问题，本发明实施例提供了一种高速无人飞行器的控制方法、装置和高速无人飞行器；该技术可以应用于高速无人飞行器的控制过程中；该技术可以采用相关的软件或硬件实现，下面通过实施例进行描述。

参见图1所示的一种高速无人飞行器的控制方法的流程图；该方法包括如下步骤：

步骤s102，获取高速无人飞行器输出的状态量；该状态量包括速度状态量和高度状态量；

步骤s104，根据期望状态和所述状态量计算误差状态量；该误差状态量包括速度误差状态量和高度误差状态量；

通常，高速无人飞行器的动力系统所对应的模型为非线性模型，为了实现对无人机飞行器的鲁棒控制，需要对高速无人飞行器的非线性模型进行线性化处理，获得线性模型，通过对线性模型设计标称控制器，可以实现期望的跟踪效果。

上述对高速无人飞行器的非线性模型进行线性化处理，获得线性模型的步骤，具体可以通过下述方式实现：

(1)高速无人飞行器的非线性模型为

其中，状态向量x1(t)＝[v(t)β(t)β(t)]^t，x2(t)＝[h(t)γ(t)α(t)q(t)]^t，v(t)为速度，γ(t)为航迹角，h(t)为高度，α(t)为攻角，q(t)为俯仰率；β(t)为节流阀开度；

输出向量y(t)＝[yi(t)]2×1＝[v(t)h(t)]^t，输入量u(t)＝[ui(t)]2×1＝[βc(t)δe(t)]^t，系统矩阵a(x(t))＝[ai(x(t))]7×1，输入矩阵b(x(t))＝[b1(x(t))b2(x(t))]7×2，输出矩阵c(x(t))＝[c1(x(t))c2(x(t))]^t分别表示状态的矢量场或矩阵场；

(2)引入输出矩阵c(x(t))＝[c1(x(t))c2(x(t))]^t的李导数

(3)对输出向量y(t)＝[yi(t)]2×1＝[v(t)h(t)]^t进行γi(i＝1,2)次为微分处理，得到线性模型

y^[γ](t)＝afl(x(t))+bfl(x(t))u(t)

其中，γ＝(γ1,γ2)表示向量的相对阶数，afl(x(t))为线性模型的系统矩阵，线性模型的输出矩阵bfl(x(t))是非奇异的。

步骤s106，对误差状态量进行线性二次调节处理，输出第一控制输入量；

该步骤s106具体可以通过下述方式实现：

(1)计算速度误差状态量e1(t)＝[e1,i(t)]4×1和高度误差状态量e2(t)＝[e2,i(t)]5×1；其中，e1,1(t)＝y1(t)-rv(t)，e2,1(t)＝y2(t)-rh(t)，和rv(t)和rh(t)分别为期望的速度参考信号和期望的高度参考信号；

(2)计算第一控制输入量vi,op(t)＝kop,iei(t),i＝1,2；其中，为最优控制增益；正实对称矩阵ri(i＝1,2)表示能量消耗的权重；pi(i＝1,2)为下式riccati方程的正定解：

步骤s108，对误差状态量进行鲁棒补偿处理，输出第二控制输入量；

该步骤s108具体可以通过下述方式实现：

计算第二控制输入量

其中，f1和f2为待确定的正参数；gi(s)(i＝1,2)为传递函数；s表示拉普拉斯算子；，yi(s)为输出量。

yi(s)＝cf,i(sii-aop,i)^-1(ei(0)+δi(s))+gi(s)vi,rc(s)i＝1,2.

ii为单位矩阵；aop,i＝af,i+bf,ikop,i(i＝1,2)，

δi(s)＝(sii-aop,i)ei(s)-bf,ivi,rc(s),i＝1,2。

步骤s110，采用反馈线性化方式，根据第一控制输入量和第二控制输入量，生成最终控制输入量，通过最终控制输入量对高速无人飞行器进行控制。

该步骤s110具体可以通过下述方式实现：

(1)根据第一控制输入量vi,op(t)和第二控制输入量数vi,rc(t)计算总控制输入量

vi(t)＝vi,op(t)+vi,rc(t),i＝1,2

(2)将总控制输入量vi(t)输入至反馈线性化控制器

其中，v(t)＝[v1(t)v2(t)]^t为第一控制输入量和第二控制输入量之和；

(3)将最终控制输入u(t)输入至高速无人飞行器的动力系统，以控制飞行状态。

本发明实施例提供的一种高速无人飞行器的控制方法，获取到高速无人飞行器输出的状态量后，根据期望状态和状态量计算误差状态量，对该误差状态量进行线性二次调节处理，输出第一控制输入量，再对该误差状态量进行鲁棒补偿处理，输出第二控制输入量；进而采用反馈线性化方式，根据第一控制输入量和第二控制输入量，生成最终控制输入量，通过最终控制输入量对高速无人飞行器进行控制；该方式利用高速无人飞行器动态系统的非线性信息，可以抑制多种不确定性对飞行器控制的影响，减少了传统飞行器控制方法的保守性，从而提高了控制精确度。

本发明实施例还提供了另一种高速无人飞行器的控制方法，该方法针对高速无人飞行器的纵向动力学控制问题，首先提出了一种由反馈线性化控制器和鲁棒线性控制器组成的鲁棒非线性控制器，并提供了一种高速无人飞行器的鲁棒非线性纵向控制器设计方式。具体地，该方法采用反馈线性化控制器实现纵向速度和高度通道的动态解耦；然后，基于所建立的线性模型设计鲁棒线性控制器，以抑制参数不确定性、外部干扰和部分非线性动力学的影响。该方法由于采用了动态系统的非线性信息，可以减少鲁棒控制器设计的保守性。

该方法通过下述步骤实现：

步骤一：选择高速无人飞行器纵向动力学模型。

本实施例选取吸气式高速无人飞行器纵向动力学模型，该模型可以用包括速度v(t)，航迹角γ(t)，高度h(t)，攻角α(t)，俯仰率q(t)的一组微分方程来描述，具体形式如下：

其中，m，μ和iyy分别表示高速无人飞行器质量、重力常数和转动惯量。di(t)(i＝v,γ,h,α,q)代表外部有界大气扰动，l(t)，d(t)，t(t)和mq(t)分别表示满足公式(2)的升力、阻力、推力和俯仰力矩。

其中，ρ，s和分别代表空气密度、参考面积和平均气动弦长，cl(t)，cd(t)，ct(t)和cmα(t)，cmδe(t)，cmq(t)分别表示推力系数和力矩系数。r＝h+re，re为地球半径，ρ0和h0是正常数。推力和力矩系数取决于攻角α和舵偏角δe。由于上述升力、阻力、推力和俯仰力之间的关系是不可解析的，因此用曲线拟合的方法推导出如下的气动系数表达式：

其中，β(t)表示节流阀开度，δci(t)(i＝1,2,…,7)表示未建模不确定性，代表曲线拟合的气动系数与真实值之间的不匹配度。未建模的不确定性被假定为范数有界，而不是简单地假设有界，这取决于攻角需满足下式：

其中，μα2i，μα1i和μα0i为正常数。超燃冲压发动机的动力学模型可以用下面的二阶系统描述：

其中，βc(t)表示表示节流阀开度指令，ξn和ωn为正常数，分别表示阻尼比和自然角频率，δc8(t)表示面向控制的发动机模型和真实模型之间的模型不匹配度。δc8(t)被认为是范数有界的，由正常数μδ2β，μδ1β和μδ0β表示如下：

从式(1)-式(4)可知高速无人飞行器动力学存在强耦合和高度非线性。推力和力矩系数包括攻角的平方项，这对鲁棒闭环控制系统设计提出了挑战。如果外部干扰di(t)(i＝v,γ,h,α,q)和未建模动态δci(t)(i＝1,2,…,8)被忽略，那么由式(1)-式(4)描述的模型为标称非线性模型。

控制目标是为式(1)-式(4)所表示的飞行器系统设计一个鲁棒的非线性控制器，使速度、节流阀开度及其导数、航迹角、高度、攻角和俯仰率有界，并且输出v(t)和h(t)可以分别跟踪参考信号rv(t)和rh(t)。假定参考速度和高度及其导数是有界的。

步骤二：设计鲁棒非线性控制器。

在本步骤中，将分三部分设计鲁棒非线性控制器来实现对高速无人飞行器的鲁棒控制。首先利用反馈线性化技术获得高速无人飞行器线性模型，并实现速度和高度通道的动态解耦。然后，针对所得到的线性解耦模型，分别设计线性二次型调节器和鲁棒补偿器两个鲁棒线性控制器。采用线性二次型调节方法，通过忽略不确定性，可以实现标称线性系统的期望跟踪性能。实际上，反馈线性化控制器和线性二次型调节器共同构成了标称控制器，而引入鲁棒补偿器则来用来抑制参数不确定性、外部干扰和部分非线性的影响。

(1)反馈线性化控制器设计

将复杂非线性系统转化为简单的等效线性系统有两种方法。一种方法是将非线性函数在平衡点附近进行泰勒级数展开，只保留线性项。这种方法在控制器设计中通常忽略了泰勒级数的高阶项，如果被忽略的项不够小，则将导致线性系统不精确。另一种方法是利用反馈线性化技术来获得设计控制器所需的线性模型。在本步骤中将采用反馈线性化方法来实现标称非线性系统输入输出的精确线性化。

由式(1)-式(4)描述的高速无人飞行器模型的标称部分可以重写为一般形式：

其中状态量x1(t)＝[v(t)β(t)β(t)]^t，x2(t)＝[h(t)γ(t)α(t)q(t)]^t，输出y(t)＝[yi(t)]2×1＝[v(t)h(t)]^t，输入u(t)＝[ui(t)]2×1＝[βc(t)δe(t)]^t，矩阵a(x(t))＝[ai(x(t))]7×1，b(x(t))＝[b1(x(t))b2(x(t))]7×2，c(x(t))＝[c1(x(t))c2(x(t))]^t表示状态的矢量或矩阵场。可见，系统控制输入u1(t)、u2(t)和输出y1(t)、y2(t)的矢量相对阶数分别是γ1＝3和γ2＝4，这意味着可以使用全状态反馈线性化。在这种情况下，有关矢量场a(x(t))和bi(x(t))(i＝1,2)的函数ci(x(t))(i＝1^,2)的李导数被引入如下：

因此，在对输出y1(t)和y2(t)微分γi(i＝1,2)次后，输出动态可以表示如下：

或者

y^[γ](t)＝afl(x(t))+bfl(x(t))u(t),(6)

其中γ＝(γ1,γ2)表示向量的相对阶数，如果bfl(x(t))是非奇异的，可以得到反馈控制律如下：

其中v(t)＝[v1(t)v2(t)]^t表示具有如下线性解耦输出动态形式的虚拟控制输入

y^[γ](t)＝v(t).(8)

虚拟控制输入vi(t)(i＝1,2)由两部分组成：最优控制输入vi,op(t)(i＝1,2)和鲁棒补偿输入vi,rc(t)(i＝1,2)：

vi(t)＝vi,op(t)+vi,rc(t),i＝1,2.(9)

(2)最优控制器设计

定义速度和高度通道的跟踪误差分别为e1(t)＝[e1,i(t)]4×1和e2(t)＝[e2,i(t)]5×1。其中，e1,1(t)＝y1(t)-rv(t)，e2,1(t)＝y2(t)-rh(t)，和那么，式(8)的线性化模型可以表示如下：

其中

δ1和δ2为等效干扰，包括参数不确定性、外部干扰和部分非线性等，这些干扰不能被反馈线性化技术完全抵消。

忽略不确定性因素δ1和δ2，下式为设计速度和高度通道最优控制器的代价函数：

其中，正实对称矩阵qi(i＝1,2)和ri(i＝1,2)分别表示跟踪误差和能量消耗的权重。线性二次型调节反馈控制器如下：

其中，pi(i＝1,2)为下式riccati方程的正定解：

定义最优控制增益那么，最优控制器可以重写为：

vi,op(t)＝kop,iei(t),i＝1,2.(11)

(3)设计鲁棒补偿器

引入鲁棒补偿器来抑制等效扰动δi(i＝1,2)对闭环控制系统的影响。定义aop,i＝af,i+bf,ikop,i(i＝1,2)，那么

设ii为单位矩阵，gi(s)(i＝1,2)为传递函数，如下式所示：

gi(s)＝cf,i(sii-aop,i)^-1bf,i,i＝1,2,(13)

其中，s表示拉普拉斯算子，由式(12)可以得到输入和输出之间的关系如下：

yi(s)＝cf,i(sii-aop,i)^-1(ei(0)+δi(s))+gi(s)vi,rc(s),i＝1,2.(14)

设计鲁棒补偿器，以减少等效扰动的影响，以如下形式给出：

其中f1(s)＝f1³/(s+f1)³和为鲁棒滤波器，f1和f2为待确定的正参数。如果滤波器参数具有较大的值，这样滤波器的增益将接近1。在这种情况下，可以抑制δi(t)(i＝1,2)对闭环控制系统的影响。由于δi(t)(i＝1,2)不能直接测量，可以通过以下方式重构鲁棒补偿输入。通过忽略初始状态，可以从式(12)中得到

δi(s)＝(sii-aop,i)ei(s)-bf,ivi,rc(s),i＝1,2.(16)

结合式(15)和式(16)，可以得到

参见图2所示的鲁棒非线性控制器的结构示意图；从图2中可以看出，反馈线性化后所设计的鲁棒线性控制器由一个最优控制器和一个鲁棒补偿器组成，是分布式的和时不变的。标称最优控制器回路能实现标称系统的闭环跟踪性能，而鲁棒补偿器将产生一个鲁棒信号来抑制等效扰动δi(t)(i＝1,2)对闭环控制系统的影响。

步骤三对鲁棒非线性控制器进行鲁棒性分析。

将式(15)代入到式(12)，可以得到

其中cj表示第j行为1其余为0的向量。由此可见，状态ei(t)(i＝1,2)可以被有限的范数界限制如下：

||ei||∞≤μei(0)+δi||δi||∞,i＝1,2,(19)

其中，(i＝1，2)是有界的正数并满足δi＝||(si-aop,i)^-1(1-fi)||∞(i＝1,2)和令和假定等效扰动的范数是有界的，如下所示：

其中φδe5i，φδe4i，φδe3i，φδe2i，φδe1i，φδci(i＝1,2)是正常数。

定理1：对于给定的有界初始误差e(0)和一个给定的正常数ε，存在正常数fm和tm使得如果fi≥ft(i＝1,2)，那么误差e(t)是有界的，并且

证明：存在正常数fπδ和πδ使得如果fi>fπδ(i＝1,2)，那么可以得到

δ≤πδ/fmin,(21)

其中δ＝maxiδi，fmin＝minifi。定义φδej＝maxiφδeji(j＝1,2,3,4,5)，φδc＝maxiφδci。由式(19)，式(20)和式(21)可知，如果鲁棒补偿器参数fi(i＝1,2)满足fmin≥πδ，那么δ≤πδ/fmin≤1，可以得到

此外，如果fmin满足

可以得到

其中，在这种情况下，下面的不等式成立：

将式(19)代入到式(20)中，可以得到

||δ||∞≤(μe(0)+δ||δ||∞)φδe(e)+φδc.(25)

由式(24)和式(25)可以推导出如下不等式

那么，由式(19)，式(21)和式(26)，可以得到

其中πef是正常数并满足

实际上，由式(22)可知，跟踪误差e(t)的吸引域如下：

{e(t):||e||∞≤χemax},(28)

其中χemax是关于e(t)等式的最大正实根：

因此，存在一个正数fχe，使得如果fmin≥fχe，可以得到

令，在这种情况下，对于任意的fmin≥fπe，如果e(t)起始于吸引域，那么它将一直留在这个域中。因此，不等式(22)成立。

由式(18)，式(21)和式(27)可以得到：

令fm＝max{fπδ,πδ,fχe,fπe,fεe}。那么，对于一个给定有界初始误差e(0)和一个给定正常数ε，存在一个正常数tm，使得如果fi≥fm(i＝1,2)，那么误差e(t)是有界的，并且

需要指出的是，如果fi(i＝1,2)选取较大的正值可以提高跟踪性能。在实际应用中，fi(i＝1,2)可以通过在线调节方法来确定：将鲁棒补偿器参数fi(i＝1,2)设置为较大的值，直到闭环控制系统达到预期的跟踪性能。

步骤四：对高速无人飞行器的闭环控制系统进行仿真验证

对步骤一和二中构建的闭环控制系统进行仿真，以检验鲁棒非线性控制器的跟踪特性。高速无人飞行器标称参数如下：m＝9375slugs，μ＝1.36×10¹⁶ft³/s²，iy＝7×10⁶slugs·ft²，r＝2.09035×10⁷ft，ρ0＝2.38×10^-3slugs/ft³，h0＝1.1×10⁵ft，s＝3603ft²，ωn＝20，ξn＝0.3。速度和高度通道的参考信号分别由下式给出：其中，vric(s)和hric(s)表示参考输入命令，λv＝0.4，λh＝0.4。

飞行器的速度需要从巡航速度15060ft/s加速到15260ft/s，然后降低到15060ft/s，同时飞行器高度需要从巡航高度110000ft爬升到111000ft，然后再降回巡航高度。仿真时间一共持续100s，控制器的参数选择如下：q1＝diag(0.34,0.86,47.93,8.54×10^-12),q2＝diag(2.35×10^-3,0.52,220.6,57.12,1.1×10^-12),r1＝0.12,r2＝1.05,f1＝50,andf2＝60。

下面将分三个步骤来验证设计的鲁棒非线性控制器的有效性：

步骤1：标称模型的仿真

忽略不确定性δi(t)(i＝1,2)，对标称模型进行仿真。将鲁棒非线性控制器的响应与标称控制器进行比较。参见图3所示的忽略不确定性时，应用标称控制器和鲁棒非线性控制器的速度和高度响应效果图；参见图4所示的忽略不确定性时，应用标称控制器和鲁棒非线性控制器的航迹角、攻角和俯仰角速率响应效果图；参见图5所示的忽略不确定性时，应用标称控制器和鲁棒非线性控制器的控制输入效果图。

速度和高度、航迹角、攻角、俯仰速率的响应和控制输入分别如图3、图4和图5所示。从图3-图5中可以看出，鲁棒非线性控制器和标称控制器都能获得良好的跟踪性能。反馈线性化技术可以抑制非线性和耦合对闭环控制系统的影响。鲁棒非线性控制器的控制输入幅值与标称控制器相似。

步骤2：不确定模型的仿真

考虑参数不确定性和外部干扰。所有飞行器参数和空气动力系数的值被假定为标称值的150％。外部干扰设置为：dv＝60,dh＝7×10^-3,dγ＝-8×10^-2,dα＝2×10^-2,dq＝-10^-2,δc8＝-6。参见图6所示的不确定模型应用标称控制器的速度和高度响应效果图；参见图7所示的不确定模型应用鲁棒非线性控制器的速度和高度响应效果图；参见图8所示的不确定模型应用标称控制器和鲁棒非线性控制器的航迹角、攻角和俯仰角速率响应效果图；参见图9所示的不确定模型应用标称线性控制器和鲁棒线性控制器的控制输入效果图；

速度和高度、航迹角、攻角、俯仰速率的响应和控制输入如图6-图9所示。从图6-图9中可以看出，鲁棒非线性控制器在多个不确定因素的影响下仍能保持良好的跟踪性能，而标称控制器在闭环控制系统中存在明显的跟踪误差。速度和高度通道的鲁棒控制输入分别比标称控制输入稍大，而不确定性对闭环控制系统的影响可以通过鲁棒控制方法加以抑制。

步骤3：比较鲁棒非线性控制器与鲁棒线性控制器的跟踪性能

将鲁棒非线性控制器的跟踪性能与鲁棒线性控制器的跟踪性能进行比较。通过对平衡点的泰勒级数展开，得到了飞行器线性模型。然后，通过选择相同的控制器参数qi,ri,和fi(i＝1,2)，建立线性模型的标称线性控制器和鲁棒线性控制器。参见图10所示的不确定模型应用标称线性控制器的速度和高度响应效果图；参见图11所示的不确定模型应用鲁棒线性控制器的速度和高度响应效果图；参见图12所示的不确定模型应用标称线性控制器和鲁棒线性控制器的控制输入效果图。

速度和高度响应和控制输入如图10-图12所示。因为鲁棒控制输入可能接近无穷大，仿真在50秒时停。从图10可以看出，标称线性控制器的跟踪误差比在步骤2中的标称非线性控制器的跟踪误差大。从图11中可以看出，跟踪误差不能收敛，闭环控制系统不稳定。从图12中可以看出，鲁棒线性控制输入非常大。与此相反，采用鲁棒非线性控制方法，控制输入的幅值要小得多，速度和高度通道的跟踪误差可以收敛到原点的给定邻域。由于在控制器设计中充分利用了动态系统的非线性信息，减少了鲁棒控制器的设计保守性，降低了控制输入的幅值。

上述方法中鲁棒非线性控制器是分布式的和线性时不变的，并采用了动态系统的非线性信息，可以减少传统鲁棒线性控制器设计的保守性，降低了控制输入的幅值；该鲁棒非线性控制器还可以保证速度和高度的跟踪误差在有限的时间内收敛到给定邻域内。

对应于上述方法实施例，参见图13所示的一种高速无人飞行器的控制装置的结构示意图；该装置包括：

状态量获取模块130，用于获取高速无人飞行器输出的状态量；该状态量包括速度状态量和高度状态量；

误差状态量计算模块131，用于根据期望状态和所述状态量计算误差状态量；误差状态量包括速度误差状态量和高度误差状态量；

二次调节处理模块132，用于对误差状态量进行线性二次调节处理，输出第一控制输入量；

鲁棒补偿处理模块133，用于对误差状态量进行鲁棒补偿处理，输出第二控制输入量；

控制模块134，用于采用反馈线性化方式，根据第一控制输入量和第二控制输入量，生成最终控制输入量，通过最终控制输入量对高速无人飞行器进行控制。

上述装置还包括：线性化处理模块，用于对高速无人飞行器的非线性模型进行线性化处理，获得线性模型。

上述线性化处理模块，还用于：

高速无人飞行器的非线性模型为

其中，状态向量x1(t)＝[v(t)β(t)β(t)]^t，x2(t)＝[h(t)γ(t)α(t)q(t)]^t，v(t)为速度，γ(t)为航迹角，h(t)为高度，α(t)为攻角，q(t)为俯仰率；β(t)为节流阀开度；

输出向量y(t)＝[yi(t)]2×1＝[v(t)h(t)]^t，输入量u(t)＝[ui(t)]2×1＝[βc(t)δe(t)]^t，系统矩阵a(x(t))＝[ai(x(t))]7×1，输入矩阵b(x(t))＝[b1(x(t))b2(x(t))]7×2，输出矩阵c(x(t))＝[c1(x(t))c2(x(t))]^t；

引入输出矩阵c(x(t))＝[c1(x(t))c2(x(t))]^t的李导数

对输出向量y(t)＝[yi(t)]2×1＝[v(t)h(t)]^t进行γi(i＝1,2)次微分处理，得到线性模型

y^[γ](t)＝afl(x(t))+bfl(x(t))u(t)

其中，γ＝(γ1,γ2)表示向量的相对阶数，afl(x(t))为线性模型的系统矩阵，线性模型的输出矩阵bfl(x(t))是非奇异的。。

本发明实施例提供的一种高速无人飞行器的控制装置，获取到高速无人飞行器输出的状态量后，根据期望状态和状态量计算误差状态量，对该误差状态量进行线性二次调节处理，输出第一控制输入量，再对该误差状态量进行鲁棒补偿处理，输出第二控制输入量；进而采用反馈线性化方式，根据第一控制输入量和第二控制输入量，生成最终控制输入量，通过最终控制输入量对高速无人飞行器进行控制；该方式通过利用高速无人飞行器动态系统的非线性信息，可以抑制多种不确定性对飞行器控制的影响，减少了传统飞行器控制方法的保守性，从而提高了控制精确度。

本发明实施例还提供了一种高速无人飞行器，上述高速无人飞行器的控制装置设置于该高速无人飞行器中。

本发明实施例提供的高速无人飞行器，与上述实施例提供的高速无人飞行器的控制方法和装置具有相同的技术特征，所以也能解决相同的技术问题，达到相同的技术效果。

本发明实施例所提供的高速无人飞行器的控制方法、装置和高速无人飞行器的计算机程序产品，包括存储了程序代码的计算机可读存储介质，所述程序代码包括的指令可用于执行前面方法实施例中所述的方法，具体实现可参见方法实施例，在此不再赘述。

所述功能如果以软件功能单元的形式实现并作为独立的产品销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件产品的形式体现出来，该计算机软件产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：u盘、移动硬盘、只读存储器(rom，read-onlymemory)、随机存取存储器(ram，randomaccessmemory)、磁碟或者光盘等各种可以存储程序代码的介质。

最后应说明的是：以上所述实施例，仅为本发明的具体实施方式，用以说明本发明的技术方案，而非对其限制，本发明的保护范围并不局限于此，尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，其依然可以对前述实施例所记载的技术方案进行修改或可轻易想到变化，或者对其中部分技术特征进行等同替换；而这些修改、变化或者替换，并不使相应技术方案的本质脱离本发明实施例技术方案的精神和范围，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应所述以权利要求的保护范围为准。