一种基于STM32F407ZET6的木球挥杆速度检测系统的制作方法

本发明涉及单片机嵌入式实时数据采集及处理、数据可视化等技术，尤其是一种基于stm32f407zet6的木球挥杆速度检测系统。

背景技术：

木球运动是一项新兴的运动项目，由于其独特的运动魅力和锻炼价值，迅速普及开来，深受各国人民的欢迎。木球运动已从亚洲发展到了全世界，至今已举办多次国际竞赛。

然而，许多的木球运动员和爱好者受限于时间、地点等种种因素，难以广泛的获得具有针对性的指导，运动水平的进步被拖累。而如果有一个便携的设备能够实时读取木球运动者在挥杆击打木球时的实时速度，则可以较为方便快捷的反映运动者对于木球杆的控制水平，进而通过对比历史运动数据和他人运动数据，得到具有针对性的木球挥杆技术优化的建议。

技术实现要素：

为了克服已有及时无法实时检测木球挥杆速度的不足,本发明提供了一种有效检测木球挥杆速度的基于stm32f407zet6的木球挥杆速度检测系统。

本发明解决其技术问题所采用的技术方案是：

一种基于stm32f407zet6的木球挥杆速度检测系统，所述系统包括tft触摸屏控制模块、mpu-6050陀螺仪采集角速度模块和数据处理模块；

所述tft触摸屏控制模块中，屏幕触点坐标计算过程如下：

计算y坐标，在y+电极施加驱动电压vdrive，y-电极接地，x+作为引出端测量得到接触点的电压，由于ito层均匀导电，触点电压与vdrive电压之比等于触点y坐标与屏高度之比；

计算x坐标，在x+电极施加驱动电压vdrive，x-电极接地，y+做为引出端测量得到接触点的电压，由于ito层均匀导电，触点电压与vdrive电压之比等于触点x坐标与屏宽度之比；

测得的电压由adc转化为数字信号，再进行处理作为坐标判断触点的实际位置；

所述mpu-6050陀螺仪采集角速度模块中，定义坐标系如下：令芯片表面朝向自己，将其表面文字转至正确角度，此时，以芯片内部中心为原点，水平向右的为x轴，竖直向上的为y轴，指向自己的为z轴，三轴角速度对应的地址如下：

0x43为绕x轴旋转的角速度gyr_x

0x45为绕y轴旋转的角速度gyr_y

0x47为绕z轴旋转的角速度gyr_z

绕x、y和z三个座标轴旋转的角速度分量gyr_x、gyr_y和gyr_z均为16位有符号整数；从原点向旋转轴方向看去，取正值时为顺时针旋转，取负值时为逆时针旋转；

三个角速度分量均以“度/秒”为单位，能够表示的角速度范围，即倍率统一设定；

所述数据处理模块中，mpu-6050陀螺仪返回的数据经过转换得到实际测量的角速度数据。

进一步，所述数据处理模块中，对角速度值进行滤波，考虑到传感器噪声为高斯噪声，因此选用卡尔曼滤波对角速度数据进行处理。

再进一步，所述卡尔曼滤波过程中，先引入一个离散控制过程的系统，该系统用一个线性随机微分方程来描述：x(k)＝ax(k-1)+bu(k)+w(k)，再加上系统的测量值：z(k)＝hx(k)+v(k)；其中，x(k)是k时刻的系统状态，u(k)是k时刻对系统的控制量；a和b是系统参数，对于多模型系统，它们为矩阵；z(k)是k时刻的测量值，h是测量系统的参数，对于多测量系统，h为矩阵；w(k)和v(k)分别表示过程和测量的噪声，它们被假设成高斯白噪声，covariance分别是q，r；

用covariances来估算系统的最优化输出，首先利用系统的过程模型，来预测下一状态的系统；假设现在的系统状态是k，根据系统的模型，基于系统的上一状态而预测出现在状态：x(k|k-1)＝ax(k-1|k-1)+bu(k)…(1)

式(1)中，x(k|k-1)是利用上一状态预测的结果，x(k-1|k-1)是上一状态最优的结果，u(k)为现在状态的控制量，如果没有控制量，它可以为0；

用p表示covariance：p(k|k-1)＝ap(k-1|k-1)a’+q(2)

式(2)中，p(k|k-1)是x(k|k-1)对应的covariance，p(k-1|k-1)是x(k-1|k-1)对应的covariance，a’表示a的转置矩阵，q是系统过程的covariance；

得到了现在状态的预测结果，然后再收集现在状态的测量值；结合预测值和测量值，得到现在状态(k)的最优化估算值x(k|k)：x(k|k)＝x(k|k-1)+kg(k)(z(k)-hx(k|k-1))……(3)

其中kg为卡尔曼增益(kalmangain)：kg(k)＝p(k|k-1)h’/(hp(k|k-1)h’+r)………(4)

为了卡尔曼滤波器不断的运行下去直到系统过程结束，还要更新k状态下x(k|k)的covariance：p(k|k)＝(i-kg(k)h)p(k|k-1)………(5)

其中i为1的矩阵，对于单模型单测量，i＝1；当系统进入k+1状态时，p(k|k)就是式子(2)的p(k-1|k-1)；这样就可以自回归的运算下去。

所述tft触摸屏控制模块中，采用5点中值滤波，即当前时刻的x坐标将由前4个时刻的点的x坐标和当前时刻实际采集到的x坐标中值决定，当前时刻的y坐标将由前4个时刻的点的y坐标和当前时刻实际采集到的y坐标中值决定，操作如下：将前4个时刻与当前时刻的x、y的坐标值存入数组中，然后将x、y数组排序，取其下标为2的元素值并作为当前时刻值，不断重复该操作即可。

本发明中，本发明利用意法半导体公司的stm32f407zet6这款基于armcortex^tm-m4内核的处理器，结合tft触摸屏，mpu-6050陀螺仪等一系列外部设备，实现对进行木球运动时的挥杆速度的有效采集，经过stm32f407zet6内核对数据进行滤波与换算，得到最终结果，并利用显示屏显示数据，以达到数据可视化的目的。

本发明的有益效果主要表现在：获得更精确的角速度值，实现高精度控制。

附图说明

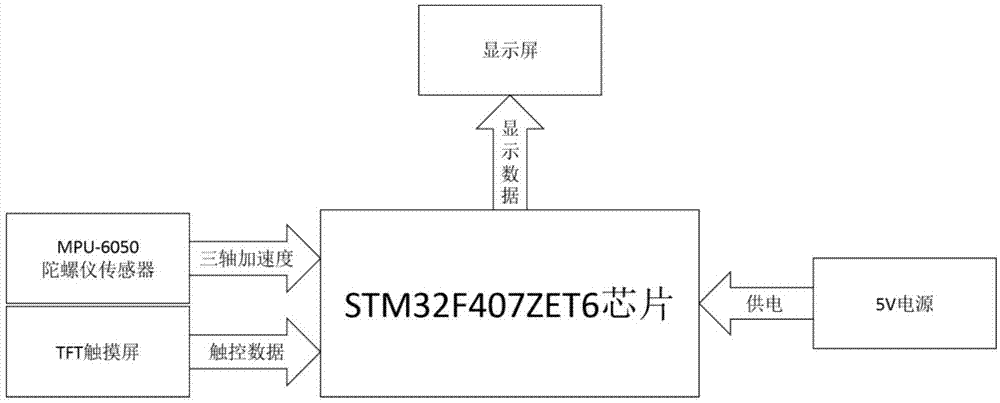
图1是基于stm32f407zet6的木球挥杆速度检测系统的原理图。

具体实施方式

下面结合附图对本发明作进一步描述。

参照图1，一种基于stm32f407zet6的木球挥杆速度检测系统，包括tft触摸屏控制模块、mpu-6050陀螺仪采集角速度模块和数据处理模块；

所述tft触摸屏控制模块中，屏幕触点坐标计算过程如下：

计算y坐标，在y+电极施加驱动电压vdrive，y-电极接地，x+作为引出端测量得到接触点的电压，由于ito层均匀导电，触点电压与vdrive电压之比等于触点y坐标与屏高度之比；

计算x坐标，在x+电极施加驱动电压vdrive，x-电极接地，y+做为引出端测量得到接触点的电压，由于ito层均匀导电，触点电压与vdrive电压之比等于触点x坐标与屏宽度之比；

测得的电压由adc转化为数字信号，再进行处理作为坐标判断触点的实际位置；

在实际情况中，tft屏幕触点坐标存在随机误差，因此需要减小误差影响，根据误差的特性，采用的算法是5点中值滤波，即当前时刻的x坐标将由前4个时刻的点的x坐标和当前时刻实际采集到的x坐标中值决定，当前时刻的y坐标将由前4个时刻的点的y坐标和当前时刻实际采集到的y坐标中值决定，操作如下：将前4个时刻与当前时刻的x、y的坐标值存入数组中，然后将x、y数组排序，取其下标为2的元素值并作为当前时刻值，不断重复该操作即可。

所述mpu-6050陀螺仪采集角速度模块中，mpu-6050系列为全球第一个整合性6轴运动处理组件。它集成了陀螺仪与三轴加速度计，与此同时很好的解决了两者的时间差问题。工作稳定且高效，同时节约了大量的封装空间。不仅于此，它还具有较强的可拓展性和通信能力。mpu6050内部自带了可扩展的数字运动处理器dmp使得其可以拓展地磁计等众多其他多轴传感器，而扩展之后的数据可以通过其内部的i2c接口或spi接口输出，有利于使用。

mpu6050芯片的坐标系是这样定义的：令芯片表面朝向自己，将其表面文字转至正确角度，此时，以芯片内部中心为原点，水平向右的为x轴，竖直向上的为y轴，指向自己的为z轴，根据技术手册，三轴角速度对应的地址如下：

0x43为绕x轴旋转的角速度gyr_x

0x45为绕y轴旋转的角速度gyr_y

0x47为绕z轴旋转的角速度gyr_z

绕x、y和z三个座标轴旋转的角速度分量gyr_x、gyr_y和gyr_z均为16位有符号整数；从原点向旋转轴方向看去，取正值时为顺时针旋转，取负值时为逆时针旋转。

三个角速度分量均以“度/秒”为单位，能够表示的角速度范围，即倍率可统一设定，有4个可选倍率：250度/秒、500度/秒、1000度/秒、2000度/秒。以gyr_x为例，若倍率设定为250度/秒，则意味着gyr取正最大值32768时，当前角速度为顺时针250度/秒；若设定为500度/秒，取32768时表示当前角速度为顺时针500度/秒。显然，倍率越低精度越好，倍率越高表示的范围越大。

用f表示倍率，f＝0为250度/秒，f＝3为2000度/秒。以gyr_x为例，若当前设定的角速度倍率为1000度/秒，那么将gyr_x读数换算为角速度(顺时针)的公式为：g_x＝1000×gyr_x/32768。利用该公式即可求出实际的角速度值。

所述数据处理模块中，mpu-6050陀螺仪返回的数据经过转换得到实际测量的角速度数据，但是由于传感器存在噪声，导致结果存在一定偏差，需要对角速度值进行滤波，考虑到传感器噪声多为高斯噪声，因此选用卡尔曼滤波对角速度数据进行处理。

卡尔曼滤波原理如下：先引入一个离散控制过程的系统，该系统可用一个线性随机微分方程(linearstochasticdifferenceequation)来描述：x(k)＝ax(k-1)+bu(k)+w(k)，再加上系统的测量值：z(k)＝hx(k)+v(k)；其中，x(k)是k时刻的系统状态，u(k)是k时刻对系统的控制量。a和b是系统参数，对于多模型系统，他们为矩阵。z(k)是k时刻的测量值，h是测量系统的参数，对于多测量系统，h为矩阵。w(k)和v(k)分别表示过程和测量的噪声，它们被假设成高斯白噪声(whitegaussiannoise)，covariance分别是q，r。

对于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。

用covariances来估算系统的最优化输出。首先利用系统的过程模型，来预测下一状态的系统。假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态：x(k|k-1)＝ax(k-1|k-1)+bu(k)…(1)

式(1)中，x(k|k-1)是利用上一状态预测的结果，x(k-1|k-1)是上一状态最优的结果，u(k)为现在状态的控制量，如果没有控制量，它可以为0；

用p表示covariance：p(k|k-1)＝ap(k-1|k-1)a’+q(2)

式(2)中，p(k|k-1)是x(k|k-1)对应的covariance，p(k-1|k-1)是x(k-1|k-1)对应的covariance，a’表示a的转置矩阵，q是系统过程的covariance。式子(1)，(2)就是卡尔曼滤波器5个公式当中的前两个，也就是对系统的预测。

得到了现在状态的预测结果，然后再收集现在状态的测量值。结合预测值和测量值，可以得到现在状态(k)的最优化估算值x(k|k)：x(k|k)＝x(k|k-1)+kg(k)(z(k)-hx(k|k-1))……(3)

其中kg为卡尔曼增益(kalmangain)：kg(k)＝p(k|k-1)h’/(hp(k|k-1)h’+r)………(4)

为了卡尔曼滤波器不断的运行下去直到系统过程结束，还要更新k状态下x(k|k)的covariance：p(k|k)＝(i-kg(k)h)p(k|k-1)………(5)

其中i为1的矩阵，对于单模型单测量，i＝1。当系统进入k+1状态时，p(k|k)就是式子(2)的p(k-1|k-1)。这样，算法就可以自回归的运算下去。

根据这5个公式，可以很容易的实现对mpu6050角速度的滤波，从而获得更精确的角速度值，实现高精度控制。

本实施例的工作过程包括以下步骤：

①将设备电路连接完成。

②将设备主体部分绑定在手臂上，mpu6050芯片绑定在手背上。

③打开设备电源，tft触控屏上显示“start”字样。

④点击tft触摸屏上的“start”，设备开始记录挥杆过程的速度。

⑤挥动手中的木球杆进行击球。

⑥击球结束，tft显示屏显示挥杆速度-时间图像，横轴代表从挥杆开始后所经过时间t，纵轴代表t时刻手掌绕肩部旋转的角速度ω。

⑦对比此次挥杆速度-时间曲线与标准挥杆的速度-时间曲线，改进挥杆动作。