基于集群控制的多无人机协同目标监视控制方法与流程

本公开涉及多无人机集群控制技术领域，尤其涉及一种基于集群控制的多无人机协同目标监视控制方法。

背景技术：

采用无人机对某一固定目标进行绕飞具有广泛的应用。在军用领域，即可用于对敌方军事目标的侦察监视，也可用于对我方人员的提供空中支援与保护；在民用领域，搭载图像采集设备的无人机已广泛应用于对电塔等目标的巡检。若采用多个无人机绕某一固定目标以不同的半径进行绕飞，这样形成内环与外环，军事上外环无人机可作为防御无人机，内环无人机用于实际工作，民用上外环也可作为内环无人机的备份与协助，提高系统可靠性与工作效率。

现有技术中的绕飞方案一般采用一架无人机对目标进行绕飞，或多架无人机编队控制。

然而在实现本公开的过程中，本申请发明人发现，采用一架无人机对目标进行绕飞，其工作效率与系统可靠性远远低于多架无人机绕飞，此外，该方案中大多是通过工作人员手动遥控，即使有少量的自动化巡视方案，其自主化程度也不高；多无人机编队控制虽然是多无人机协同自主飞行，但其编队形式大多是三角编队等，即使有圆周编队也无法实现对无人机相位(航向角)的协同控制，即无法实现让所有无人机做圆周运动的同时还能让它们的相位保持同步状态(所有无人机具有相同的航向角)或平衡状态(所有无人机的航向角均匀的分布在一个圆周上)。

公开内容

(一)要解决的技术问题

基于上述技术问题，本公开提供一种基于集群控制的多无人机协同目标监视控制方法，以缓解现有技术中的无人机控制方案大多通过工作人员手动操控，自主化程度地，无法实现让所有无人机做圆周运动的同时还能让它们的相位保持同步状态或平衡状态的技术问题。

(二)技术方案

本公开提供一种基于集群控制的多无人机协同目标监视控制方法，使n架无人机从其各自的初始位置，以任意初始速度出发，围绕同一个圆心以不同的半径做圆周运动，且达到稳定状态时，n架所述无人机进入同步监视模式或平衡监视模式，n≥2，包括：

步骤a：建立目标方程，使所述目标方程求出极小值时n架所述无人机的相位达到期望的相位分布；

步骤b：求取该目标方程取得极小值过程中的下降方向；

步骤c：基于该下降方向，设计n架所述无人机的控制率；

步骤d：迭代计算所述控制率，将所述目标方程对应的控制率发送至n架所述无人机；

步骤e：重复步骤d，直至n架所述无人机终止监视模式。

在本公开的一些实施例中，所述步骤a中，所述目标方程由以下多个方程定义：

其中，zm＝xm+iym，m＝1，...，n，c＝[c1，...，cn]^t，cm表示n架所述无人机中第m架无人机以固定的巡航速度vm和角频率ωc进行圆周运动时，该圆形轨迹的圆心，θ＝[θ1，...，θn]^t，θ的每一个元素对应每个无人机的相位角；当fc(θ)取得极小值时，n架所述无人机围绕一个共同的圆心做圆周运动，当fpθ(θ)到达其惟一的极大值点时，n架所述无人机进入同步监视模式，当fpθ(θ)到达其惟一的极小值点时，n架所述无人机进入平衡监视模式。

在本公开的一些实施例中，所述步骤a中：

同步监视模式下的目标方程如下所示：

其中：当fa(θ)取得极小值时，fc(θ)取得极小值，且到达其惟一的极大值点；

平衡监视模式下的目标方程如下所示：

其中：当fb(θ)取得极小值时，fc(θ)取得极小值，且到达其惟一的极小值点；

其中，

在本公升的一些实施例中，所述步骤b中，根据levenberg-marquardt算法，求取该目标方程取得极小值过程中的下降方向。

在本公开的一些实施例中，所属步骤b中：

同步监视模式下的目标方程的下降方向如下式所示：

其中，ja为fa(θ)的一阶偏导数，

平衡监视模式下的目标方程的下降方向如下式所示：

其中，jb为fb(θ)的一阶偏导数，

在本公开的一些实施例中，所述步骤c中：

同步监视模式下的控制率如下式所示：

θk+1＝θk+da，k+ωc

平衡监视模式下的控制率如下式所示：

θk+1＝θk+db，k+ωc

其中，ωc为n个无人机最终期望的做圆周运动的角速度，k+1、k表示n架所述无人机的第k+1和k次采样时刻。

在本公开的一些实施例中，所述步骤d包括：步骤d1：参数初始化，包括：设定每架所述无人机的巡航速度vm与角频率ωc，m＝1，2，...，n，令k＝0；步骤d2：令k＝k+1；步骤d3：将所述步骤c设计的控制率进行迭代运算；步骤d4：若所述目标方程的函数值没有减小，更新阻尼系数，并返回步骤d3重新进行迭代运算，否则进入步骤d5；步骤d5：若目标方程的函数值取得极小值，将此时得出的控制率反馈至n架所述无人机，并返回步骤d2，否则继续执行迭代运算。

在本公开的一些实施例中，其中：所述步骤d1中，参数初始化还包括：令β∈(0，1)；所述步骤d4中，令fnew＝f(θk+1)，所述目标方程的函数值没有减小的判断依据为：fnew＞f(θk)+βg^t(θk)dk。

在本公开的一些实施例中，其中：所述步骤d1中，参数初始化还包括：令阻尼系数μ＞0，υ＞1：所述步骤d4中，更新阻尼系数的方式为：令μ＝μ*υ。

在本公开的一些实施例中，其中：所述步骤d1中，参数初始化还包括：设定精度参数eps，且令其逼近于0；所述步骤d5中，令tol＝||dk||；所述目标方程的函数值取得极小值的判断依据是：tol≤eps。

(三)有益效果

从上述技术方案可以看出，本公开提供的基于集群控制的多无人机协同目标监视控制方法具有以下有益效果的其中之一或其中一部分：

(1)本公开提供的基于集群控制的多无人机协同目标监视控制方法，能够使多架无人机进行协同作业，增强巡视效果(多架无人机协同巡视，可以弥补一架无人机巡视精度不够的缺点)并提升系统可靠性(即使某架无人机出现问题仍有其他无人机可以正常工作)；

(2)本公开提供的基于集群控制的多无人机协同目标监视控制方法相比于现有技术中的手动遥控方案自主化程度高；

(3)本公开提供的基于集群控制的多无人机协同目标监视控制方法能够使所有无人机做圆周运动的同时还能让它们的相位保持同步状态或平衡状态，而这两种相位分布相比于仅使用多架无人机绕飞而没有相关相位协同具有各自优势，比如，若多架无人机具有同步相位分布，内圈的无人机可以用来执行任务，外圈的无人机可以用来保护内圈的无人机，执行外围警戒；若多架无人机具有平衡相位分布，这种具有平衡相位分布的协同绕飞可以用来保护圆心位置上的目标，因多架无人机在多个同心圆上以均匀分布的相位飞行，大大增加了敌方无人机突防攻击的难度；

(4)本公开提供的基于集群控制的多无人机协同目标监视控制方法可用于电力巡检领域的对电塔进行绕飞检测，军用领域对敌方军事目标进行侦察监视等应用场景中。

附图说明

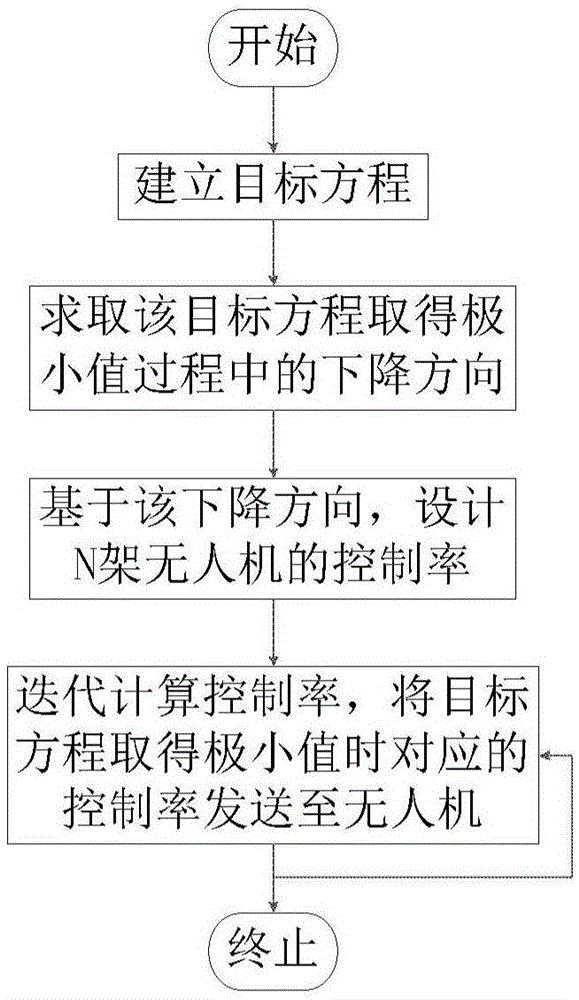
图1为本公开提供的基于集群控制的多无人机协同目标监视控制方法的步骤流程图。

图2为本公开提供的基于集群控制的多无人机协同目标监视控制方法的运算逻辑结构图。

图3为利用本公开提供的基于集群控制的多无人机协同目标监视控制方法控制3架无人机实现同步监视模式的仿真结果图。

图4为利用本公开提供的基于集群控制的多无人机协同目标监视控制方法控制2架无人机实现平衡监视模式的仿真结果图。

具体实施方式

本公开提供的基于集群控制的多无人机协同目标监视控制方法能够使多架无人机进行协同作业，增强巡视效果并提升系统可靠性。

为使本公开的目的、技术方案和优点更加清楚明白，以下结合具体实施例，并参照附图，对本公开进一步详细说明。

本公开提供一种基于集群控制的多无人机协同目标监视控制方法，使n架无人机从其各自的初始位置，以任意初始速度出发，围绕同一个圆心以不同的半径做圆周运动，且达到稳定状态时，n架无人机进入同步监视模式(所有无人机具有相同的航向角)或平衡监视模式(所有无人机的航向角均匀的分布在一个圆周上)，n≥2，如图1所示，包括：

步骤a：建立目标方程，使目标方程求出极小值时n架无人机的相位达到期望的相位分布；

步骤b：求取该目标方程取得极小值过程中的下降方向；

步骤c：基于该下降方向，设计n架无人机的控制率；

步骤d：迭代计算控制率，将目标方程对应的控制率发送至n架无人机；

步骤e：重复步骤d，直至n架无人机终止监视模式。

为使本公开实施例提供的基于集群控制的多无人机协同目标监视控制方法更便于理解，以下通过建立系统模型，对本公开实施例提供的基于集群控制的多无人机协同目标监视控制方法进行解释说明：

在一组含有n个无人机的无人机集群中，第m个无人机的系统模型描述为：

其中θ^m是第m个无人机的相位角，x^m，是第m个无人机的位置坐标，m＝1，...，n。δt是采样时间，假定无人机m有一个正的定常巡航速度vm＞0，且是其控制输入，为了便于分析，在本实施例中，省略δt，并且上标m和下标m具有相同的含义。

为了定义一组n个无人机需要形成的两种期望形式(同步监视模式和平衡监视模式)的相位分布，首先通过下式定义参数pθ：

同步相位分布的定义为：当所有无人机的相位都相同时，对于m，n＝1，...，n，随着t→∞，|pθ|→1，即：随着t→∞，θm-θn→0；

平衡相位分布的定义为：各个无人机的相位值使得随着t→∞，|pθ|→0。

假定第m架无人机以固定的巡航速度vm和角频率ωc进行圆周运动，则此圆周的半径rm＝vm/|ωc|，令zm＝xm+iym，可求得此圆周的圆心为

定义投影矩阵令c＝[c1，...，cn]^t，当且仅当

时，所有无人机运动轨迹的圆心将会重合，基于此，定义如下的目标方程

其中定义如下：

对于m＝1，...，n，当且仅当fc(θ)取得其惟一的极小值时，pc＝0；至此，实现了令一组无人机围绕一个共同的圆心做圆周运动，在此基础上，为了使多架无人机的相位达到期望的相位分布，定义如下的目标的方程

其中，θ＝[θ1，...，θn]^t，θ的每一个元素对应每个无人机的相位角；当达到其惟一的极大值点时，所有无人机的相位角相同；当达到其惟一极小值点时，所有无人机的相位平衡。

因此，在本公开的一些实施例中，步骤a中，目标方程由以下多个方程定义：

当fc(θ)取得极小值时，n架所述无人机围绕一个共同的圆心做圆周运动，当到达其惟一的极大值点时，n架所述无人机进入同步监视模式，当到达其惟一的极小值点时，n架所述无人机进入平衡监视模式。

在本公开的一些实施例中，为了实现上述两个目标：令所有无人机围绕同一圆心以不同半径做圆周运动并实现两种期望的相位分布模式，设计如下的目标方程在步骤a中：

同步监视模式下的目标方程如下所示：

其中：当fa(θ)取得极小值时，fc(θ)取得极小值，且到达其惟一的极大值点；

平衡监视模式下的目标方程如下所示：

其中：当fb(θ)取得极小值时，fc(θ)取得极小值，且到达其惟一的极小值点；

其中，umαx为的极大值，且

在本公开的一些实施例中，寻求目标函数fa(θ)或fb(θ)的极小值的过程实际是解决最小二乘问题，因此在步骤b中，采用解决此类问题比较有效的levenbeg-marquardt方法来求取该目标方程取得极小值过程中的下降方向。

在本公开的一些实施例，所述步骤b中，根据levenbeg-marquardt方法：

同步监视模式下的目标方程的下降方向如下式所示：

其中，ja为fa(θ)的一阶偏导数，

平衡监视模式下的目标方程的下降方向如下式所示：

其中，jb为fb(θ)的一阶偏导数，

在本公开的一些实施例中，为了能够让无人机做圆周运动，基于上述下降方向，步骤c中：

设计同步监视模式下的控制率如下式所示：

θk+1＝θk+da，k+ωc

设计平衡监视模式下的控制率如下式所示：

θk+1＝θk+db，k+ωc

其中，ωc为n个无人机最终期望的做圆周运动的角速度，k+1、k表示n架所述无人机的第k+1和k次采样时刻。

在本公开的一些实施例中，如图2所示，步骤d包括：

步骤d1：参数初始化，包括：设定每架所述无人机的巡航速度vm(即在协同控制开始时各个无人机的初始巡航速度)与角频率ωc(即最终期望的多个无人机做圆周运动的角速度)，m＝1，2，...，n，令k＝0，β∈(0，1)，阻尼系数μ＞0，系数υ＞1，设定精度参数eps，且令其逼近于0(例如：eps＝10^-6)；

步骤d2：令k＝k+1；

步骤d3：将所述步骤c设计的控制率进行迭代运算；

步骤d4：令fnew＝f(θk+1)，若fnew＞f(θk)+βg^t(θk)dk，说明目标方程的函数值没有减小，此时更新阻尼系数令μ＝μ*υ，并返回步骤d3重新进行迭代运算，否则进入步骤d5；

步骤d5：令tol＝||dk||，若tol≤eps，说明此时目标方程的函数值取得极小值，将此时得出的控制率反馈至n架无人机，并返回步骤d2，否则继续执行迭代运算。

以下以两具体实施例，验证本公开实施例提供的基于集群控制的多无人机协同目标监视控制方法的有效性：

实施例1：在本实施例中，由3个无人机组成的无人机集群其初始速度与相位角分别设定为v1＝0.3m/s，v2＝0.6m/s，v3＝0.9m/s，θ1＝0，θ2＝π/4，θ3＝π/2，所有无人机期望的最终角速度为ωc＝0.3，算法参数设定为β＝0.4，μ＝8，υ＝1.5，如图3所示，所有无人机从不同初始位置以不同初始相位出发，围绕同一个圆心做圆周运动，最终，所有无人机的相位达到同步相位分布状态。

实施例2：在本实施例中，由2个无人机组成的无人机集群其初始速度与相位角分别设定为v1＝0.3m/s，v2＝0.6m/s，θ1＝0，θ2＝π/4，所有无人机期望的最终角速度为ωc＝0.3，算法参数设定为β＝0.4，μ＝8，υ＝1.5，如图4所示，所有无人机从不同初始位置以不同初始相位出发，围绕同一个圆心做圆周运动，最终，所有无人机在实现同圆心运动的同时实现了平衡相位分布。

依据以上描述，本领域技术人员应当对本公开实施例提供的基于集群控制的多无人机协同目标监视控制方法有了清楚的认识。

综上所述，本公开提供的基于集群控制的多无人机协同目标监视控制方法通过建立目标方程，并对目标方程求取极小值，从而实现多架无人机进行协同作业，增强巡视效果并提升系统可靠性。

还需要说明的是，实施例中提到的方向用语，例如“上”、“下”、“前”、“后”、“左”、“右”等，仅是参考附图的方向，并非用来限制本公开的保护范围。贯穿附图，相同的元素由相同或相近的附图标记来表示。在可能导致对本公开的理解造成混淆时，将省略常规结构或构造。

并且图中各部件的形状和尺寸不反映真实大小和比例，而仅示意本公开实施例的内容。另外，在权利要求中，不应将位于括号之间的任何参考符号构造成对权利要求的限制。

类似地，应当理解，为了精简本公开并帮助理解各个公开方面中的一个或多个，在上面对本公开的示例性实施例的描述中，本公开的各个特征有时被一起分组到单个实施例、图、或者对其的描述中。然而，并不应将该公开的方法解释成反映如下意图：即所要求保护的本公开要求比在每个权利要求中所明确记载的特征更多的特征。更确切地说，如前面的权利要求书所反映的那样，公开方面在于少于前面公开的单个实施例的所有特征。因此，遵循具体实施方式的权利要求书由此明确地并入该具体实施方式，其中每个权利要求本身都作为本公开的单独实施例。

以上所述的具体实施例，对本公开的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本公开的具体实施例而已，并不用于限制本公开，凡在本公开的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本公开的保护范围之内。