一种基于新型二自由度内模PID的加热炉温度控制方法与流程

本发明属于自动化技术领域，涉及一种基于新型二自由度内模pid的加热炉温度控制方法。

背景技术：

在实际控制过程中，pid控制器在工业生产过程中有很高的使用率，但随着对产品的控制精度和安全操作的要求越来越高，普通的pid控制器往往不能达到要求。对于带有时滞的模型不确定/不匹配的过程，设计的控制方法往往比较复杂，又不能同时兼顾设定点跟踪特性和抗干扰特性，因此研究一种新型二自由度内模pid控制方法是有必要的。

技术实现要素：

本发明目的是针对传统的二自由度内模控制方法在工业过程生产中大时滞、控制精度不足、控制器设计复杂、模型不确定/不匹配等问题，提出了一种基于新型二自由度内模pid的加热炉温度控制方法。该方法在基于内模控制结构设计的基础上，设计了一种新的二自由度内模控制结构，采用精确的时间延迟近似方法，通过选择互补灵敏度函数以及和传统的二自由度内模控制结构等效得到二自由度的两个控制器。然后对设定点跟踪控制器的参数通过加权因子，方便整定和达到更好的设定点跟踪控制。最后通过针对一阶和二阶时滞过程采用不同的pid控制器的形式进行的控制器的等效设计，简单方便的得到控制器的各个整定参数。与传统的一些方法相比，本申请所提出的新型二自由度内模pid控制方法，能够同时实现良好的设定点跟踪和干扰抑制性能，并且设计简单，具有针对性，控制精度得到了很大的提高。

本发明方法的步骤包括：

步骤1、设计内模控制结构，具体步骤是：

1.1根据图1的传统的内模控制结构设计结构，其中，g(s)代表受控过程被控过程对象，m(s)代表过程模型，gimc(s)代表内模控制器；r表示控制系统的输入；y表示控制系统的输出；d表示干扰信号。

1.2系统输出的闭环传递函数：

1.3如果模型准确时，即g(s)＝m(s)时：

y＝gimc(s)g(s)r+[1-gimc(s)m(s)]d

可以知道，设定点跟踪特性和抗干扰抑制特性是与gimc(s)相关的。

1.4为了克服模型失配不确定性等问题，使实际控制器实现问题，利用内模控制设计过程，将过程模型分解为：

m(s)＝m+(s)m-(s)

其中，m+(s)是过程模型不可逆的部分，m-(s)是过程模型可逆的部分。

1.5选择内模控制器gimc(s)作为可逆部分的倒数，即：

1.6为了使得内模控制器合适并且可以实现，增加一个内模控制低通滤波器，低通滤波器传递函数用于使控制器稳定，设计的内模控制滤波器形式是：

其中λ是调整参数，r选择足够大以满足imc控制器合适；

1.7通过步骤1.5到1.6，内模控制器为：

1.8时间延迟部分e^-θs选择以下形式近似：

1.9通过结构转换，将图1的结构等效变换成如图2所示的经典反馈控制结构。

1.10根据等价关系，我们可以得到对控制器c(s)的设计：

步骤2、改进的二自由度内模控制结构的设计，具体步骤是：

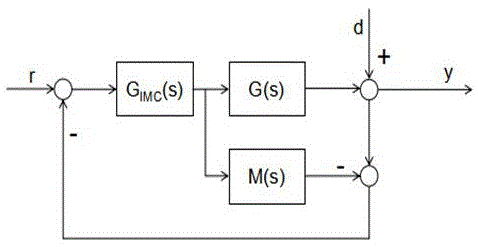
2.1二自由度内模控制结构如图3所示。q1(s)和q2(s)构成了二自由度内模控制器。

2.2从图3可以计算出控制系统输出与干扰之间的关系：

2.3过程的输入输出之间的互补灵敏度函数t(s)是：

2.4由上式可以得到控制器q2(s)：

2.5然后，进一步获得输出和干扰之间的关系：

2.6选择互补灵敏度的形式：

t(s)＝g⁺(s)h(s)

其中，λ2为待整定参数。

2.7可以得到控制器q2(s)的形式：

2.8将图3的二自由度内模控制结构图等效地转换成图4的传统二自由度内模控制结构，c1(s)和c2(s)构成了二自由度控制器。

2.9根据等价关系，可以得到：

c1(s)＝q2(s)

2.10通过计算，可以得到：

步骤3、稳定过程的控制器设计及整定，具体是：

3.1首先考虑选择λ2的值，也就是对q2(s)进行设计。为了实现更好的控制效果，我们再对λ进行调节以达到系统要求的设定点跟踪特性。

3.2在选择λ2时，在原有c2(s)的基础上增加了加权因子μ。考虑设定点控制器的设计形式如下：

其中，0≤μ≤1。μ的选择可以根据设定点的响应在[0,1]内进行在线整定，直到达到所需的设定点响应为止。

3.3考虑一阶过程模型：

其中，k是过程增益，t是过程时间常数，θ是延迟时间。

3.4在二自由度控制结构中，内模控制滤波器h(s)合理的设计为以下形式：

3.5步骤2的设计方法可以获得控制器：

改写成如下形式：

3.6将内模反馈控制器应用于pid控制器结构中：

其中，kc，ti，td分别对应于pid控制器的比例增益系数，积分增益系数和微分增益系数。

3.7通过相应的内模控制器和pid控制器的近似，可以得到：

cpid(s)＝c1(s)

即：

3.8为了简化计算，令其中，

m(s)＝0.5tθ²s³+(tθ+0.5θ²)s²+(t+θ)s+1

n(s)＝k[0.5λ2θ²s²+(λ2+0.5θ²)s+(λ2+θ)]

然后可以得到：

kc＝w'(0)

ti＝w^-1(0)

3.9根据麦克劳林展开序列可以获得各个整定参数为：

ti＝k(λ2+θ)

3.10在获得pid参数之后，有时可能需要进一步的微调以获得完美的控制器。

3.11考虑二阶时延过程模型：

其中，t1、t2为过程模型时间常数。

3.12通过将控制器形式减少到与下式的超前滞后滤波器串联的pid控制器的形式来实现pid参数：

3.13通过计算和简化，可以得到：

3.14因此，可以获得控制器的各个参数：

a＝0；b＝0.5θ²；c＝θ；d＝0

3.15在获得pid参数之后，有时可能需要进一步的微调以获得完美的控制器。

本发明提出了一种基于新型二自由度内模pid的加热炉温度控制方法。该方法改进了二自由度内模控制结构，通过对设定点跟踪控制器的参数加入加权因子，方便在线整定并达到良好的设定点跟踪，针对一阶和二阶时滞过程采用不同的pid控制器的形式进行的控制器的等效设计，简单方便的得到控制器的各个整定参数，并且能够使系统同时满足良好的跟踪性能和干扰抑制性能，系统的控制要求也能够得到保证。

附图说明

图1为内模控制框图；

图2为经典反馈控制框图；

图3为改进的二自由度内模控制结构框图；

图4为经典的二自由度控制框图；

具体实施方式

下面结合附图对本发明作进一步说明。

以实际工业加热炉炉温控制为例：

1、根据加热炉的一阶加时滞过程模型，设计二自由度内模pid控制器，具体步骤是：

1.1首先考虑工业加热炉加热过程的输入输出温度数据，建立加热炉的一阶加时滞过程模型传递函数传递函数，如下式所示：

其中，g(s)是加热炉加热过程的模型，k是过程增益系数；t是过程时间常数；θ表示延迟时间。

1.2在二自由度控制结构中，内模控制滤波器h(s)合理的设计为以下形式：

1.3根据改进的二自由度内模控制结构的设计方法可以获得控制器：

改写成如下形式：

1.4将内模反馈控制器应用于pid控制器结构中：

其中，kc，ti，td分别对应于pid控制器的比例增益系数，积分增益系数

和微分增益系数。

1.5通过相应的内模控制器和pid控制器的近似，可以得到：

cpid(s)＝c1(s)

即：

1.6为了简化计算，令其中，

m(s)＝0.5tθ²s³+(tθ+0.5θ²)s²+(t+θ)s+1

n(s)＝k[0.5λ2θ²s²+(λ2+0.5θ²)s+(λ2+θ)]

然后可以得到：

kc＝w'(0)

ti＝w^-1(0)

1.7根据麦克劳林展开序列可以获得各个整定参数为：

ti＝k(λ2+θ)

1.8在获得pid参数之后，有时可能需要进一步的微调以获得完美的控制器作用于加热炉。

2、根据加热炉的二阶加时滞过程模型，设计二自由度内模pid控制器，具体步骤是：

2.1考虑工业加热炉加热过程的输入输出温度数据，建立加热炉的二阶加时滞过程模型的传递函数，如下式所示：

其中，t1、t2为加热炉加热过程模型的时间常数。

2.2通过将控制器形式减少到与下式的超前滞后滤波器串联的pid控制器的形式来实现pid参数：

2.3通过计算和简化，可以得到：

2.4因此，可以获得控制器的各个参数：

a＝0；b＝0.5θ²；c＝θ；d＝0

2.5在获得pid参数之后，有时可能需要进一步的微调以获得完美的控制器作用于加热炉。