一种基于隐马尔科夫模型的故障容错控制方法与流程

本发明涉及一种工业过程控制和诊断
技术领域：
，尤其是涉及一种基于隐马尔科夫模型的故障容错控制方法。
背景技术：
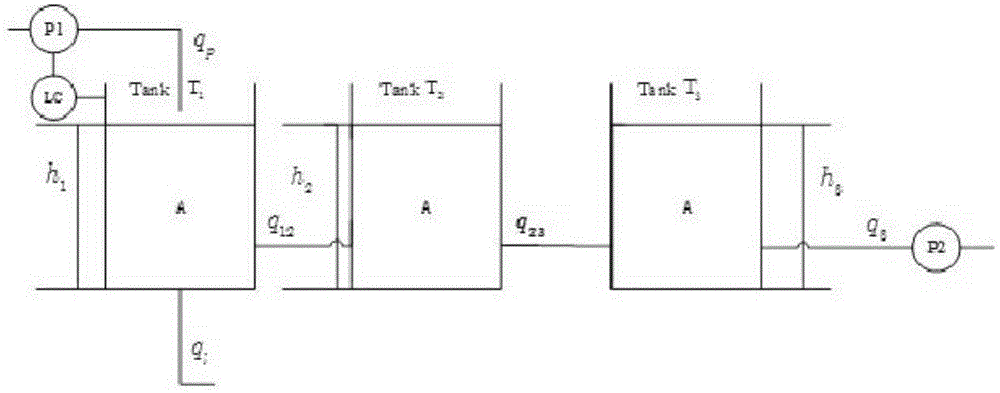
：随着工业系统日益复杂，在系统出现故障时，确保其安全、可靠和高性能运行变得越来越重要。故障容错控制方法允许通过辅助输入设计改善系统输出中故障可检测性和可隔离性。近年来，模型预测控制(modelpredictivecontrol-mpc)以其显式地处理输入输出约束而受到工业控制领域的极大关注。mpc是基于模型的控制方法，其控制效果依赖于预测模型与实际对象是否匹配。mpc算法被证明鲁棒性能良好，在一定的模型失配程度内，可以通过反馈校正达到好的动静态效果；但是，若模型出现较大程度的失配，mpc就会出现稳态误差、大的超调甚至发散。对于过程而言，噪声等外界干扰可视为小幅度模型失配现象，仅设计点mpc控制器就可达到好的控制效果；而由于物料比变化以及部件性能非正常大幅度退化等则视为大幅度模型失配。一旦故障发生，必须调整mpc控制律来保证系统安全稳定运行，并在此基础上尽可能满足较好的动态响应、较小的稳态误差。近年来的研究表明，mpc容错控制已经成功用于很多领域，即对于不同的故障选取不同的预测模型进行容错，但他们故障识别机制还是采用传统的识别方法，然后再进行相应的mpc容错处理。传统的故障识别方法往往不考虑过程变量间动态性以及可预测状态间pdf的相似性，但是实际中过程变量往往呈现极强的动态特性，且可预测状态间的pdf比较相似，那么依赖于传统故障识别方法得到的故障识别结果准确率和可靠性不高，进而导致模型预测控制的效果不佳。技术实现要素：本发明主要是解决现有技术中mpc容错控制还存在结构准确率、可靠性不高，模型预测控制效果不佳的问题，提供了一种基于隐马尔科夫模型的故障容错控制方法。本发明利用隐马尔科夫模型极强的动态过程时间序列建模能力和时序模式分类能力进行在线故障识别，且通过hellingerdistance(海林格距离)的引入提高可预测状态pdf(概率密度函数)间的差异度，从而提高故障识别的准确性和可靠性。本发明在具有强动态性工业过程发生故障的情况下，对于保证工业过程的正常运行具有更高的可靠性。本发明的上述技术问题主要是通过下述技术方案得以解决的：一种基于隐马尔科夫模型的故障容错控制方法，包括以下步骤：s1.离线建模，收集训练样本集，将工业过程采集的离线数据作为隐马尔科夫模型的观测序列，训练隐马尔科夫模型；训练样本集包括所有已知的工况，如正常工况和所有已知的故障工况。s2.在线主动容错控制，用隐马尔科夫模型对在线数据进行故障识别；s3.针对识别出的不同工况，在引入海林格距离下进行mpc容错处理。作为一种优选方案，所述步骤s1的具体过程包括：s11.用一个随机非线性系统描述工业过程，随机非线性系统采用如下公式表示：其中t是时间索引，上角标[i]表示工况索引，表示工况i的状态，nx是状态变量的数目，表示控制输入，nu是输入变量的数目，表示时不变的模型参数，nθ是模型参数的数目，表示具有已知有限协方差∑ω的零均值过程噪声，f[i]：表示工况i的模型方程，i:＝{0,…,ns}，所有工况的数目为ns+1，正常工况用i＝0表示，ns表示所有故障工况的数目；对系统状态进行检测，如下公式：yt＝xt+vt其中yt表示在t时刻被具有已知有限协方差∑v的零均值高斯测量噪声污染的测量值，xt是t时刻下系统的真实状态；则随机非线性系统中控制输入以及系统输出的约束记为以下形式：ut∈u:＝{ut|huut≤du}yt∈y:＝{yt|qyyt≤gy}其中nc是输入约束的数目，nd是输出约束的数目；s12.收集训练样本集，包括所有已知工况i:＝{0,1，…,ns}，已知工况为正常工况和所有已知的故障工况；s13.将采集的训练样本集作为观测向量，用于训练隐马尔科夫模型，得到模型参数λ＝(a,b,π,m,n)；其中a是隐含状态转移概率矩阵，b是观测值概率密度矩阵，π是初始状态概率矩阵，m是每个隐含状态下的高斯混合成分的数目，n是隐含状态的数目，这里隐含状态的数目就是训练样本集中所有工况的数目，即n＝ns+1；a是隐含状态转移概率矩阵，描述了hmm模型中各个状态之间的转移概率，其公式为：其中简记为ai,j，表示在t时刻，隐含状态为si的条件下，在t+1时刻隐含状态是sj的概率；b是观测值概率密度矩阵，计算如下式b＝{bj(o),j＝1,2,…n}其中o是观测向量，cjm是隐含状态j的第m个混合成分的混合系数，h是对数凹或椭圆对称密度，μjm是隐含状态的第m个混合成分的均值向量，ujm是隐含状态sj的第m个混合成分的协方差矩阵，cjm满足随机约束：其中αt(j)＝p(o1,o2,…,ot,qt＝sj|λ)表示在给定模型参数λ＝(a,b,π,m,n)条件下，t时刻下隐含状态为sj且观测序列为o1,o2,…,ot的概率；βt(j)＝p(ot+1,ot+2,…,ot|qt＝sj,λ)表示在给定模型参数λ＝(a,b,π,m,n)和t时刻下隐含状态qt＝sj的条件下，从t+1到t时刻观测序列为ot+1,ot+2,…,ot的概率；是cjk的估计值，是μjk的估计值，是ujk的估计值。作为一种优选方案，所述步骤s2的具体过程包括：s21.在线采集工业过程的数据；s22.对采集到的样本点yt，利用训练好的隐马尔科夫模型计算其属于各个工况的后验概率p(st|yt,λ)，即获得{p(st＝1|yt,λ)，p(st＝2|yt,λ)，…，p(st＝n|yt,λ)}；s23.后验概率{p(st＝1|yt,λ)，p(st＝2|yt,λ)，…，p(st＝n|yt,λ)}中最大的值为p*，p*所对应的工况为st*，判断样本点yt此时处于工况st*。作为一种优选方案，所述步骤s3的具体过程包括：s31.判断当前样本所属工况后，进行mpc容错处理，mpc的二次目标函数表示如下：s.t.ut+i∈u:＝{ut+i|huut+i≤du}i＝0,1,…,l-1yt+i∈y:＝{yt+i|qyyt+i≤gy}i＝1,…,l其中et＝rt-yt，rt是跟踪参考输出向量，et+i与δut+i表示自当前时刻起未来i步的跟踪误差及控制输入变化量，λ是控制量权系数，l表示有限时域长度，u，y分别为输入输出量的约束限制；mpc是一种在控制规律推导开始时就显示地并入约束的一种技术，这种处理约束的能力来自其基于模型对系统未来动态行为的预测，可以把约束显示表示在一个在线求解的二次规划问题中，即将约束并入mpc优化算法中。s32.将海林格距离引入到二次目标函数中，使用dh来量化两个pdf之间的距离，对于下一个时刻所有状态，两个工况i1和i2的各个组合对计算如下：其中三重求和将所有状态对的海林格距离加在一起，是t时刻对工况i的t+1时刻第m个状态的估计值，当概率分布之间无法分离时，即它们的pdf完全相同，dh＝0；当分布之间没有重叠时，dh＝1；hellinger距离即海林格距离是用于量化两个概率分布之间的相似性，为了增大可预测状态pdf(概率密度函数)间的差异度。上述各个组合对计算公式中的dh对于任何观测测量值yt确保了其最优预测模型模糊度的降低，这使得能够增加随机非线性系统公式中不同工况相对应的后验概率p(st|yt,λ)的准确度。二次目标优化函数变为以下形式：s.t.ut+i∈u:＝{ut+i|huut+i≤du}i＝0,1,…,l-1yt+i∈y:＝{yt+i|qyyt+i≤gy}i＝1,…,l其中第一项和第二项是由控制带来的代价函数，第三项是引入的海林格距离。因此，本发明的优点是：1.基于隐马尔科夫模型的故障容错控制方法，实现对工业过程的容错控制；通过hellingerdistance(海林格距离)的引入提高可预测状态pdf(概率密度函数)间的差异度，从而提高故障识别的准确性和可靠性。2.能够解决过程数据存在的动态性，从而能够更有效地进行容错控制；在具有强动态性工业过程发生故障的情况下，对于保证工业过程的正常运行具有更高的可靠性。3.能够解决可预测状态间概率密度函数的相似性，从而能够更有效地进行容错控制。附图说明图1是本发明中实施例三阶水槽系统的一种原理示意图。具体实施方式下面通过实施例，并结合附图，对本发明的技术方案作进一步具体的说明。实施例：本实施例一种基于隐马尔科夫模型的故障容错控制方法，包括以下步骤：s1.离线建模，收集训练样本集，将工业过程采集的离线数据作为隐马尔科夫模型的观测序列，训练隐马尔科夫模型；具体过程包括：s11.用一个随机非线性系统描述工业过程，随机非线性系统采用如下公式表示：其中t是时间索引，上角标[i]表示工况索引，表示工况i的状态，nx是状态变量的数目，表示控制输入，nu是输入变量的数目，表示时不变的模型参数，nθ是模型参数的数目，表示具有已知有限协方差∑ω的零均值过程噪声，f[i]：表示工况i的模型方程，i:＝{0,…,ns}，所有工况的数目为ns+1，正常工况用i＝0表示，ns表示所有故障工况的数目；对系统状态进行检测，如下公式：yt＝xt+vt其中yt表示在t时刻被具有已知有限协方差∑v的零均值高斯测量噪声污染的测量值，xt是t时刻下系统的真实状态；则随机非线性系统中控制输入以及系统输出的约束记为以下形式：ut∈u:＝{ut|huut≤du}yt∈y:＝{yt|qyyt≤gy}其中nc是输入约束的数目，nd是输出约束的数目；s12.收集训练样本集，包括所有已知工况i:＝{0,1，…,ns}，已知工况为正常工况和所有已知的故障工况；s13.将采集的训练样本集作为观测向量，用于训练隐马尔科夫模型，得到模型参数λ＝(a,b,π,m,n)；其中a是隐含状态转移概率矩阵，b是观测值概率密度矩阵，π是初始状态概率矩阵，m是每个隐含状态下的高斯混合成分的数目，n是隐含状态的数目，这里隐含状态的数目就是训练样本集中所有工况的数目，即n＝ns+1；a是隐含状态转移概率矩阵，描述了隐马尔科夫模型中各个状态之间的转移概率，其公式为：其中简记为ai,j，表示在t时刻，隐含状态为si的条件下，在t+1时刻隐含状态是sj的概率；b是观测值概率密度矩阵，计算如下式b＝{bj(o),j＝1,2,…n}其中o是观测向量，cjm是隐含状态j的第m个混合成分的混合系数，h是对数凹或椭圆对称密度，μjm是隐含状态的第m个混合成分的均值向量，ujm是隐含状态sj的第m个混合成分的协方差矩阵，cjm满足随机约束：cjm≥0,1≤j≤n,1≤m≤mcjm、μjm、ujm的重估为：cjm的重估值是隐马尔科夫模型在隐含状态sj带有第k个混合成分的次数的期望除以隐马尔科夫模型处于隐含状态sj的次数的期望，μjm的重估值是由第k个混合成分说明的观测矢量的部分期望值，ujm是由第k个混合成分说明的观测矢量的部分协方差，如以下公式：其中αt(j)＝p(o1,o2,…,ot,qt＝sj|λ)表示在给定模型参数λ＝(a,b,π,m,n)条件下，t时刻下隐含状态为sj且观测序列为o1,o2,…,ot的概率；βt(j)＝p(ot+1,ot+2,…,ot|qt＝sj,λ)表示在给定模型参数λ＝(a,b,π,m,n)和t时刻下隐含状态qt＝sj的条件下，从t+1到t时刻观测序列为ot+1,ot+2,…,ot的概率；是cjk的估计值，是μjk的估计值，是ujk的估计值。s2.在线主动容错控制，用隐马尔科夫模型对在线数据进行故障识别；具体过程包括：s21.在线采集工业过程的数据；s22.对采集到的样本点yt，利用训练好的隐马尔科夫模型计算其属于各个工况的后验概率p(st|yt,λ)，即获得{p(st＝1|yt,λ)，p(st＝2|yt,λ)，…，p(st＝n|yt,λ)}；s23.后验概率{p(st＝1|yt,λ)，p(st＝2|yt,λ)，…，p(st＝n|yt,λ)}中最大的值为p*，p*所对应的工况为st*，判断样本点yt此时处于工况st*。s3.针对识别出的不同工况，在引入海林格距离下进行mpc容错处理。具体过程包括：s31.判断当前样本所属工况后，进行mpc容错处理，mpc的二次目标函数表示如下：s.t.ut+i∈u:＝{ut+i|huut+i≤du}i＝0,1,…,l-1yt+i∈y:＝{yt+i|qyyt+i≤gy}i＝1,…,l其中et＝rt-yt，rt是跟踪参考输出向量，et+i与δut+i表示自当前时刻起未来i步的跟踪误差及控制输入变化量，λ是控制量权系数，l表示有限时域长度，u，y分别为输入输出量的约束限制；mpc是一种在控制规律推导开始时就显示地并入约束的一种技术，这种处理约束的能力来自其基于模型对系统未来动态行为的预测，可以把约束显示表示在一个在线求解的二次规划问题中，即将约束并入mpc优化算法中。s32.将海林格距离引入到二次目标函数中，使用dh来量化两个pdf之间的距离，对于下一个时刻所有状态，两个工况i1和i2的各个组合对计算如下：其中三重求和将所有状态对的海林格距离加在一起，是t时刻对工况i的t+1时刻第m个状态的估计值，当概率分布之间无法分离时，即它们的pdf完全相同，dh＝0；当分布之间没有重叠时，dh＝1；hellinger距离即海林格距离是用于量化两个概率分布之间的相似性，为了增大可预测状态pdf(概率密度函数)间的差异度。上述各个组合对计算公式中的dh对于任何观测测量值yt确保了其最优预测模型模糊度的降低，这使得能够增加随机非线性系统公式中不同工况相对应的后验概率p(st|yt,λ)的准确度。二次目标优化函数变为以下形式：s.t.ut+i∈u:＝{ut+i|huut+i≤du}i＝0,1,…,l-1yt+i∈y:＝{yt+i|qyyt+i≤gy}i＝1,…,l其中第一项和第二项是由控制带来的代价函数，第三项是引入的海林格距离。以下采用一个具体的例子进行说明，在一个三阶水槽系统中使用本实施例的方法。液位控制是工业生产中典型的过程控制问题，对液位进行准确的测量和有效控制是一些设备优质高产、低耗和安全生产的重要指标。三阶水槽系统原理如图1所示。三个水槽具有完全相同的横截面积a，液体以流量qp流入水槽t1，中间由管道连接且液体流量分别为q12和q23，水槽t3的液体流出量为q3。系统正常运行工况记作m[0]，故障工况m[1]表示水槽t1发生泄漏且所泄漏流量为ql，故障工况m[2]表示水槽t1和水槽t2之间的管道发生堵塞，故障工况m[3]表示水槽t1的泵性能发生损失，系统可表示如下：其中系统模型的参数如下所示：abclc12c23c3∑ω130.11110.1接下来结合该具体过程对本发明的步骤进行详细阐述：步骤s1.离线建模，收集训练样本集，将工业过程采集的离线数据作为隐马尔科夫模型的观测序列，训练隐马尔科夫模型；s11.离线建模系统模型如公式(1)表示：系统状态即水槽液位，x1:＝h1，x2:＝h2以及x3:＝h3。过程噪声表示具有已知有限协方差∑ω的零均值过程噪声，控制目标是保证第一个水槽的液位在它的参考值。所有状态都是可测的，yt表示在t时刻被具有已知有限协方差∑v的零均值高斯测量噪声污染的测量值，具体如下所示：yt＝xt+vt其中xt是t时刻下系统的真实状态。公式(1)中控制输入、输出的约束可记为如下形式：ut∈u:＝{ut|huut≤du}yt∈y:＝{yt|qyyt≤gy}其中nc是输入约束的数目，nd是输出约束的数目。s12.收集训练样本集，包括所有已知工况，已知工况包括正常工况和3种已知的故障工况：水槽t1的泄漏，水槽t1和水槽t2之间的管道堵塞以及水槽t1的泵性能损失。s13.将采集的训练样本集作为观测向量，用于训练隐马尔科夫模型，得到模型参数λ＝(a,b,π,m,n)；其中a是隐含状态转移概率矩阵，b是观测值概率密度矩阵，π是初始状态概率矩阵，m是每个隐含状态下的高斯混合成分的数目，n是隐含状态的数目，这里隐含状态的数目就是训练样本集中所有工况的数目，即n＝ns+1；为了计算推导的简洁，下面隐含状态的数目用n表示。a是隐含状态转移概率矩阵，描述了隐马尔科夫模型中各个状态之间的转移概率，其公式为：其中简记为ai,j，表示在t时刻，隐含状态为si的条件下，在t+1时刻隐含状态是sj的概率；b是观测值概率密度矩阵，计算如下式b＝{bj(o),j＝1,2,…n}其中o是观测向量，cjm是隐含状态j的第m个混合成分的混合系数，h是对数凹或椭圆对称密度，μjm是隐含状态的第m个混合成分的均值向量，ujm是隐含状态sj的第m个混合成分的协方差矩阵，cjm满足随机约束：cjm≥0,1≤j≤n,1≤m≤mcjm、μjm、ujm的重估为：cjm的重估值是隐马尔科夫模型在隐含状态sj带有第k个混合成分的次数的期望除以隐马尔科夫模型处于隐含状态sj的次数的期望，μjm的重估值是由第k个混合成分说明的观测矢量的部分期望值，ujm是由第k个混合成分说明的观测矢量的部分协方差，如以下公式：其中αt(j)＝p(o1,o2,…,ot,qt＝sj|λ)表示在给定模型参数λ＝(a,b,π,m,n)条件下，t时刻下隐含状态为sj且观测序列为o1,o2,…,ot的概率；βt(j)＝p(ot+1,ot+2,…,ot|qt＝sj,λ)表示在给定模型参数λ＝(a,b,π,m,n)和t时刻下隐含状态qt＝sj的条件下，从t+1到t时刻观测序列为ot+1,ot+2,…,ot的概率；是cjk的估计值，是μjk的估计值，是ujk的估计值。s2.在线主动容错控制，用隐马尔科夫模型对在线数据进行故障识别；s21.在线采集工业过程的数据；s22.对采集到的样本点yt，利用训练好的隐马尔科夫模型计算其属于各个工况的后验概率p(st|yt,λ)，即获得{p(st＝1|yt,λ)，p(st＝2|yt,λ)，…，p(st＝n|yt,λ)}；s23.后验概率{p(st＝1|yt,λ)，p(st＝2|yt,λ)，…，p(st＝n|yt,λ)}中最大的值为p*，p*所对应的工况为st*，判断样本点yt此时处于工况st*。s3.针对识别出的不同工况，在引入海林格距离下进行mpc容错处理。s31.判断当前样本所属工况后，进行mpc容错处理，mpc是一种在控制规律推导开始时就显示地并入约束的一种技术，这种处理约束的能力来自其基于模型对系统未来动态行为的预测，可以把约束显示表示在一个在线求解的二次规划问题中，即将约束并入mpc优化算法中。为了获得最优输出轨迹，mpc的二次目标函数表示如下：s.t.ut+i∈u:＝{ut+i|huut+i≤du}i＝0,1,…,l-1yt+i∈y:＝{yt+i|qyyt+i≤gy}i＝1,…,l其中et＝rt-yt，rt是跟踪参考输出向量，et+i与δut+i表示自当前时刻起未来i步的跟踪误差及控制输入变化量，λ是控制量权系数，l表示有限时域长度，u，y分别为输入输出量的约束限制；s32.将海林格距离引入到二次目标函数中，(hellinger距离即海林格距离是用于量化两个概率分布之间的相似性)，使用dh来量化两个pdf之间的距离，对于下一个时刻所有状态，两个工况i1和i2的各个组合对计算如下：其中三重求和将所有状态对的海林格距离加在一起，是t时刻对工况i的t+1时刻第m个状态的估计值，当概率分布之间无法分离时，即它们的pdf完全相同，dh＝0；当分布之间没有重叠时，dh＝1；为了增大可预测状态pdf(概率密度函数)间的差异度。上述各个组合对计算公式中的dh对于任何观测测量值yt确保了其最优预测模型模糊度的降低，这使得能够增加随机非线性系统公式中不同工况相对应的后验概率p(st|yt,λ)的准确度。二次目标优化函数变为以下形式：s.t.ut+i∈u:＝{ut+i|huut+i≤du}i＝0,1,…,l-1yt+i∈y:＝{yt+i|qyyt+i≤gy}i＝1,…,l其中第一项和第二项是由控制带来的代价函数，第三项是引入的海林格距离。目的在于提高公式(1)中模型间可预测状态pdf(概率密度函数)间的差异度，rh是一个标量权重。本文中所描述的具体实施例仅仅是对本发明精神作举例说明。本发明所属
技术领域：
的技术人员可以对所描述的具体实施例做各种各样的修改或补充或采用类似的方式替代，但并不会偏离本发明的精神或者超越所附权利要求书所定义的范围。当前第1页12