本发明涉及系统的控制,更具体地,涉及使用具有不确定性的系统动力学模型来控制系统。
背景技术:
许多高级控制技术被表述为优化问题,其可由控制系统实时求解。基于描述系统动力学的模型的类型,一些系统通常被称为线性或非线性系统。例如,线性系统是基于线性算子的使用的系统模型。线性系统通常表现出远比非线性情况更简单的特征和性质,并在自动控制理论、信号处理和电信中获得重要应用。例如,无线通信系统的传播介质常常可通过线性系统建模,并且在驾驶者和/或控制系统的特定条件下,道路车辆的运动可由线性系统描述。
基于模型的控制的性能不可避免地取决于用于最优控制计算的预测模型的质量。然而,在许多应用中,受控系统的模型部分未知或不确定。在这样的情况下,对不确定模型施加控制可导致非最优的性能或者甚至受控系统的不稳定性。
卡尔曼滤波器(kf)是在线性状态空间模型中进行状态估计的标准工具。状态可与动力学系统的物理变量(例如,位置、速度、取向、其组合或流动)有关,但是如果使用黑箱估计模型获得了模型的话也可以是非物理的。从最小方差意义上讲它是最佳线性无偏滤波器,对于高斯噪声,它是最优贝叶斯滤波器。kf是传播状态估计的均值和方差的实时递归方法,对于已知高斯噪声,其是估计系统的全概率分布所需的信息(充分统计)的量。kf的经典表述假设噪声过程是高斯的并且具有已知均值和协方差,这会是苛刻限制。
模型不确定性和可能的数据异常值影响kf的性能,并且在许多实际情况下,模型参数是未知的或者至少不确定。例如,在使用惯性感测和/或gps的导航系统中,噪声统计常常具有时间相关性,其无法先验地确定。其它示例是由于近似非线性模型中的线性化误差而引起的噪声统计变化、环境相关传感器统计以及不可靠传感器中的异常值,高斯分布由于在尾部中的低概率质量而对其处理不足。噪声参数决定模型的不同部分的可靠性,因此对于滤波器性能而言特别重要。然而,实践中常常进行的噪声参数的手动调整会是极具挑战性、耗时且繁琐的任务。
由于噪声参数估计的精确方法不可行,所以设计了近似方法。例如,us7209938b2中所描述的方法公开了与方差估计器组合的kf,以估计动力学系统的状态以及关联的测量噪声的方差。然而,此方法对异常值敏感,这在基于gps/惯性感测的估计系统中(但不限于此)是常见情况。
其它方法基于增强状态向量以包括模型的不确定性的参数,例如噪声的均值和方差。然而,因为状态向量比其需要的大,所以这种方法导致估计问题不必要地复杂。此外,这种方法依赖于引入参数的动力学演进模型,这实际上是未知的。
因此,需要使用包括不确定性的系统动力学模型对系统进行基于模型的控制。
技术实现要素:
通常,系统的模型包括两个模型(方程)。第一模型是系统的运动模型,其将系统的状态与系统的先前状态和系统的输入相关联。运动模型通常包括表示运动模型的不确定性的噪声或扰动。该不确定性在本文中称为过程噪声。第二模型是测量模型,其将系统的可用测量与系统的状态相关联。测量模型也包括测量噪声和/或其它不确定性,其在本文中称为测量噪声。
运动模型的示例是xk+1=axk+wk,其中,wk是过程噪声。另外,测量模型的示例是yk=cxk+ek,其中,ek是测量噪声。
另外,系统的状态也受不确定性影响,本文中称为状态不确定性。特别是,过程噪声和测量噪声导致状态不确定性,然而,状态不确定性不同于过程噪声和测量噪声。具体地,状态不确定性是状态值内部的,而过程噪声和测量噪声是对状态的外部扰动。
当过程噪声和测量噪声已知,即,过程噪声和测量噪声的分布的形状和参数已知时,各种技术允许估计系统的状态和状态不确定性二者。系统的状态和状态不确定性二者对于许多控制应用而言是重要的。例如,系统的状态可用于确定对系统的控制输入以实现控制目标,而状态不确定性可用于调节控制输入以确保控制的可行性。
例如,当过程噪声和测量噪声的分布为高斯的,并且过程噪声和测量噪声的高斯分布的均值和方差已知时,可使用卡尔曼滤波器来估计系统的状态和状态不确定性二者。然而,当过程噪声和测量噪声中的至少一个的高斯分布的方差未知时,卡尔曼滤波器不适用。为此,对于许多控制应用而言知道过程噪声和测量噪声的分布的或然性参数是有益的。
一些实施方式基于这样的理解:可利用平均期望值来表示未知或然性参数。然而,在许多情况下,或然性参数随时间变化,使用平均期望值将导致或然性参数具有恒定值,这不是最优的。
为此,需要作为时间的函数来估计过程噪声和测量噪声中的至少一个或组合的分布的或然性参数的系统和方法。
一些实施方式基于这样的认识:当分布的或然性参数未知时,假设分布是高斯分布是合理的。例如,该假设被大数定律证明是正确的。例如,加速度计具有高频噪声分量,当以固定采样率测量时其类似高斯概率分布。
一些实施方式基于另一认识:可估计高斯分布的未知或然性参数,例如均值和方差。例如,由于高斯分布的对称性,可使用数据样本的变化的平均来估计高斯分布的方差。
然而,一些实施方式基于这样的认识:当过程噪声和/或测量噪声的高斯分布的方差未知时,过程噪声和/或测量噪声的分布应该是student-t分布,即使过程噪声和/或测量噪声的实际分布为高斯的。这是因为,student-t分布可更好捕获高斯分布的未知方差的不确定性。然而,不幸的是,student-t分布不适合于许多控制方法。即,如果以student-t分布来表示系统的状态,则将违反设计控制方法时的许多假设。例如,诸如线性二次高斯控制器(lqg)的许多控制系统依赖于过程噪声和测量噪声的高斯假设来提供稳定性保证。
为此,一些实施方式在高斯分布和student-t分布之间执行多个变换以捕获过程的高斯性质和高斯性质的不确定性二者。这种变换允许在未被设计为考虑student-t分布的各种控制方法中考虑高斯分布的不确定性。例如,一个实施方式确定高斯噪声的均值和方差的初始估计,从而将student-t分布的参数拟合到高斯分布。另一实施方式迭代地估计student-t分布的参数(即,均值、比例和自由度),并将高斯分布拟合到student-t分布。这样做导致符合高斯噪声假设,但仍考虑了高斯分布的均值和方差的不确定性。
随着时间流逝,student-t分布接近高斯分布。一个实施方式基于这样的理解:避免这种合并会是有益的。因此,该实施方式限制student-t分布的参数,使得student-t和高斯彼此充分靠近,但不完全相同。
一些实施方式基于这样的理解:各个时间步中的动力学系统的状态可通过类似于kf的解析表达式来更新。
其它实施方式认识到,可通过测量与测量的状态估计之差来更新参数。一个实施方式以状态估计的不确定性对测量与测量的状态估计之差进行加权,以进一步考虑到状态估计的知识是不确定的。
其它实施方式认识到,在测量包含关于动力学系统(具有噪声相关性的系统)的扰动的信息的情况下,预测动力学模型的状态可使用来自先前时间步的测量来完成。还认识到,使用先前测量来预测状态导致参数的更新可保留,但仍包含关于噪声相关性的信息。例如,这种方法对于汽车应用而言是有益的,其中来自驾驶者的转向输入是对车辆的运动模型的输入,从而影响车辆的速度。转向输入不完全已知,而是由附接到车辆的方向盘的噪声传感器测量。如果使用惯性测量(例如,加速度测量),则车辆的测量模型也包括来自驾驶者的转向输入。因此,车辆的测量模型中包含关于转向输入的信息。
因此,一个实施方式基于这样的理解:影响系统的运动模型的传感器和影响系统的测量模型的传感器常常受传感器测量的变化的知识的不确定性和时变偏移影响。另一实施方式基于传感器可由确定性部分和随机性部分的组合来建模,其中随机性部分由具有未知均值和方差的高斯分布来建模。各种实施方式认识到,高斯分布的均值和方差可用于对传感器测量的偏移和变化进行建模。因此,在一个实施方式中,通过确定高斯扰动的均值和方差来校准传感器。
因此,一个实施方式公开了一种用于控制系统的设备,该设备包括:存储器,其存储系统的模型,该模型包括系统的受过程噪声影响的运动模型以及系统的受测量噪声影响的测量模型,使得过程噪声和测量噪声中的一个或组合形成具有未知或然性参数的系统模型的不确定性,其中,系统模型的不确定性导致具有未知或然性参数的系统的状态不确定性;传感器,其测量信号以生成指示系统的状态的一系列测量;处理器,其使用系统的状态的测量、运动模型和测量模型中的至少一个或组合来估计表示模型的不确定性的第一student-t分布和表示系统的状态不确定性的第二student-t分布,该估计迭代地执行,直至满足终止条件为止;并将表示状态不确定性的高斯分布拟合为第二student-t分布;以及控制器,其使用具有由高斯分布表示的状态不确定性的系统模型来确定对系统的控制输入;并根据控制输入来控制系统。
另一实施方式公开了一种控制系统的方法,其中,该方法使用与所存储的实现该方法的指令联接的处理器,其中,所述指令在由处理器执行时执行该方法的步骤,这些步骤包括:检索系统的模型,该模型包括系统的受过程噪声影响的运动模型以及系统的受测量噪声影响的测量模型,使得过程噪声和测量噪声中的一个或组合形成具有未知或然性参数的系统模型的不确定性,其中,系统模型的不确定性导致具有未知或然性参数的系统的状态不确定性;接收指示系统的状态的一系列测量;使用系统的状态的测量、运动模型和测量模型中的至少一个或组合来估计表示模型的不确定性的第一student-t分布和表示系统的状态不确定性的第二student-t分布,其中,该估计迭代地执行,直至满足终止条件为止;将表示状态不确定性的高斯分布拟合为第二student-t分布;使用具有由高斯分布表示的状态不确定性的系统模型来确定对系统的控制输入;以及根据控制输入来控制系统。
另一实施方式公开了一种具体实现有程序的非暂时性计算机可读存储介质,该程序可由处理器执行以用于执行一种方法,该方法包括:检索系统的模型,该模型包括系统的受过程噪声影响的运动模型以及系统的受测量噪声影响的测量模型,使得过程噪声和测量噪声中的一个或组合形成具有未知或然性参数的系统模型的不确定性,其中,系统模型的不确定性导致具有未知或然性参数的系统的状态不确定性;接收指示系统的状态的一系列测量;使用系统的状态的测量、运动模型和测量模型中的至少一个或组合来估计表示模型的不确定性的第一student-t分布和表示系统的状态不确定性的第二student-t分布,其中,该估计迭代地执行,直至满足终止条件为止;将表示状态不确定性的高斯分布拟合为第二student-t分布;使用具有由高斯分布表示的状态不确定性的系统模型来确定对系统的控制输入;以及根据控制输入来控制系统。
附图说明
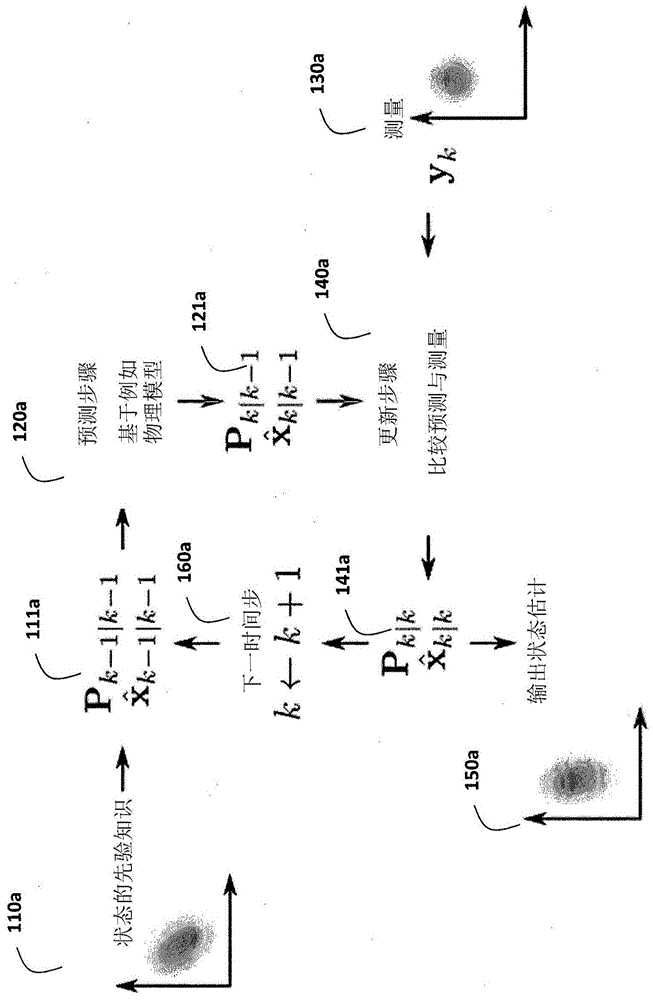
[图1a]图1a是示出根据一些实施方式的原理的例示。
[图1b]图1b是高斯分布的例示。
[图1c]图1c是对于不同的自由度,student-t分布如何变化的例示。
[图1d]图1d是根据一些实施方式的高斯分布如何不太适合于处理或然性参数中的不确定性的例示。
[图1e]图1e是根据一些实施方式的student-t分布如何适合于处理或然性参数中的不确定性的例示。
[图2a]图2a是根据本发明的一个实施方式的联合估计系统的状态和系统的或然性参数以控制系统的方法的流程图。
[图2b]图2b是根据一个实施方式的确定初始估计的示例实现方式的流程图。
[图2c]图2c是根据一些实施方式的用于控制系统的设备的框图。
[图3a]图3a示出更新系统的状态的方法的一个迭代的流程图。
[图4a]图4a是根据本发明的一些实施方式的确定系统的或然性参数和状态的例示。
[图4b]图4b是根据本发明的一些实施方式的确定系统的或然性参数和状态的例示。
[图4c]图4c是根据本发明的一些实施方式所采用的一些原理确定的不同运动的示意图。
[图4d]图4d是根据本发明的一些实施方式所采用的一些原理确定的不同运动和关联的概率分布的示意图。
[图5a]图5a是传感器的传感器测量通常如何随时间变化的例示。
[图5b]图5b是传感器的传感器偏移如何随传感器的放置变化的例示。
[图5c]图5c是传感器的传感器方差如何随传感器的放置变化的例示。
[图6a]图6a示出根据本发明的一个实施方式的通过联合估计系统的状态和系统的传感器的状态来控制系统的方法的流程图。
[图6b]图6b示出例示了定义传感器状态的可行空间的概率分布函数的曲线图。
[图6c]图6c示出根据迭代地更新粒子的一个实施方式的更新粒子的方法的一个迭代的框图。
[图7a]图7a示出根据一个实施方式的控制系统的一般框图。
[图7b]图7b示出根据一个实施方式的传感器状态估计器的一般结构。
具体实施方式
通常,系统的模型包括两个模型(方程)。第一模型是系统的运动模型,其将系统的状态与系统的先前状态和系统的输入相关联。例如,模型可以是在道路上行驶的运动模型,其中系统的状态包括速度和航向角速度,并且其中系统的输入是驾驶者的转向角。运动模型通常包括表示运动模型的不确定性的噪声或扰动。例如,扰动可表示车辆的驾驶者的行为的不确定性。该不确定性在本文中称为过程噪声。第二模型是测量模型,其将系统的可用测量与系统的状态相关联。例如,测量可以是将加速度测量与车辆的速度相关联的加速度计。测量模型也包括测量噪声和/或其它不确定性,在本文中称为测量噪声。例如,由于各种来源(例如,加速度计的组件中的机械振动),加速度计的测量中有噪声。
运动模型的示例是xk+1=akxk+wk,其中,wk是过程噪声,xk是状态。测量模型的示例是yk=ckxk+ek,其中,ek是测量噪声。
运动模型和测量中的不确定性导致状态的知识也具有不确定性,这通常不是与过程噪声和/或测量噪声相同的噪声。
图1a示出一些实施方式所使用的卡尔曼滤波器(kf)的示意图。kf是在线性状态空间模型中进行状态估计的工具,当噪声源已知并且为高斯的时它是最优估计器,在这种情况下状态估计也是高斯分布的。kf估计高斯分布的均值和方差,因为均值和方差是描述高斯分布所需的两个量(充分统计)。
图1b示出在使用图1a的kf时一些实施方式所使用的高斯分布110b的草图。高斯分布110b以分布的均值120b为中心,并且方差130b测量分布的宽展(宽度)。返回参照图1a,kf以状态的初始知识110a开始,以确定状态的均值及其方差111a。然后,kf使用系统的模型来预测120a到下一时间步的状态和方差,以获得状态的更新的均值和方差121a。然后,kf在更新步骤140a中使用系统的测量模型使用测量130a,以确定状态的更新的均值和方差141a。然后获得输出150a,并且针对下一时间步160a重复该过程。
图1c示出例示了对于student-t分布中的变化自由度,高斯分布与student-t分布之间的差异的曲线图。高斯分布的均值120b和方差130b足以描述形状。student-t分布需要三个参数,均值、比例和自由度。比例是利用取决于自由度的函数缩放的方差。例如,图1c示出具有三个不同的自由度的三个student-t形状。对于自由度的数量较少,student-t分布130c是高斯的平滑版本。然而,随着自由度的数量增加,student-t变得更类似于高斯分布(120c和110c)。
系统的状态和状态不确定性二者对于许多控制应用而言是有用的。例如,系统的状态可用于确定对系统的控制输入以实现控制目标,而状态不确定性可用于调节控制输入以确保控制的可行性。
当过程噪声和测量噪声的分布为高斯的,并且过程噪声和测量噪声的高斯分布的均值和方差已知时,可使用kf来估计系统的状态和状态不确定性二者。然而,当过程噪声和测量噪声中的至少一个的高斯分布的方差未知时,kf不适用。为此,对于许多控制应用而言知道过程噪声和测量噪声的分布的或然性参数是有益的。例如,对于高斯噪声,或然性参数包括产生噪声的高斯分布的均值和方差。
一些实施方式基于这样的认识:当分布的或然性参数未知时,假设分布为高斯分布是合理的。例如,该假设被大数定律证明是正确的。例如,加速度计具有高频噪声分量,当以固定采样率测量时其类似于高斯概率分布。
一些实施方式基于另一认识:可估计高斯分布的未知或然性参数,例如均值和方差。例如,由于高斯分布的对称性,可使用数据样本的变化的平均来估计高斯分布的方差。然而,一些实施方式基于这样的认识:当过程噪声和/或测量噪声的高斯分布的方差未知时,过程噪声和/或测量噪声的分布应该是student-t分布,即使过程噪声和/或测量噪声的实际分布是高斯的。这是因为student-t分布可更好捕获高斯分布的未知方差的不确定性。
图1d示出高斯分布110d和测量120d,其中高斯分布110d的或然性参数未知,并且测量120d源自110d。测量120d不靠近110d的中心,但发生的概率不可忽略。然而,测量120d被建模为源自高斯分布130d,以130d的或然性参数的当前估计,该测量具有接近零的概率,并且结果将是状态估计器将以错误的方式移动与120d关联的状态估计和分布140d。
图1e示出高斯分布110d和测量120d,其中高斯分布110d的或然性参数未知,并且测量120d源自110d。测量120d不靠近110d的中心,但发生的概率不可忽略。然而,测量120d在估计器中被建模为源自student-t分布130e,因为student-t130e的尾部覆盖测量120d,所以该测量具有非零概率,并且结果是状态估计器以更好的方式移动状态估计和分布140e。
然而,不幸的是,student-t分布不适合于许多控制方法。即,如果以student-t分布来表示系统的状态,则将违反设计控制方法时的许多假设。例如,诸如线性二次高斯控制器(lqg)的许多控制系统依赖于过程噪声和测量噪声的高斯假设来提供稳定性保证。
为此,一些实施方式在高斯分布和student-t分布之间执行多个变换以捕获过程的高斯性质和高斯性质的不确定性二者。这种变换允许在未被设计为考虑student-t分布的各种控制方法中考虑高斯分布的不确定性。
例如,一个实施方式确定高斯噪声的均值和方差的初始估计,从而将student-t分布的参数拟合到高斯分布。另一实施方式迭代地估计student-t分布的参数(即,均值、比例和自由度),并将高斯分布拟合到student-t分布。这样做导致符合高斯噪声假设,但仍考虑了高斯分布的均值和方差的不确定性。
图2a示出根据系统的模型来控制系统的方法的流程图,该模型包括系统的受过程噪声影响的运动模型以及系统的受测量噪声影响的测量模型,使得过程噪声和测量噪声中的一个或组合形成具有未知或然性参数的系统模型的不确定性,其中,系统模型的不确定性导致具有未知或然性参数的系统的状态不确定性。例如,未知或然性参数可以是高斯分布的均值和方差。例如,系统的参数(例如,质量)可被建模为具有统计均值和方差的高斯扰动。
为此,该方法确定表示模型的不确定性的第一高斯分布的均值和方差的初始估计210a,以生成第一高斯分布的均值和方差215a。然后,该方法使用均值和方差215a来将第一student-t分布拟合到具有均值和方差的初始值的高斯分布,以确定表示模型的不确定性的第一student-t分布的均值、比例和自由度的初始值。在一个实施方式中,student-t的均值与高斯的均值相同。在另一实施方式中,通过使高斯矩匹配到student-t来获得比例。在另一实施方式中,通过矩匹配和/或优化测量分布之间的差的成本函数来完成该拟合。
然后,该方法使用第一student-t分布的初始估计225a来确定230a表示状态不确定性的第二student-t分布的均值、比例和自由度235a的初始值。在一个实施方式中,通过使第一student-t的参数传播通过系统的运动模型来进行该确定。
然后,使用测量236a,该方法对系统的状态、第一student-t分布的参数和第二student-t分布的参数245a执行迭代更新240a,直至满足终止条件,其中,更新的参数245a也产生更新的第一student-t分布和第二student-t分布。
当满足终止条件时,该方法将表示状态不确定性的高斯分布拟合250a为第二student-t分布,以生成第二高斯分布的均值和方差255a。然后,该方法使用第二高斯分布的均值和方差255a来确定260a控制输入265a并根据控制输入265a来控制270a系统。
在一些实施方式中,第二student-t分布的初始值等于第一student-t分布的初始值。当没有理由或几乎没有理由相信状态的初始不确定性将从模型本身的初始不确定性改变时,选择这些初始值会是有利的。然而,在一个实施方式中,初始值不同。例如,一个实施方式将第二student-t分布的初始值确定为系统的模型和第一student-t分布的初始值的函数。例如,当已预先确定第一student-t分布的初始值,并且有理由相信自确定第一student分布的初始值以来系统的状态已改变时,这会是有价值的。在另一实施方式中,第二student-t分布的初始值等于第一student-t分布的初始值,但是第二student-t分布的最终值不同于第一student-t分布的最终值。通常是这种情况,除非系统的运动模型和系统的测量模型被建模为使得由两个模型引入的相应改变抵消。
图2b示出根据各种实施方式的210a的示例实现方式的流程图。首先,方法210a通过收集数据或者通过从存储器接收数据来获得210b系统的历史测量。然后,使用系统的模型219b,该方法确定220b历史测量的平均值以根据将状态与历史测量相关联的系统模型来生成均值的初始估计。然后,该方法使用历史测量的平均变化以及将状态与测量相关联的模型来确定230b方差的初始估计。
图2c示出根据一些实施方式的用于控制系统的设备210c的框图。该设备包括存储器220c,其存储系统的模型,该模型包括系统的受过程噪声影响的运动模型221c以及系统的受测量噪声影响的测量模型222c,使得过程噪声和测量噪声中的一个或组合形成具有未知或然性参数的系统模型的不确定性。系统模型的不确定性导致具有未知或然性参数的系统的状态不确定性223c。
设备210c还包括:传感器250c,其测量信号以生成指示系统的状态的一系列测量;处理器230c,其估计表示状态不确定性的高斯分布235c;以及控制器240c,其使用具有由高斯分布235c表示的状态不确定性的系统模型来确定对系统的控制输入,并根据控制输入来控制系统。控制器240c使用诸如模型预测控制的各种控制方法来控制系统,其由于不同的控制命令而使用系统模型(常常使用基础高斯噪声假设)进行系统的预测。另一可能的控制方法是lqg控制,其也依赖于基础高斯假设。将理解,实施方式不限于这些方法。
处理器230c基于表示模型的不确定性的第一student-t分布和表示系统的状态不确定性的第二student-t分布来确定高斯分布235c。例如,处理器使用系统的状态的测量、运动模型和测量模型中的至少一个或组合来估计第一和/或第二student-t分布。在一些实施方式中,该估计迭代地执行,直至满足终止条件。终止条件的示例包括已满足可用计算时限、已达到预定义的迭代次数以及两个连续更新之差低于预定义的阈值。在满足终止条件时,处理器将表示状态不确定性的高斯分布拟合为第二student-t分布。
这样,一些实施方式在高斯分布和student-t分布之间执行多个变换,以捕获过程的高斯性质和高斯性质的不确定性二者。这种变换允许在被设计为不考虑student-t分布的各种控制方法中考虑高斯分布的不确定性。
在一些实施方式中,自由度的初始值被选择为大于状态维度的维度的正有限整数值。在其它实施方式中,自由度大于状态维度和测量维度之和。在另一实施方式中,所确定的自由度的初始值用于确定第一student-t分布的均值和比例。例如,该实施方式将初始比例确定为第一高斯分布的初始方差除以初始自由度的仿射函数。
返回参照图1c,自由度的值表征student-t分布的尾部,因此表征对高斯扰动的参数中的不确定性的灵敏度。一些实施方式基于这样的理解:作用于系统模型的扰动是由于多个因素。例如,模型本身的参数和系统的输入二者可为不确定的。在这种设置中,扰动模型将多个扰动归并在一起。
因此,一个实施方式估计模型的不确定性级别,并作为模型中的不确定性级别的函数来选择自由度的初始值。
随着自由度增加,student-t分布接近高斯。一个实施方式基于这样的理解:避免这种合并会是有益的。因此,该实施方式限制student-t分布的参数,使得student-t和高斯彼此足够靠近,但不完全相同。例如,一个实施方式在满足迭代更新240a中的终止阈值之后确定有限的自由度。
高斯分布拟合到student-t分布(反之亦然)可按多个方式来完成。一个实施方式作为矩匹配和相似性优化之一或组合来确定第二高斯分布拟合250a为第二student-t分布。例如,一个实施方式通过将高斯的方差匹配到student-t的比例(通过将比例除以自由度的仿射函数)来确定拟合。在另一实施方式中,通过优化测量分布之间的差的成本函数来完成拟合。成本函数可按多个方式来选择,包括作为估计的student-t分布与高斯分布之间的差。
图3a示出根据本发明的实施方式的更新系统的状态、第一student-t分布的参数和第二student-t分布的参数的方法240a的一个迭代的流程图。该方法使用运动模型基于系统状态的先前估计、第一student-t分布的先前值和第二student-t分布的先前值来估计350a系统的状态、第一student-t分布的当前值和第二student-t分布的当前值。然后,该方法接收360a系统的测量。使用测量365a和测量模型345a,该方法基于估计的值355a来更新370a系统状态的当前估计、第一student-t分布的当前值和第二student-t分布的当前值。
有时,或然性参数随时间变化。例如,在使用惯性感测和/或gps的导航系统中,噪声统计常常具有时间相关性,其无法先验地确定。其它示例是由于近似非线性模型中的线性化误差引起的噪声统计变化,另一示例是环境相关传感器统计。
因此,一些实施方式基于这样的理解:更新240a、拟合第二高斯分布250a、确定控制输入260a和控制270a可能需要在不同的时间步执行。为此,一个实施方式针对不同的控制步迭代更新240a、拟合第二高斯分布250a、确定控制输入260a和控制270。这样做允许确定时变或然性参数。
在一些实施方式中,系统的状态根据系统状态的运动模型以动力学方式演进。如果仔细选择系统的运动模型和系统输入的模型,则系统状态的运动可被描述为独立于或然性参数的完全由车辆状态确定的一个部分以及一个不确定部分,其中不确定部分依赖于系统的噪声。在一些实施方式中,将未来时间步的状态与当前时间步的状态相关联的系统被写为xk+1=akxk+wk,其中,wk是过程噪声,xk是状态。测量模型的示例是yk=ckxk+ek,其中,ek是测量噪声。在一个实施方式中,替代地,模型被写为xk+1=axk+uk+wk,其中uk是系统的确定性输入,并且/或者对于测量模型是相似的。状态可描述诸如位置或速度的物理状态,或非物理状态。模型可从物理建模获得(例如,力和质量平衡),或者可从系统标识和黑箱模型获得。在另一实施方式中,原始系统模型是xk+1=f(xk,uk)+g(xk,uk)wk,其是非线性的,并且对于测量是相似的。然而,通过动力学的数学线性化,或者通过诸如统计线性化技术的其它技术,非线性模型可被变换为线性系统。
在一些实施方式中,状态和或然性参数通过概率方法来获得。根据概率密度函数(pdf),利用定义θk:={μk,∑k},其中参数是第一高斯分布的均值和方差,动力学系统可被描述为p(xk+1|xk,uk,θk)。一些实施方式依赖于这样的认识:确定系统的状态和或然性参数可通过给定测量以及运动模型和测量模型,确定总系统的pdf来完成。例如,在已知均值和未知方差的情况下,为了确定pdf,一些实施方式将pdf确定为状态的pdf和参数的pdf的乘积,如下:
其中st是student-t分布,iw是逆wishart分布。
一些实施方式基于这样的理解:各个时间步的动力学系统的状态可通过类似于kf的解析表达式来更新。
其它实施方式认识到,可通过测量与测量的状态估计之差来更新参数。一个实施方式以状态估计的不确定性对测量与测量的状态估计之差进行加权,以进一步考虑到状态估计的知识是不确定的。
例如,一个实施方式使用运动模型确定估计为
在一个实施方式中,使用测量来更新第二student-t分布通过估计的状态的加权差和测量与测量模型之间的差的组合来完成,其中通过第二student-t分布的比例和估计的第一student-t分布的比例的组合来确定加权。
在另一实施方式中,更新第一student-t分布通过将均值更新为估计的均值和估计的均值与更新的状态的均值的加权差的组合来完成。另选地或另外地,该更新基于测量模型作为测量与估计的测量之间的差来完成。一些实施方式通过测量与测量的状态估计之差与当前估计的比例的组合来更新比例。
其它实施方式认识到,可通过测量与测量的状态估计之差来更新参数。一个实施方式以状态估计的不确定性对测量与测量的状态估计之差进行加权,以进一步考虑到状态估计的知识是不确定的。
在更新与第二student-t分布有关的自由度时,一个实施方式将自由度更新为先前自由度与正值的组合,以增加自由度。在另一实施方式中,在估计自由度时,自由度以小于1的值缩放,以确保自由度不增长过快。这样做确保了student-t不会过快收敛于高斯。
在另一实施方式中,更新与第一student-t分布有关的自由度,一个实施方式将自由度更新为先前自由度与正值的组合,以增加自由度。在另一实施方式中,在估计自由度时,自由度以小于1的值缩放,以确保自由度不增长过快。这样做确保了student-t不会过快收敛于高斯。
在一个实施方式中,在迭代更新student-t分布时,并且在针对不同的控制步更新student-t分布时,自由度在各个迭代或各个控制步中被选择为第一student-t分布和第二student-t分布的自由度中的最小值。这样做确保了自由度保持为有限的,这确保了方法考虑或然性参数中的不确定性。
一个实施方式基于这样的理解:影响系统的运动模型的传感器和影响系统的测量模型的传感器常常受传感器测量的变化的知识的不确定性和时变偏移影响。另一实施方式基于传感器可由确定性部分和随机性部分的组合来建模,其中随机性部分由具有未知均值和方差的高斯分布来建模。各种实施方式认识到,高斯分布的均值和方差可用于对传感器测量的偏移和变化进行建模。因此,在一个实施方式中,通过确定高斯扰动的均值和方差来校准传感器。
一些实施方式认识到,可通过联合地考虑第一student-t分布的或然性参数和车辆的状态(即,第二student-t分布)来准确地估计或然性参数。在一个实施方式中,通过指派量的组合有多大可能说明测量向量的概率来估计这些量。
例如,图4a示出车辆具有初始状态410的场景。对于或然性参数的一个集合和系统的输入,车辆遵从运动411a并在430a结束,由于影响车辆运动的第一student-t的或然性参数中的不确定性而导致不确定性431a。模型的不确定性的方差导致直到特定区域420才可知道车辆的状态。然而,车辆430a的结束状态恰好位于区域420内,因此或然性参数和车辆的初始状态的该特定组合是良好组合的概率高。
图4b示出具有相同初始状态410的车辆,其具有影响运动模型的第一student-t分布的或然性参数的另一集合。对于相同的系统输入,车辆410现在遵从运动411b,导致车辆在状态430b结束,从而导致状态的第二student-t的不确定性431b。然而,车辆的该结束状态430b不位于影响测量模型的测量噪声的确定区域内。因此,初始状态和或然性参数的该特定组合是良好组合的概率低。
图4c示出根据本发明的各种实施方式所采用的一些原理确定的不同运动的示意图。估计车辆在具有道路边界440c的道路上处于当前状态410,其中根据本发明的其它实施方式在先前迭代期间确定了当前状态410的估计。线419c和429c是使用影响运动模型的或然性参数的两个不同集合确定的两个不同运动,从而导致车辆的两个可能的状态420c和430c。灰色区域411c指示影响测量模型的测量噪声的不确定性的估计,即,可能发生运动的可能区域,其根据在先前迭代期间确定的影响测量模型的估计的测量噪声来确定。仅运动419c在不确定性区域内。因此,由运动429c导致的状态420c以及与运动429c关联的或然性参数是良好组合的概率低。
如图4d所示,车辆的运动可在车辆状态上以pdf412d的形式建模,其中,pdf412d的初始条件409d已通过本发明的其它实施方式在先前迭代期间确定。在本发明的一些实施方式中,通过以下步骤计算运动;首先确定从初始状态到结束状态的运动分布,其中根据影响属于该特定运动的运动模型的第一student-t分布的或然性参数发起不同的运动;其次,确定根据第一student-t的分布的不同运动与测量模型中建模的传感器所测量的运动有多一致;第三,确定符合确定不同运动与感测系统所感测的真实运动有多一致的参数。为了例示,图4d示出过程噪声的两个不同的参数分别导致状态420c和430c,并且车辆运动的pdf412d均与相应运动一致的情况。然而,在确定不同运动与测量的pdf411c有多一致(其中pdf411c依赖于影响测量模型的测量噪声)之后,实现pdf431d,其不与状态420c一致。在一些实施方式中,pdf431d由先前迭代的估计与来自传感器的测量的组合来确定。在本发明的特定实施方式中,所得pdf431d形成该方法的另一迭代的基础。
一些实施方式基于这样的理解:使用传感器的测量并不总是影响系统的测量模型,而是另外地或另选地,传感器测量也影响系统的运动模型。例如,这种理解在汽车应用中可为重要的,其中来自驾驶者或车辆的控制器的转向输入是对车辆的运动模型的输入,从而影响车辆的速度。转向输入不完全已知,而是由附接到车辆的方向盘的噪声传感器测量。如果使用惯性测量(例如,加速度测量),则车辆的测量模型也包括来自驾驶者的转向输入。因此,车辆的测量模型中包含关于转向输入的信息。此外,由于传感器的构造或传感器中的未对准,传感器常常易于时变偏移和测量变化。另外,尽管可预先执行一些传感器校准(例如,当安装在车辆中时),但诸如加速度计的一些传感器可具有与先验确定不同的有效噪声级别。原因在于,传感器噪声取决于许多因素,例如温度、年龄以及传感器放置在车辆中的何处。例如,传感器放置得越高,来自悬架系统的扰动越影响传感器中的表观噪声。
图5a示出系统的传感器的测量510通常如何根据传感器的状态随时间变化的例示。如本文所使用的,传感器的状态包括指示系统运动的传感器读数的至少一个参数。传感器的状态参数的示例包括校准误差、偏移、温度相关性、白噪声强度、随机游走偏差、比例误差、增益误差和方差中的一个或组合。传感器状态的时间变化的模型通常是未知的,并且取决于内在因素和外在因素二者,并且定义传感器状态的各种参数可依赖于彼此。
例如,测量车辆的转速的陀螺仪传感器的传感器状态取决于多个因素,例如环境的温度、传感器组件本身的温度、传感器与车辆的对准、比例误差或传感器的电路中的周期性行为。如本文所使用的,车辆可以是任何类型的轮式车辆,例如乘用车、公共汽车或自行装置(rover)。如本文所使用的,传感器可以是测量与车辆的运动有关的实体的任何类型的感测装置。例如,传感器可以是加速度计、陀螺仪、全球定位系统接收器、测量车轮角度的传感器或轮编码器。通常,传感器读数510由恒定部分520、缓慢随时间变化的部分540以及关于车辆的运动而变化的部分530组成。
图5b示出车辆传感器的传感器偏移通常如何随传感器的放置变化的例示。图5b示出方向盘510b与车轮530b之间的相互作用的构造的示意图。转向柱配备有电动转向系统520b以帮助驾驶者操纵方向盘。另外在转向柱上还有测量车轮角度的传感器。根据传感器靠近511b方向盘还是靠近521b车轮放置,从而直接测量车轮角度,将获得不同的偏移,因为方向盘510b与车轮530b之间的机械构造具有动力学相关性并且涉及齿轮箱和其它机械零件。
传感器测量的方差也随时间变化,并且在很大程度上也依赖于传感器位于系统中的何处。图5c示出车辆传感器的传感器方差通常如何随传感器的放置变化的例示。例如,将加速度计510c相对于车辆的质心520c放置得越高导致加速度计也感测由于外部因素(例如,路面530c的不平或车辆的悬架系统540c)引起的变化。这导致传感器具有与内在传感器变化不同的有效方差,如果不考虑的话将产生估计误差。
因此,一个实施方式基于这样的理解:影响系统的运动模型的传感器和影响系统的测量模型的传感器常常受传感器测量的变化的知识的不确定性和时变偏移影响。另一实施方式基于传感器可由确定性部分和随机性部分的组合来建模,其中随机性部分由具有未知均值和方差的高斯分布来建模。各种实施方式认识到,高斯分布的均值和方差可用于对传感器测量的偏移和变化进行建模。因此,在一个实施方式中,通过确定高斯扰动的均值和方差来校准传感器。
传感器状态的时间演进是未知的,因此传感器状态的任何运动模型是未知的并且无法验证。
为此,一个实施方式认识到,由于传感器状态的运动的时间演进是未知的,但是未知部分通常随时间缓慢变化,所以传感器状态应该替代地被当作作用于运动模型以及另外地或另选地测量模型的随机扰动。即,代替明确地确定传感器的状态,相反确定传感器状态的分布,从而回避了传感器状态的运动模型的需要。
本发明的一个实施方式认识到,尽管确定传感器的状态是复杂的并且取决于难以建模的影响,但是可以表示传感器的偏移和传感器的方差的参数来概括传感器的行为。例如,返回图5a,恒定部分510和随时间缓慢变化的部分540可被视为传感器的偏移,而部分530取决于系统的运动,附加扰动来自于传感器的传感器噪声。
传感器偏移的知识可用于控制(例如,车辆的电子稳定性控制),其中使用横向加速度、航向角速度和车轮的转向角来控制车辆。在不知道偏移的情况下,车辆的控制器将基于错误的车辆模型来确定对车辆的控制输入。
传感器测量的方差的知识也可用于控制。例如,方差可用于确定传感器读数的可信度并关于传感器测量的变化的大小来调节控制输入。
为此,一些实施方式基于这样的认识:可将传感器中的偏移作为随机分布的统计均值而包括,其中,随机分布定义了描述传感器状态的随机扰动,并且可将传感器噪声作为传感器测量围绕随机分布的均值的变化而包括。其它实施方式基于这样的认识:将传感器建模为随机分布可用于系统的运动模型和系统状态的测量模型。在其它实施方式中,传感器状态的均值和方差被变换为student-t分布,以考虑或然性参数的不确定性。
图6a示出根据本发明的一个实施方式的通过联合估计系统的状态(例如,系统的速度和航向角速度)和系统的传感器状态来控制系统的方法的流程图。一个实施方式基于这样的认识:至少一个传感器的未知传感器状态可被视为作用于车辆的运动的(或确定性)模型的随机扰动。根据图4d,随机扰动的性质导致系统具有不同的可能运动,因此具有不同的可能状态。例如,运动模型的输入由车辆的噪声传感器测量。
为此,实施方式利用粒子611a来表示610a传感器状态和系统的状态。粒子包括系统的状态,其可以是测量的状态或在联合估计的先前迭代期间确定的状态。另外地或另选地,粒子包括系统状态的均值、自由度和比例以及定义传感器状态的可行空间的随机扰动的均值、偏移和比例、传感器的噪声。以概率方式(即,使用均值、自由度和比例)表示传感器状态允许将随机扰动视为对车辆运动的student-t。为此,实施方式使用传感器状态的可行空间的均值作为由传感器特性的参数(均值、自由度和比例)定义的运动模型609a的输入,并使用传感器状态的均值来联合估计。在其它实施方式中,当测量的传感器状态影响运动模型时,一个实施方式将传感器状态的可行空间的均值与估计的状态与测量的状态的加权差组合使用。
图6b示出例示了定义传感器状态的可行空间600b的概率分布函数640b的曲线图。函数640b的形状可预先确定。例如,如果传感器状态的分布为高斯的,则分布640b的形状为“高斯帽”形状。如果形状固定,则均值610b和方差630b定义分布640b以及可包含传感器状态的可行空间600b。在一些实施方式中,可行空间600b由均值、自由度和比例定义。
根据分布640b,值620b是正确传感器状态的概率高于650b的概率。这种表示允许更新660b传感器状态的均值和方差以生成定义更新的传感器状态可行空间的更新的分布645b。此实施方式基于这样的观察:传感器状态的均值和方差的更新影响后续迭代中使用的传感器状态的参数的值,因为这种参数形成更新的分布的基础。
为此,该方法更新620a粒子(包括传感器状态的均值、比例和自由度)以生成更新的粒子621a。例如,该实施方式利用使用粒子的可行空间的或然性参数估计的状态与测量的传感器状态619a的均值和比例之差来迭代地更新粒子的均值和比例,其中测量的传感器状态619a根据可包括传感器状态的测量模型608a从车辆状态的测量确定。
接下来,该方法将表示传感器状态的可行空间的高斯分布拟合630a为传感器状态的可行空间的student-t分布,以生成传感器状态的均值和方差631a。
在一个实现方式中,该方法使用以测量的状态为中心的测量模型的概率分布来确定车辆状态和传感器状态的概率分布。测量模型的概率分布可预先确定(例如,使用在先前时刻确定的传感器状态的值)。接下来,该方法根据粒子中的均值在车辆状态和传感器状态的概率分布上的放置来确定粒子表示传感器的真实状态的概率,并调节粒子以更好地表示传感器真实状态。这种概率和调节由函数629a用于确定输出631a。
图6c示出根据迭代地更新粒子的一个实施方式的更新粒子620a的方法的一个迭代的框图。该方法可使用车辆的处理器来实现。该方法确定610c车辆的运动模型中使用的可能参数的可行空间以生成包括或然性参数615c(即,均值、比例和自由度)的student-t分布。由于影响运动模型的传感器状态中的不确定性,车辆的运动模型605c包括车辆运动的不确定性。该方法使用车辆的运动模型605c和系统的输入617c来估计620c由于影响车辆运动的student-t分布而发生的可能状态625c。
接下来,该方法测量状态630c。例如,该方法测量取决于传感器状态的这种车辆状态。该方法将测量映射到将车辆状态和至少一个传感器的传感器状态相关联的测量模型,以生成测量、车辆状态和传感器状态之间的关系635c。该方法根据测量模型635c针对导致所测量的车辆状态的粒子将传感器的偏移确定640c为传感器状态的统计均值。该方法还将由传感器状态导致的所测量的传感器状态的比例确定640c为估计的状态与测量之间的差,另外地或另选地,确定为估计的状态与运动模型的确定性部分之间的差,其将导致该状态不存在未知传感器状态。使用650c确定645c的传感器状态的均值和比例将偏移更新为使用导致所测量的车辆状态的所测量的传感器状态的均值的粒子中的传感器状态的统计均值与在先前迭代期间确定的均值的组合。类似地,该方法使用所测量的传感器状态的比例与在先前迭代期间确定的比例的组合来更新650c粒子中的传感器状态的比例。
在一个实施方式中,测量的子集具有先验地或通过一些其它方法确定的已知方差和偏移(即,已知参数)。在这种情况下,通过使用具有已知参数的传感器来估计车辆状态的部分,可使用具有已知方差和偏移的测量来改进具有未知参数的传感器的传感器特性的均值和比例的估计。在一个实施方式中,具有已知参数的传感器的均值和方差在用于确定传感器状态之前根据其它实施方式被变换为均值、自由度和比例。
图7a示出控制系统699的一般框图。控制系统699的不同组件可使用在操作上连接到系统的存储器和/或各种类型的传感器的一个或多个处理器来实现。控制系统699可在系统700内部,并且控制系统699的不同组件的实现方式通常取决于系统的类型。
控制系统699可包括感测系统730,其测量关于系统的至少一些部分的运动的信息。感测系统730还可从外部源接收感测信息729。
控制系统199还包括传感器状态估计器740以用于确定传感器(例如,730中的传感器)的状态的参数。在本发明的一些实施方式中,传感器状态估计器根据在先前迭代期间确定的系统的状态和传感器状态的或然性参数迭代地确定系统的状态和表示传感器状态的或然性参数。
传感器状态估计器740使用来自感测系统的信息731。传感器状态估计器740还可从系统控制单元760接收关于系统运动的信息761。该信息可包括系统的状态,并且从直接或远程连接到机器的硬件或软件接收。
例如,传感器状态估计器可输出传感器状态741,其包括测量的噪声的偏移值、偏移的确定性级别和方差或其组合。控制系统699还包括使用传感器状态信息741的系统控制器760。例如,在一个实施方式中,如果系统是道路车辆,则在利用车辆的动力学模型(取决于传感器的偏移状态)的高级驾驶者辅助系统(adas)中使用偏移。在这种情况下,车辆控制器760可包括允许自主驾驶特征的独立组件或车辆控制器的组合。描述传感器状态的偏移和方差可用作车辆的估计器790(例如,状态估计器)的输入。
图7b示出根据本发明的一个实施方式的传感器状态估计器740的一般结构。传感器状态估计器740包括至少一个处理器770以用于执行传感器状态估计器740的模块。处理器770连接771到存储状态和参数的统计781以及系统信息782(例如,运动模型和测量模式)的存储器780,其中,运动模型包括运动的确定性分量和运动的或然性分量的组合,其中,运动的确定性分量独立于传感器状态并且作为时间的函数来定义系统的运动,其中,运动的或然性分量包括传感器状态并且定义系统运动上的扰动,其中,车辆的测量模型包括独立于传感器状态的测量模型的确定性分量和包括传感器状态的测量模型的或然性分量的组合。存储器780还存储783估计器的内部信息,包括但不限于传感器状态的值、计算的系统状态的值以及导致各个系统状态的运动。在一些实施方式中,基于从系统761和感测731接收的信息来更新771关于系统的信息。
本发明的上述实施方式可按照众多方式中的任一种来实现。例如,实施方式可使用硬件、软件或其组合来实现。当以软件实现时,软件代码可在任何合适的处理器或处理器集合上执行(无论设置在单个计算机中还是分布于多个计算机)。这些处理器可被实现为集成电路,在集成电路组件中具有一个或更多个处理器。但是,处理器可使用任何合适格式的电路来实现。
另外,本文概述的各种方法或过程可被编码为软件,该软件可在采用各种操作系统或平台中的任一种的一个或更多个处理器上执行。另外,这种软件可使用许多合适的编程语言和/或编程或脚本工具中的任一种来编写,并且也可被编译为在框架或虚拟机上执行的可执行机器语言代码或中间代码。通常,在各种实施方式中,程序模块的功能可根据需要被组合或分布。
另外,本发明的实施方式可被具体实现为一种方法,已提供该方法的示例。作为该方法的一部分执行的动作可按照任何合适的方式排序。因此,可构造以与所示不同的次序执行动作的实施方式,其可包括同时执行一些动作,尽管在例示性实施方式中作为顺序动作示出。
- 该技术已申请专利。仅供学习研究,如用于商业用途,请联系技术所有人。
- 技术研发人员:K·贝恩拓普;S·迪卡拉诺
- 技术所有人:三菱电机株式会社
- 我是此专利的发明人
- 该领域下的技术专家
- 如您需求助技术专家,请点此查看客服电话进行咨询。
- 1、唐老师:1.高效节能装备 2.流动稳定性 3.汽车流场分析和淀粉糖工艺技术。
- 2、孙老师:1.振动信号时频分析理论与测试系统设计 2.汽车检测系统设计 3.汽车电子控制系统设计
- 3、王老师:电子信息处理、先进检测方法和智能化仪表
- 4、周老师:1.智能电网 2.新能源利用 3.泛在电力物联网
- 5、赵老师:检测与控制技术、机器人技术、机电一体化技术
- 如您是高校老师,可以点此联系我们加入专家库。
- 还没有人留言评论。精彩留言会获得点赞!