采用单值中智余弦相似度量和遗传算法的PID参数整定方法与流程

本发明涉及工业自动化控制技术领域，特别涉及采用单值中智余弦相似度量和遗传算法的pid参数整定方法。

背景技术：

pid控制是过程控制中广泛应用的一种控制。按偏差的比例(proportion)、积分(integral)、微分(derivative)控制,简称pid控制。由于pid控制器有着结构简单、稳定性好、工作可靠、调整方便等优点，已成为了工业控制的主要控制技术之一。在pid控制器投入应用之前都需要进行pid参数整定以获得pid整定参数，所述pid控制器利用所述pid整定参数控制所述被控对象运行。

现有技术中进行pid参数整定的方法通常是利用继电器法获得被控对象的数学模型，然后利用ziegler-nichols或极点配置等方法来整定pid参数，获得所述pid整定参数，现有的pid参数整定方法操作不便，并且其整定效果不理想。

技术实现要素：

发明的目的在于提供采用单值中智余弦相似度量和遗传算法的pid参数整定方法，通过设计实例对所提出的整定方法进行了设计验证，仿真结果表明了所提出的pid参数整定方法的有效性和方便性，以解决上述背景技术中提出的问题。

为实现上述目的，本发明提供如下技术方案：

采用单值中智余弦相似度量和遗传算法的pid参数整定方法，包括单值中智余弦相似度量和遗传算法两个部分，其中单值中智余弦相似度量包括如下步骤：

s1：建立单值中智隶属函数

选定三角形和梯形隶属函数用于中智化过程，选定六种瞬态特性的隶属函数作为特性集c＝{c1，c2，c3，c4，c5，c6}，可以根据实际应用对象确定单值中智集中的ti，ii和fi(i＝1,2，...，6)隶属函数的类型及其范围值，通过隶属函数可以得到单值中智集s＝{<c1,t1,i1,f1>,<c2,t2,i2,f2>,<c3,t3,i3,f3>,<c4,t4,i4,f4>,<c5,t5,i5,f5>,<c6,t6,i6,f6>}，那么理想的单值中智集s^*＝{<c1,1,0,0>,<c2,1,0,0>,<c3,1,0,0>,<c4,1,0,0>,<c5,1,0,0>,<c6,1,0,0>}；

s2：单值中智余弦相似度量

s和s^*之间的余弦相似度量可以定义为：

遗传算法的步骤包括：随机生成n个kp，ki和kd值的解集作为初始种群，通过选择、交叉、变异寻找最优kp，ki和kd值，以达到适值函数的最小值(minf)。

进一步地，还包括pid控制器，pid控制器输出如下：

进一步地，s1中包含六种瞬态特性隶属函数。

进一步地，为了获得pid控制系统的最优控制性能，作为最小函数值的优化问题，可以建立如下的适值函数：minf＝1-cs(s,s^*)，然后，在pid控制器中使用三个参数kp，ki，kd的实值编码。

进一步地，为了显示所提pid参数整定方法的有效性,给出以下开环传递函数：

进一步地，遗传算法的搜索参数范围被定为1≤kp≤30,0≤ki≤30,0≤kd≤30，种群大小n＝20，交叉概率pc＝0.9，变异概率pm＝0.1，运算终止条件为f＝0.017。

与现有技术相比，本发明的有益效果是：本发明提出的采用单值中智余弦相似度量和遗传算法的pid参数整定方法，在pid参数整定过程中，控制系统的阶跃响应特性值(上升时间，调整时间，超调率，下调率，峰值时间和稳态误差)通过中智隶属函数被转换成单值中智集。通过遗传算法来确定pid控制器中的三个最优参数值，其优化目标是实际输出的单值中智集和先前确定的理想单值中智集之间的相似性度量达到最大值。最后，通过设计实例对所提出的整定方法进行了设计验证，仿真结果表明了所提出的pid参数整定方法的有效性和方便性。

附图说明

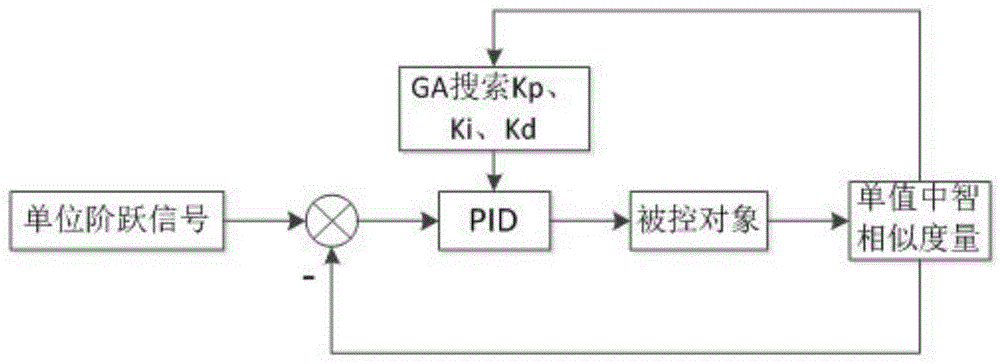
图1为本发明控制系统的pid参数整定方法原理图；

图2为本发明的六种瞬态特性的隶属函数图；

图3为本发明的遗传算法流程图；

图4为本发明的基于余弦相似度量和ga的阶跃响应图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

采用单值中智余弦相似度量和遗传算法的pid参数整定方法，包括单值中智余弦相似度量和遗传算法两个部分，其原理如图1，还包括pid控制器，pid控制器输出如下：

其中单值中智余弦相似度量包括如下步骤：

(1)建立单值中智隶属函数

选定三角形和梯形隶属函数用于中智化过程，六种瞬态特性隶属函数如图2所示，图中，(1)c1：上升时间(s)，(2)c2：调整时间(s)，c3：超调率(％)，(4)c4：下调率(％)，(5)c5：峰值时间(s)，以及(6)c6：稳态误差。选定六种瞬态特性的隶属函数作为特性集c＝{c1，c2，c3，c4，c5，c6}，可以根据实际应用对象确定单值中智集中的ti，ii和fi(i＝1,2，...，6)隶属函数的类型及其范围值，通过图2中的隶属函数可以得到单值中智集s＝{<c1,t1,i1,f1>,<c2,t2,i2,f2>,<c3,t3,i3,f3>,<c4,t4,i4,f4>,<c5,t5,i5,f5>,<c6,t6,i6,f6>}，那么理想的单值中智集s^*＝{<c1,1,0,0>,<c2,1,0,0>,<c3,1,0,0>,<c4,1,0,0>,<c5,1,0,0>,<c6,1,0,0>}；

(2)单值中智余弦相似度量

s和s^*之间的余弦相似度量可以定义为：

(3)遗传算法(ga)

遗传算法可以用来解决广泛的优化问题，为了获得pid控制系统的最优控制性能，作为最小函数值的优化问题，可以建立如下的适值函数：

minf＝1-cs(s,s^*)

然后，在pid控制器中使用三个参数kp，ki，kd的实值编码。一般而言，ga包含的典型算法如图3所示。

ga算法过程如下：随机生成n个kp，ki和kd值的解集作为初始种群，通过选择、交叉、变异寻找最优kp，ki和kd值，以达到适值函数的最小值(minf)。

(4)pid参数整定实例

为了显示所提pid参数整定方法的有效性,给出以下开环传递函数：

作为pid参数整定的设计实例。

在pid控制器设计中，使用基于实数值编码的ga算法来搜索kp，ki和kd三个pid参数值，ga的搜索参数范围被定为1≤kp≤30,0≤ki≤30,0≤kd≤30，种群大小n＝20，交叉概率pc＝0.9，变异概率pm＝0.1，运算终止条件为f＝0.017。图4给出了在最终kp，ki和kd值的阶跃响应曲线。最大度量值和pid参数的相应值如表1所示；对应于得到的kp，ki，kd值，g1(s)的阶跃响应特性如表2所示。

表1最大余弦相似度量值时的pid参数整定值

表2基于余弦相似度量和ga的g1(s)阶跃响应特性

在表1中，对应于kp＝1.9122，ki＝1.0635，kd＝0.9517，ga运算中第42代的最大余弦相似性度量值为0.9833，而表2和图4分别显示了相应的阶跃响应特性值和曲线。由于余弦相似性度量值非常接近于1，因此这些结果说明了所提pid参数整定方法的有效性和合理性。

综上所述，本发明提出的采用单值中智余弦相似度量和遗传算法的pid参数整定方法，在pid参数整定过程中，控制系统的阶跃响应特性值(上升时间，调整时间，超调率，下调率，峰值时间和稳态误差)通过中智隶属函数被转换成单值中智集。通过遗传算法来确定pid控制器中的三个最优参数值，其优化目标是实际输出的单值中智集和先前确定的理想单值中智集之间的相似性度量达到最大值。最后，通过设计实例对所提出的整定方法进行了设计验证，仿真结果表明了所提出的pid参数整定方法的有效性和方便性。

值得说明的是，本发明中：ti代表“真”，ii代表“不确定”和fi代表“假”。

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明披露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。