MIMO异因子全格式无模型控制方法与流程

本发明属于自动化控制领域，尤其是涉及一种mimo异因子全格式无模型控制方法。

背景技术：

炼油、石化、化工、制药、食品、造纸、水处理、火电、冶金、水泥、橡胶、机械、电气等行业的大多数被控对象，包括反应器、精馏塔、机器、设备、装置、生产线、车间、工厂，本质上都是mimo(multipleinputandmultipleoutput，多输入多输出)系统。实现对mimo系统的高精度、高稳定、高适用性控制，对工业的节能降耗、提质增效具有重要意义。然而，mimo系统的控制难题，尤其是强非线性mimo系统的控制难题，一直以来都是自动化控制领域所面临的重大挑战。

mimo系统的现有控制方法中包括mimo全格式无模型控制方法。mimo全格式无模型控制方法是一种新型的数据驱动控制方法，不依赖被控对象的任何数学模型信息，仅依赖于mimo被控对象实时测量的输入输出数据进行控制器的分析和设计，并且实现简明、计算负担小及鲁棒性强，具有良好的应用前景。mimo全格式无模型控制方法的理论基础，由侯忠生与金尚泰在其合著的《无模型自适应控制—理论与应用》(科学出版社，2013年，第116页)中提出，其控制算法如下：

其中，u(k)为k时刻控制输入向量，u(k)＝[u1(k),…,um(k)]^t，m为控制输入总个数(m为大于1的正整数)，δu(k)＝u(k)-u(k-1)；e(k)为k时刻误差向量，e(k)＝[e1(k),…,en(k)]^t，n为输出总个数(n为正整数)；δy(k)＝y(k)-y(k-1)，y(k)为k时刻输出实际值向量，y(k)＝[y1(k),…,yn(k)]^t；φ(k)为k时刻mimo系统伪分块雅克比矩阵估计值，φp(k)为φ(k)的第p块(p为正整数，1≤p≤ly+lu)，||φly+1(k)||为矩阵φly+1(k)的2范数；λ为惩罚因子；ρ1,…,ρly+lu为步长因子；ly为控制输出线性化长度常数，ly为正整数；lu为控制输入线性化长度常数，lu为正整数。

上述现有的mimo全格式无模型控制方法，采用了同因子结构，也就是说：在k时刻，针对控制输入向量u(k)中的不同控制输入u1(k),…,um(k)，只能采用相同数值的惩罚因子λ与相同数值的步长因子ρ1，…，相同数值的步长因子ρly+lu。当现有的mimo同因子全格式无模型控制方法应用于强非线性mimo系统等复杂对象时，由于控制通道特性各异，往往难以实现理想的控制效果，制约了mimo全格式无模型控制方法的推广应用。

为此，为了打破现有的mimo同因子全格式无模型控制方法的应用瓶颈，本发明提出了一种mimo异因子全格式无模型控制方法。

技术实现要素：

为了解决背景技术中存在的问题，本发明的目的在于，提供一种mimo异因子全格式无模型控制方法，其特征在于：

当被控对象为mimo(multipleinputandmultipleoutput，多输入多输出)系统时，所述mimo异因子全格式无模型控制方法计算k时刻第i个控制输入ui(k)的数学公式如下：

如果控制输入线性化长度常数lu＞1，则：

如果控制输入线性化长度常数lu＝1，则：

其中，k为正整数；m为所述mimo系统控制输入总个数，m为大于1的正整数；n为所述mimo系统输出总个数，n为正整数；i表示所述mimo系统控制输入总个数中的第i个，i为正整数，1≤i≤m；j表示所述mimo系统输出总个数中的第j个，j为正整数，1≤j≤n；ui(k)为k时刻第i个控制输入；δuiu(k)＝uiu(k)-uiu(k-1)，iu为正整数；ej(k)为k时刻第j个误差，即k时刻误差向量e(k)＝[e1(k),…,en(k)]^t的第j个元素；δyjy(k)＝yjy(k)-yjy(k-1)，yjy(k)为k时刻第jy个输出实际值，jy为正整数；φ(k)为k时刻mimo系统伪分块雅克比矩阵估计值，φp(k)为φ(k)的第p块，φj,i,p(k)为矩阵φp(k)的第j行第i列元素，||φly+1(k)||为矩阵φly+1(k)的2范数；p为正整数，1≤p≤ly+lu；λi为第i个控制输入的惩罚因子；ρi,p为第i个控制输入的第p个步长因子；ly为控制输出线性化长度常数，ly为正整数；lu为控制输入线性化长度常数，lu为正整数；

针对mimo系统，所述mimo异因子全格式无模型控制方法将i的取值遍历正整数区间[1,m]内的所有值，即可计算得到k时刻控制输入向量u(k)＝[u1(k),…,um(k)]^t；

所述mimo异因子全格式无模型控制方法具有异因子特征；所述异因子特征是指针对正整数区间[1,m]内任意两个互不相等的正整数i与x，在采用所述控制方法对mimo系统进行控制期间，如下(ly+lu+1)个不等式中至少有一个不等式成立：

λi≠λx；ρi,1≠ρx,1；…；ρi,ly+lu≠ρx,ly+lu

在采用上述技术方案的同时，本发明还可以采用或者组合采用以下进一步的技术方案：

所述k时刻第j个误差ej(k)采用第j个误差计算函数计算得到；所述第j个误差计算函数的自变量包含第j个输出期望值与第j个输出实际值。

所述第j个误差计算函数采用其中为k时刻第j个输出期望值，yj(k)为k时刻第j个输出实际值；或者采用其中为k+1时刻第j个输出期望值；或者采用或者采用

所述被控对象包含反应器、精馏塔、机器、设备、装置、生产线、车间、工厂。

运行本发明所述控制方法的硬件平台包含工业控制计算机、单片机控制器、微处理器控制器、现场可编程门阵列控制器、数字信号处理控制器、嵌入式系统控制器、可编程逻辑控制器、集散控制系统、现场总线控制系统、工业物联网控制系统、工业互联网控制系统的任意之一或任意种组合。

本发明提供的mimo异因子全格式无模型控制方法，针对控制输入向量中的不同控制输入可采用不同数值的惩罚因子或不同数值的步长因子，能够解决强非线性mimo系统等复杂对象中存在的各个控制通道特性各异的控制难题。因此，与现有的mimo同因子全格式无模型控制方法相比，本发明提供的mimo异因子全格式无模型控制方法具有更高的控制精度、更好的稳定性与更广的适用性。

附图说明

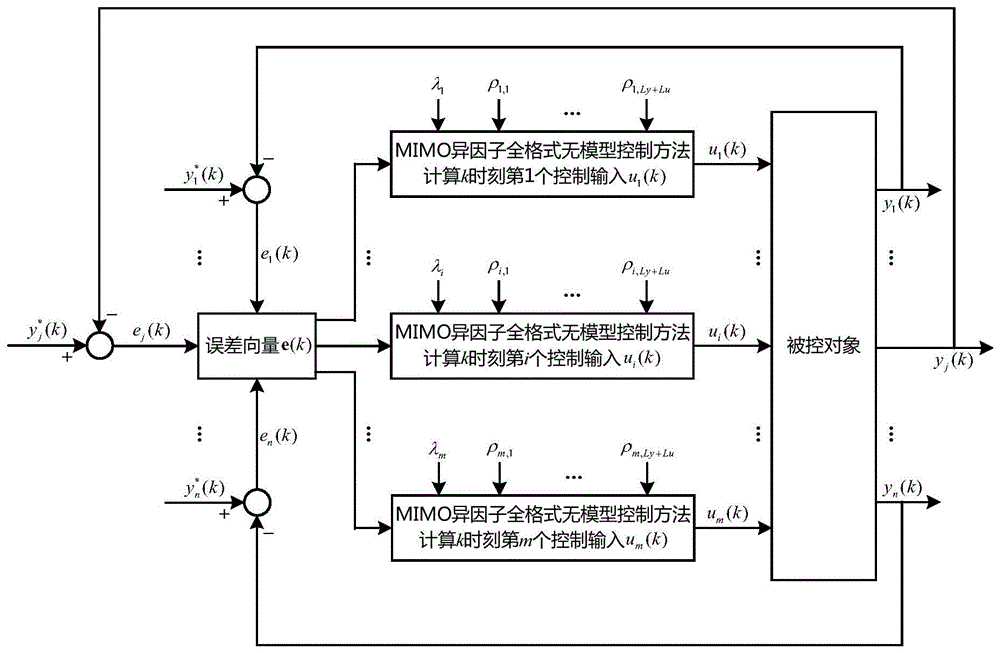
图1为本发明的原理框图；

图2为两输入两输出mimo系统采用本发明的mimo异因子全格式无模型控制方法时第1个输出的控制效果图；

图3为两输入两输出mimo系统采用本发明的mimo异因子全格式无模型控制方法时第2个输出的控制效果图；

图4为两输入两输出mimo系统采用本发明的mimo异因子全格式无模型控制方法时的控制输入曲线；

图5为两输入两输出mimo系统采用现有的mimo同因子全格式无模型控制方法时第1个输出的控制效果图；

图6为两输入两输出mimo系统采用现有的mimo同因子全格式无模型控制方法时第2个输出的控制效果图；

图7为两输入两输出mimo系统采用现有的mimo同因子全格式无模型控制方法时的控制输入曲线。

具体实施方式

下面结合附图和具体实施例对本发明进一步说明。

图1给出了本发明的原理框图。针对具有m个控制输入(m为大于1的正整数)与n个输出(n为正整数)的mimo系统，采用mimo异因子全格式无模型控制方法进行控制；确定mimo异因子全格式无模型控制方法的控制输出线性化长度常数ly，ly为正整数；确定mimo异因子全格式无模型控制方法的控制输入线性化长度常数lu，lu为正整数；针对第i个控制输入ui(k)(i＝1,…,m)，确定mimo异因子全格式无模型控制方法用于计算ui(k)的数学公式中所有参数包含惩罚因子λi、步长因子ρi,1,…,ρi,ly+lu的数值；将当前时刻记为k时刻；将第j个输出期望值与第j个输出实际值yj(k)之差作为k时刻第j个误差ej(k)；将j的取值遍历正整数区间[1,n]内的所有值，得到误差向量e(k)＝[e1(k),…,en(k)]^t；基于k时刻误差向量e(k)＝[e1(k),…,en(k)]^t与惩罚因子λi、步长因子ρi,1,…,ρi,ly+lu的数值，采用mimo异因子全格式无模型控制方法计算k时刻第i个控制输入ui(k)；针对mimo系统，mimo异因子全格式无模型控制方法将i的取值遍历正整数区间[1,m]内的所有值，即可计算得到k时刻控制输入向量u(k)＝[u1(k),…,um(k)]^t；控制输入向量u(k)作用于被控对象后，得到被控对象在后一时刻的n个输出实际值，然后进行后一时刻的mimo异因子全格式无模型控制。

以下是本发明的具体实施例。

被控对象采用的两输入两输出mimo系统，具有非最小相位非线性系统的复杂特征，属于特别难以控制的mimo系统：

系统输出期望值y^*(k)如下：

在具体实施例中，m＝n＝2。

控制输出线性化长度常数ly的数值通常根据被控对象的复杂程度和实际的控制效果进行设定，一般在1到5之间，过大会导致计算量大，所以一般常取1或3，在本具体实施例中ly取为1；控制输入线性化长度常数lu的数值也通常根据被控对象的复杂程度和实际的控制效果进行设定，一般在1到10之间，过小会影响控制效果，过大会导致计算量大，所以一般常取3或5，在本具体实施例中lu取为3。

针对上述具体实施例，开展两组试验进行对比验证。第一组试验采用本方明的控制方法，第二组试验采用现有的控制方法。为了更清楚地比较两组试验的控制性能，采用均方根误差(rootmeansquareerror,rmse)作为控制性能评价指标：

其中，为k时刻第j个输出期望值，yj(k)为k时刻第j个输出实际值。rmse(ej)的值越小，表明第j个输出实际值yj(k)与第j个输出期望值的误差总体而言更小，控制性能更好。

运行本发明控制方法的硬件平台采用工业控制计算机。

第一组试验时：采用本发明的mimo异因子全格式无模型控制方法，设定第1个控制输入的惩罚因子λ1＝1.01，第一个步长因子ρ1,1＝0.49，第二个步长因子ρ1,2＝0.49，第三个步长因子ρ1,3＝0.51，第四个步长因子ρ1,4＝0.50；设定第2个控制输入的惩罚因子λ2＝1.08，第一个步长因子ρ2,1＝0.50，第二个步长因子ρ2,2＝0.51，第三个步长因子ρ2,3＝0.52，第四个步长因子ρ2,4＝0.50；然后，对上述两输入两输出mimo系统进行控制，图2为第1个输出的控制效果图，图3为第2个输出的控制效果图，图4为控制输入曲线；从控制性能评价指标进行考察，图2中第1个输出的rmse(e1)为0.5426，图3中第2个输出的rmse(e2)为0.9951。

第二组试验时：直接采用现有的mimo同因子全格式无模型控制方法，设定惩罚因子λ＝1.00，设定步长因子ρ1＝ρ2＝ρ3＝ρ4＝0.50，对上述两输入两输出mimo系统进行控制，图5为第1个输出的控制效果图，图6为第2个输出的控制效果图，图7为控制输入曲线；从控制性能评价指标进行考察，图5中第1个输出的rmse(e1)为0.5433，图6中第2个输出的rmse(e2)为1.0194。

两组试验控制性能评价指标的比较结果列于表1，采用本发明控制方法的第一组试验的结果优于采用现有的mimo同因子全格式无模型控制方法的第二组试验，其中通过对比图3与图6可以发现改进效果显著，充分表明本发明提供的mimo异因子全格式无模型控制方法具有更高的控制精度、更好的稳定性与更广的适用性。

更进一步地，还应该特别指出以下三点：

(1)炼油、石化、化工、制药、食品、造纸、水处理、火电、冶金、水泥、橡胶、机械、电气等行业的大多数被控对象，包括反应器、精馏塔、机器、设备、装置、生产线、车间、工厂，本质上都是mimo系统，其中一些mimo系统具有非最小相位非线性系统的复杂特征，属于特别难以控制的mimo系统；举例来说，比如炼油、石化、化工、制药等行业常用的连续搅拌反应器cstr就是常见的两输入两输出mimo系统，其两个控制输入分别是进料流量与冷却水流量，其两个输出分别是产物浓度与反应温度；当化学反应具有强放热效应时，连续搅拌反应器cstr的mimo系统就具有非最小相位非线性系统的复杂特征，是典型的难控对象。在上述具体实施例中，被控对象采用的两输入两输出mimo系统，也具有非最小相位非线性系统的复杂特征，属于特别难以控制的mimo系统；本发明对该被控对象能够实现高精度、高稳定、高适用性的控制，说明本发明的控制方法也能够对反应器、精馏塔、机器、设备、装置、生产线、车间、工厂等复杂mimo系统实现高精度、高稳定、高适用性的控制。

表1控制性能比较

(2)在上述具体实施例中，运行本发明控制方法的硬件平台为工业控制计算机；在实际应用时，还可以根据具体情况，选择单片机控制器、微处理器控制器、现场可编程门阵列控制器、数字信号处理控制器、嵌入式系统控制器、可编程逻辑控制器、集散控制系统、现场总线控制系统、工业物联网控制系统、工业互联网控制系统的任意之一或任意种组合作为运行本发明控制方法的硬件平台。

(3)在上述具体实施例中，将第j个输出期望值与第j个输出实际值yj(k)之差作为k时刻第j个误差ej(k)，也就是仅为所述第j个误差计算函数中的一种方法；也可以将k+1时刻第j个输出期望值与k时刻第j个输出yj(k)之差作为第j个误差ej(k)，也就是所述第j个误差计算函数还可以采用自变量包含第j个输出期望值与第j个输出实际值的其他计算方法，举例来说，对上述具体实施例的被控对象而言，采用上述不同的误差计算函数，都能够实现良好的控制效果。

上述具体实施方式用来解释说明本发明，仅为本发明的优选实施例，而不是对本发明进行限制，在本发明的精神和权利要求的保护范围内，对本发明作出的任何修改、等同替换、改进等，都落入本发明的保护范围。