一种基于混沌多项式和序列凸优化的飞行器轨迹优化方法与流程

本发明涉及飞行器轨迹优化设计技术领域，具体涉及一种基于混沌多项式扩展(pce)理论和序列凸优化方法的飞行器轨迹稳健优化方法。

背景技术：

轨迹优化是飞行器优化设计中一个重要的组成部分，目的是为了确定飞行过程中同时满足动力学约束、边界条件、过程约束等约束的最优控制量，实质是一种优化控制问题，近年来得到了广泛的关注。但多数研究一般只关注标称轨迹性能，而不考虑轨迹的鲁棒性。在实际弹道飞行过程中，不确定性是不可避免的。例如，初始状态及系统参数的偏差可能会导致飞行器再入过程中实际轨迹偏离标称轨迹。由于传统的轨迹优化结果容易出现路径约束及边界约束满足裕度过低的情况，而实际扰动因素的作用下往往会违反约束。因此，通过采用轨迹稳健优化方法，设计一条在保证优良性能的同时对不确定性因素不敏感的飞行轨迹显得尤为重要。

目前飞行器轨迹稳健优化相关的研究有如下缺点：

(1)高维非线性规划(nlp)问题难以得到全局最优解。直接打靶法、伪谱法等直接优化算法在轨迹优化问题中得到广泛应用，它通过离散控制变量或同时离散控制变量与状态变量，把最优控制问题转化为非线性规划问题进行求解。但是，该类算法的收敛性依赖于初值的选择，易陷于局部最优，难以得到全局最优解。

(2)非线性规划问题求解属于np-hard问题。由于干涉式混沌多项式扩展方法需要将随机动力学微分方程扩展到高维确定性微分方程，维数可能扩张为原微分方程的几倍甚至几十倍，这将极大地增加了nlp求解的时间及难度。

技术实现要素：

有鉴于此，本发明提供了一种基于混沌多项式和序列凸优化的飞行器轨迹优化方法，能够解决飞行器轨迹稳健优化问题中存在不确定性分析与优化循环嵌套导致求解困难的问题。

本发明的基于混沌多项式和序列凸优化的飞行器轨迹优化方法，包括如下步骤：

步骤一，构建飞行器轨迹稳健优化数学模型；

步骤二，根据广义混沌多项式理论将步骤一获得的数学模型中的随机微分方程扩展为由混沌多项式系数构成的高维常微分方程；

步骤三，利用步骤二获得的混沌多项式系数，将步骤一的迹稳健优化数学模型转化为等效的确定性最优控制问题；结合步骤二获得的高维常微分方程，获得确定性的稳健优化模型；

步骤四，对确定性的稳健优化模型中的动力学微分方程在参考轨迹处进行一阶泰勒展开，实现凸化；

步骤五，根据广义混沌多项式理论，利用步骤四凸化后的方程，计算获得飞行器轨迹稳健优化数学模型中状态、约束、性能函数的均值及标准差；

步骤六，将步骤五获得的状态、约束、性能函数的均值及标准差代入步骤三的确定性的稳健优化模型，并对模型中的非凸约束、性能函数进行凸化处理，转化为二阶锥规划问题；

步骤七，对步骤六获得的二阶锥规划问题进行离散后通过内点法求解，得到最优控制变量，完成飞行器轨迹优化。

进一步的，所述步骤一中，对构建的轨迹稳健优化数学模型中的积分项以及非凸约束进行凸化处理后，转入步骤二。

进一步的，所述步骤六中，对状态变量的边界约束采用cholesky分解法转化为二阶锥约束；对其余的非凸约束以及性能函数采用在参考轨迹处进行一阶泰特展开，转化为二阶锥约束。

有益效果：

根据混沌多项式理论，不确定性传播的分析计算需要将低维的随机微分动力学方程组扩展为由pce系数构成的高维确定性常微分动力学方程组。具体维数关系是每一个随机微分动力学方程需要扩展成为个确定性常微分动力学方程组，这将极大地增加轨迹优化(最优控制问题)的计算量。通常，求解此类优化问题一般采用直接法，即离散其控制变量(如直接打靶法)或同时离散控制变量和状态变量(如伪谱法)等，将其转化为非线性规划(nlp)问题进行求解。但是，非线性规划问题属于np-hard问题，随着维数的增加，求解难度也急剧增大。凸规划是一种特殊的非线性规划，它的局部最优解就是全局最优解，而且求解效率高，属于多项式时间复杂度算法。因此，将最优控制问题转化为凸优化问题，能极大的提高问题求解效率。

附图说明

图1为本发明流程图。

图2为航天器着陆示意图。

图3为高斯伪谱法与序列凸优化方法在求解确定性轨迹优化问题时各参量曲线对比；(a)控制变量tc曲线；(b)状态变量r曲线；(c)状态变量v曲线；(d)最优轨迹曲线。

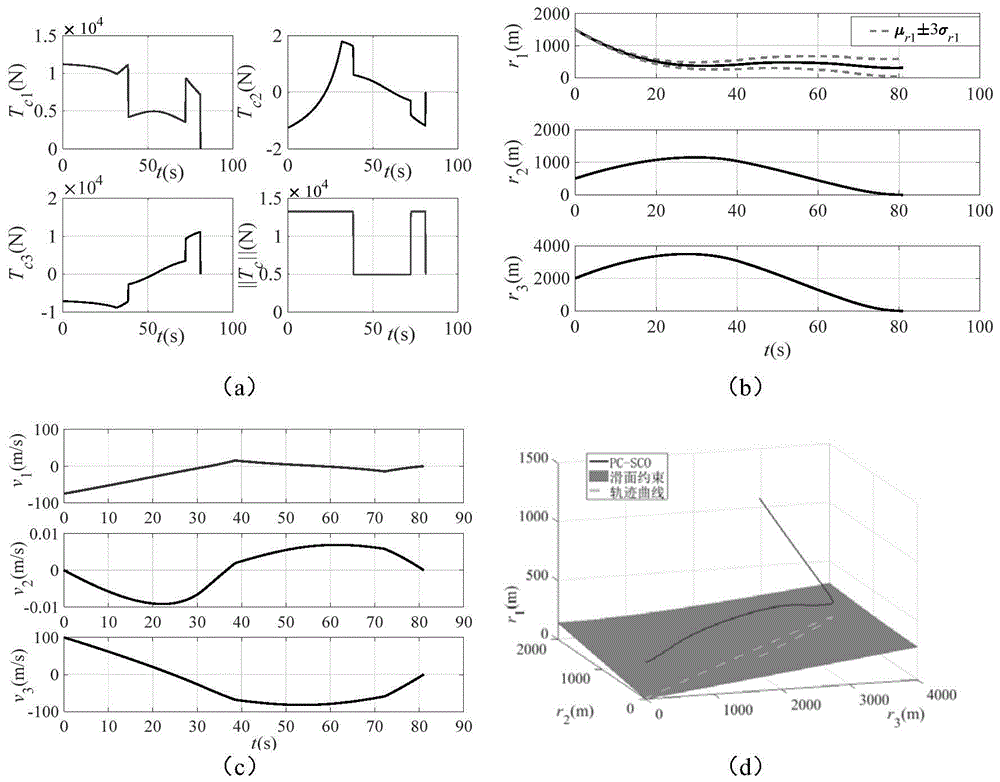
图4为本发明方法在求解稳健轨迹优化问题时各参量曲线；(a)控制变量tc曲线；(b)状态变量r曲线；(c)状态变量v曲线；(d)最优轨迹曲线。

图5为稳健优化(ro)结果及确定性优化(do)结果做蒙特卡罗仿真(mcs)对比：(a)状态变量r1的mcs结果对比；(b)飞行轨迹的mcs结果对比。

图6为稳健优化(ro)结果与确定优化(do)结果性能函数及最优控制曲线对比：(a)质量m变化曲线对比；(b)推力大小||tc||对比。

具体实施方式

下面结合附图并举实施例，对本发明进行详细描述。

本发明提供了一种基于混沌多项式和序列凸优化的飞行器轨迹优化方法，包括如下步骤：

步骤一：构建飞行器轨迹稳健优化数学模型

其中，x为设计变量，u为控制变量，w为随机参数变量，j为目标函数，g为约束函数，k^*为自定义常数，下角标μ和σ分别表示该变量的均值和标准差，nieq为不等式约束的个数，上标lb、ub分别表示对应变量的下限和上限；下标0和f分别表示初始状态和终端状态。

可根据具体问题，在步骤一中采用等式变换、变量代换及无损松弛等方法对方程组(1)进行凸化处理，减少后续工作的工作量。

步骤二：根据广义混沌多项式理论将方程组(1)中的随机微分方程公式(1-b)扩展为由混沌多项式系数构成的高维常微分方程。

1)将每个随机状态变量xi(t)(i＝1,...,n)以及参数变量wk(k＝1,...,s)表示为广义混沌多项式扩展模型(广义pce模型)：

其中，d为不确定性因素的个数，p为混沌多项式的阶次，δ为属于askey方案的标准随机矢量，φ(δ)为正交混沌多项式，下文简写为φ，xij为状态变量xi的第j个未知pce系数；wij为随机参数wi的第j个pce系数，可由wi的随机分布确定。

2)将公式(2)和公式(3)代入公式(1-b)，并在等式两边分别用φi进行galerkin投影，根据正交多项式的性质，得

其中，“<>”表示内积；

可简写为：

其中x与w分别是由状态变量x、随机参数w的pce系数组成的矢量，具体形式如下：

x＝[x10(t),…,x1p(t),x20(t),…,x2p(t),…,xn0(t),…,xnp(t)]^t(6)

w＝[w10,…,w1p,w20,…,w2p,…,ws0,…,wsp]^t(7)

步骤三：基于混沌多项式理论，将原飞行器轨迹稳健优化数学模型转化为等效的确定性最优控制问题。

原飞行器轨迹稳健优化问题可转化为高维确定性最优控制问题，具体形式如下：

步骤四：对确定性动力学微分方程(8-b)进行凸化。

选择一条参考轨迹{xr,ur}，并在此处对方程(8-b)进行一阶泰勒展开，得：

其中，c1＝f(xr,ur,w)-a1xr-b1ur，和分别表示f在参考轨迹处对x和u的偏导数。

步骤五：通过线性微分方程(9)，计算状态x、约束gj、性能函数j的均值及标准差。

根据混沌多项式理论，第i个随机状态变量xi的均值及标准差可分别表示如下：

通常，约束gj、性能函数j由状态变量x的加、减、乘、除、指数、三角函数等基本运算组成。因此，约束gj、性能函数j的pce模型也是状态变量x的pce模型的响应组合。其具体计算形式如下：

1)加减形式c＝xk±xl

pce系数ci可以表示为：

ci＝xki±xli,i＝0,...,p(13)

2)乘积形式c＝xkxl

pce系数ci可以表示为：

3)倒数形式c＝1/xk

则pce系数ci可通过下式求解

4)指数形式

可对其进行泰勒展开，则c可表示为：

其中，nt是泰勒展开阶数。

pce系数ci可通过下式求解

5)正弦函数形式c＝sin(xk)

利用三角函数公式,得:

利用泰勒展开公式，得；

将公式(21)及公式(22)代入公式(20)，可计算得pce系数ci。

其余基本运算与上述几种类似，均利用泰勒展开后，根据公式(14)和公式(15)计算其相应的pce系数。这样，约束gj、性能函数j的pce系数已得到，可根据公式(10)和公式(11)计算其均值及标准差。

步骤六：将高维确定性最优控制问题公式(8)中的非凸约束公式(8-c)及公式(8-e)、非凸性能函数公式(8-a)进行凸化。

1)对于非凸约束公式(8-c)，可在参考轨迹{xr,ur}处对其进行一阶泰勒展开，得：

2)类似的，非凸性能函数公式(8-a)也可以进行泰勒展开，得：

3)对于非凸约束公式(8-e)，由于随机状态变量xi的方差可表示为如下形式：

其中，yi＝[x((i-1)(p+1)+2),x((i-1)(p+1)+3),…,x(i(p+1))]^t，

q为由<φj²(δ)>(j＝1,2,...,p)组成的p维对角矩阵。

由于<φj²(δ)>＞0，所以可对q进行cholesky分解，得：

q＝ll^t(l∈r^p×p)(26)

因此，随机状态变量xi的标准差可表示为

将公式(27)代入公式(8-e)，可将该非凸约束转化为如下两个二阶锥约束：

以上所有公式组成一个二阶锥规划问题p^ed-socp：

步骤七：将二阶锥规划问题p^ed-socp离散

运用梯形法则将确定性微分方程公式(8-b)离散，得：

其中，a(k)＝a1(xr(k),ur(k),w),b(k)＝b1(xr(k),ur(k),w),c(k)＝c1(xr(k),ur(k),w),

t＝(tf-t0)/k，k为总的离散分段数。

性能函数可以离散为

其中jμ(k)＝jμ(xr(k),ur(k),w),jσ(k)＝jσ(xr(k),ur(k),w),

其余约束需要保证在所以离散点处满足。自此，就实现了飞行器轨迹稳健优化的建模过程，该离散问题可通过内点法求解，即可得到最优控制变量，完成飞行器轨迹优化。

下面以航天器在火星着陆的末端——动力下降段的轨迹优化为例，进行说明，该阶段的着陆示意图如图2所示。着陆器视为质点，且不考虑火星大气对航天器的气动影响。在着陆过程中，为保证在着陆器对着陆点的持续跟踪观测，需要满足滑面约束，即保证着陆器与目标点之间连线与地面之间夹角大于4度。着陆器的位置矢量为r＝[r1；r2；r3]，初始位置r(t0)＝[1500；500；2000]m，速度矢量为v＝[v1；v2；v3]，初始速度v(t0)＝[-75；40；100]m/s，初始质量m(t0)＝1905kg，其中初始时刻t0＝0s；终端位置r(tf)＝[0；0；0]m，末端速度v(tf)＝[0；0；0]m/s，末端时刻tf＝81s；此外，整个飞行过程中，发动机推力大小||tc||控制在0.3倍～0.8倍最大推力tmax之间，tmax＝1.3258×10⁴n。根据以上条件，构成一个以消耗燃料最少为目标的确定性轨迹优化问题，如下所示：

上式中，α＝5.09×10-⁴s/m为燃料消耗系数，g＝[-3.7114m/s²,0,0]^t为火星表面重力加速度矢量，tc＝[tc1；tc2；tc3]为推力控制矢量。x0＝[r1(t0),r2(t0),r3(t0),v1(t0),v2(t0),v3(t0),m(t0)]；

高斯伪谱法(gp)是一种常用的轨迹优化方法，本发明将其与序列凸优化(sco)方法进行了对比，如图3所示，由图3结果可见，高斯伪谱法与序列凸优化方法在求解确定性轨迹优化问题时，结果几乎完全一致。

在上述确定性优化问题的基础上，假设初始状态x0＝[r1(t0),r2(t0),r3(t0),v1(t0),v2(t0),v3(t0),m(t0)]及燃料消耗系数α分别服从±2(m,m/s,kg)波动与±1％α波动的均匀分布。则确定性轨迹优化问题转化为稳健轨迹优化问题。然后，按如下步骤，求解上述稳健轨迹优化问题。

1.通过引入松弛变量γ(t)代替||tc||，同时引入新的约束||tc||≤γ(t)，公式(32-d)变为公式(32-j)变为0.3tmax≤γ(t)≤0.8tmax。

2.根据公式(4)对公式(33-b)、公式(33-c)及公式(33-d)进行扩维，将其转化成由pce系数组成的高维确定性微分方程组，其中质量m倒数的pce系数可根据公式(16)计算。确定性不等式约束公式(33-k)两边平方以后，根据公式(12)及公式(14)转化为pce模型，再根据公式(10)及公式(11)计算该不等式约束pce模型的均值和标准差。公式(33-l)可直接变为r1μ(t)-k*r1σ(t)≥0m

3.根据公式(9)及公式(22)对扩维以后的高维确定性微分方程组和不等式约束进行线性化

4.将线性化之后的微分方程组、约束以及性能函数离散，然后用凸优化工具包求解，结果如图4所示；分别对稳健优化(ro)结果及确定性优化(do)结果做蒙特卡罗仿真(mcs)对比，结果如图5所示；稳健优化(ro)结果与确定优化(do)结果性能函数及最优控制曲线对比，结果如图6所示，计算时间如表1所示。

表1计算时间对比

计算时间及设计变量数量对比

由以上结果可知，稳健优化结果能够在初始状态及系统参数不确定的情况下，保证飞行过程中的约束可满足，而确定性优化结果在受到不确定性因素影响时，会违反约束。

对于低维轨迹优化问题，序列凸优化与高斯伪谱法结果几乎一致，而高斯伪谱法计算时间(0.38s)是凸优化方法计算时间(10.52s)的27.68倍。扩维后的高维轨迹优化问题，高斯伪谱法计算时间超过12小时，依然不能求解，而序列凸优化方法仅需要17.18s即可得到正确结果，充分证明该方法有较高的计算效率。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。