一种脱硫塔系统的智能建模及控制方法与流程

本发明涉及脱硫系统技术领域，具体而言，涉及一种脱硫塔系统的智能建模及控制方法。

背景技术：

石灰石/石膏湿法脱硫具有技术成熟、可靠性高、脱硫剂来源广、对煤种适应性强、脱硫产物能够加以利用等众多优点，这一脱硫技术越来越受到现代化电厂的青睐。然而，面对越来越严格的so2排放浓度限值要求，加之石灰石/石膏湿法脱硫反应过程复杂，脱硫效率受众多因素影响，整个脱硫控制系统具有非线性、纯迟延、时变性等特点。原有的脱硫系统手动控制、简单的单回路控制或锅炉负荷前馈控制方法很难满足要求，且控制效果不理想。

技术实现要素：

为解决上述问题，本发明的目的在于提供一种控制精度高和抗干扰能力强的脱硫塔系统控制方法。

本发明提供了一种脱硫塔系统的智能建模及控制方法，该方法包括以下步骤：

步骤101：采用bp神经网络模型对脱硫塔系统进行动态建模，确定bp神经网络模型的输入量和输出量，得到脱硫塔系统智能模型；

步骤102：通过pi控制器调节所述脱硫塔系统智能模型的输入量；

步骤103：确定模糊控制器及模糊规则；

步骤104：通过所述模糊控制器对所述pi控制器的参数进行调节；

步骤105：验证脱硫塔系统智能模型的控制精度。

作为本发明进一步的改进，步骤101中，所述bp神经网络模型的输入量为浆液循环泵转速和喷浆量，所述bp神经网络模型的输出量为出口so2浓度和浆液池ph值；并将现场采集的多组历史数据作为所述bp神经网络模型的输入对模型进行训练。

作为本发明进一步的改进，步骤101中，将现场采集的数据分为两部分，一部分作为训练数据参与所述bp神经网络的训练，另一部分作为验证数据用于验证训练后的所述bp神经网络模型的精度。

作为本发明进一步的改进，步骤103中，所述模糊控制器以误差与误差的微分为输入量，所述模糊控制器的输入量的模糊子集均取为{nb,nm,ns,z0,ps,pm,pb}，所述模糊控制器以pi控制中的参数的变化量作为输出量。

作为本发明进一步的改进，步骤103中，所述输入量和输出量的隶属度函数均采用高斯隶属函数gaussmf与三角隶属函数trimf结合的方式，解模糊方法为重心法。

作为本发明进一步的改进，步骤103中，所述模糊控制器和所述pi控制器的参数kp和ki的初始值相同。

作为本发明进一步的改进，步骤105中，加入阶跃扰动信号，对不同负荷工况分别进行仿真，并将仿真结果与常规pi控制进行比较，验证脱硫塔系统智能模型的抗干扰能力。

本发明的有益效果为：通过采用bp神经网络对脱硫系统的动态特性进行建模，并利用模糊控制器将pi控制器的参数调整到最优状态，实现了快速、精准、鲁棒性强的控制；且在采用bp神经网络对脱硫系统进行动态建模时，没有向神经网络输入当前时刻的浆液循环泵转速和喷浆量，因此可以利用该模型对脱硫系统下一时刻的输出做出预测，并且有较高的精度。

附图说明

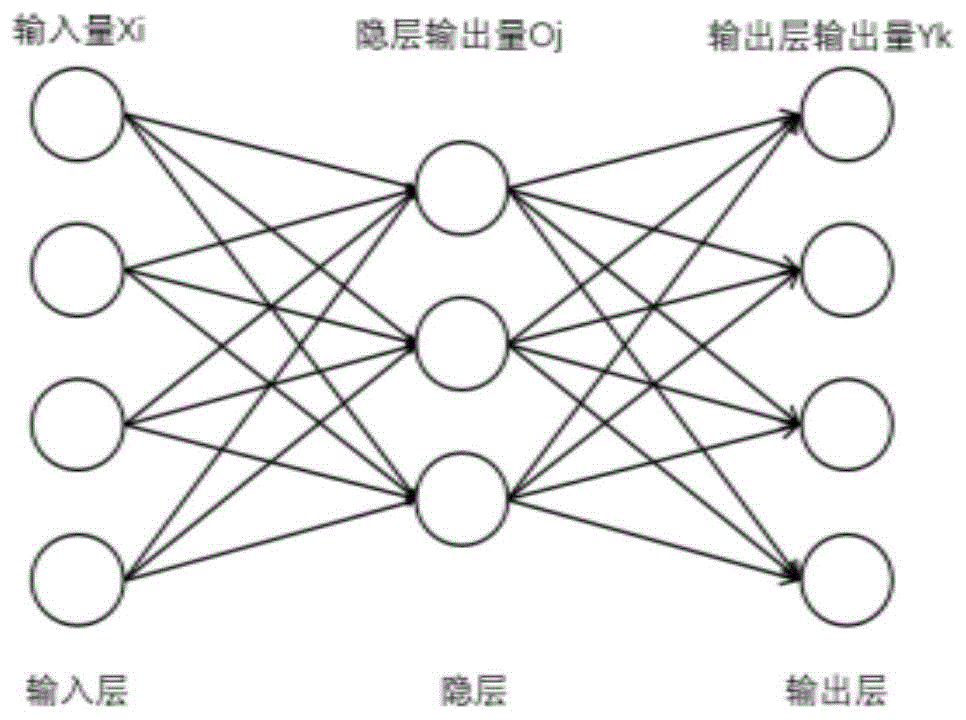
图1为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的神经网络结构示意图；

图2为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的脱硫塔系统智能模型的示意图；

图3为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的bp神经网络的输出量出口so2的输出图；

图4为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的bp神经网络的输出量浆液池ph的输出图；

图5为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的bp神经网络的输出量的训练数据相对误差图；

图6为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的bp神经网络的输出量的验证数据相对误差图；

图7为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的模糊控制的控制逻辑图；

图8为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的模糊控制的电路结构示意图；

图9为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的常规pi控制的电路结构示意图；

图10为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的pi控制的隶属函数图；

图11为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的阶跃响应图；

图12为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的阶跃响应图；

图13为本发明实施例所述的一种脱硫塔系统的智能建模及控制方法的流程图。

具体实施方式

下面通过具体的实施例并结合附图对本发明做进一步的详细描述。

如图1-2所示，本发明实施例所述的一种脱硫塔系统的智能建模及控制方法，该方法包括以下步骤：

步骤101：采用bp神经网络模型对脱硫塔系统进行动态建模，确定bp神经网络模型的输入量和输出量，得到脱硫塔系统智能模型；

步骤102：通过pi控制器调节所述脱硫塔系统智能模型的输入量；

步骤103：确定模糊控制器及模糊规则；

步骤104：通过所述模糊控制器对所述pi控制器的参数进行调节；

步骤105：验证脱硫塔系统智能模型的控制精度。

本发明使用bp神经网络建模，bp网络模型处理信息的基本原理是：输入信号xi通过中间节点(隐层点)作用于输出节点，经过非线形变换，产生输出信号yk，网络训练的每个样本包括输入向量xi和期望输出量t，网络输出值y与期望输出值t之间的偏差，通过调整输入节点与隐层节点的联接强度取值wij、隐层节点与输出节点之间的联接强度tjk以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止，其结构模型如图1所示。经过训练的神经网络能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

为提高模型精度，如图7-9所示，利用模糊控制器对pi控制器的参数进行调节，再利用该pi控制器调节浆液循环泵转速和喷浆量。具体实现方式为：模糊控制器以误差e为输入量1，以误差e的导数ec为输入量2，依据模糊规则输出pi控制中的参数kp的变化量dkp和参数ki的变化量dki，对kp和ki进行微调，每次微调后的kp和ki分别记为kpn和kin。参数kp和ki在控制中的作用为：

比例系数kp：使控制系统快速动作，减小系统误差。kp较大时，系统能快速响应，但kp过大时会产生超调，甚至破坏系统的稳定性；kp过小时，会减弱控制器动作幅度，调节时间增长，使系统响应不理想。

积分系数ki：系统进入稳态阶段时会消除系统误差。ki较大时，系统稳态误差会很快变小，但在系统初始响应阶段ki较大时，会使控制器产生积分饱和，从而破坏系统的稳定性；ki过小时，难以消除系统的稳态误差，不能确保较高的调节精度。

进一步的，步骤101中，所述bp神经网络模型的输入量为浆液循环泵转速和喷浆量，所述bp神经网络模型的输出量为出口so2浓度和浆液池ph值；并将现场采集的多组历史数据作为所述bp神经网络模型的输入对模型进行训练。烟气脱硫的方法是湿法石灰石-石膏烟气脱硫法，整个脱硫系统的控制方式具有非线性、纯迟延、时变性的特点。输入系统的脱硫浆液的ph值一般需要控制在5.5左右，ph值与浆液循环泵的转速和喷浆量有关；采用bp神经网络对脱硫系统的动态特性进行建模，主要关注脱硫系统的浆液循环泵转速、喷浆量、出口so2浓度、浆液池ph值。

进一步的，步骤101中，将现场采集的数据分为两部分，一部分作为训练数据参与所述bp神经网络的训练，另一部分作为验证数据用于验证训练后的所述bp神经网络模型的精度。

本实施例中将三门峡电厂脱硫系统中采集到的数据分为两部分：一部分用于训练神经网络，称为训练数据；一部分不参与训练，而用于神经网络的验证，这部分数据称为验证数据。将训练好的神经网络运用在验证数据中，可以得到，应用本模型得到的输出与电厂采集数据中的实际输出十分接近，误差可以被控制在2％以内，如图3-6所示。

进一步的，步骤103中，所述模糊控制器以误差与误差的微分为输入量，所述模糊控制器的输入量的模糊子集均取为{nb,nm,ns,z0,ps,pm,pb}，其中n代表negative(负向)，p代表positive(正向)，b代表big(大)、m代表midium(中)、s代表small(小)，所述模糊控制器以pi控制中的参数的变化量作为输出量。模糊规则根据表1设计。

表1

针对脱硫控制系统的非线性，采用了模糊pi控制。本发明选用传递函数作为被控对象，应用模糊控制器，同时使用常规pi控制系统作为对比，分别对两种控制并进行阶跃响应测试。以误差e为输入量1，以误差e的微分ec为输入量2，以pi控制中的kp的变化量dkp和ki的变化量dki分别作为输出量1和输出量2。模糊规则一般根据经验确定，依据图7进行设计。

进一步的，步骤103中，pi控制器输入量和输出量的隶属度函数均采用高斯隶属函数gaussmf与三角隶属函数trimf结合的方式，解模糊方法为重心法。隶属函数图如图10所示。

进一步的，步骤103中，所述模糊控制器和所述pi控制器的参数kp和ki的初始值相同。

进一步的，步骤105中，加入阶跃扰动信号，对不同负荷工况分别进行仿真，并将仿真结果与常规pi控制进行比较，验证系统的抗干扰能力。由于脱硫控制系统的传递函数具有时变性，因此对模糊pi控制系统和常规pi控制系统进行了摄动实验，即在一定范围内改变被控对象的传递函数，多次测试其阶跃响应。图11和图12是两张阶跃响应图，在t＝500s时加入一个阶跃扰动信号，对不同负荷工况分别进行仿真，并将仿真结果与常规pi控制进行比较；通过对比可知，模糊pi控制系统阶跃响应曲线的超调量约为常规pi控制系统阶跃响应曲线超调量的1/5，抗干扰能力也有较大提升，鲁棒性强。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。