一种渐变芯厚立铣刀容屑槽法截面的建模方法与流程
本发明属于渐变芯厚立铣刀容屑槽设计领域,特别是一种渐变芯厚立铣刀容屑槽法截面的建模方法。
背景技术:
立铣刀因其良好的材料去除率、加工表面质量以及复杂三维曲面加工能力,在现代铣削加工中得到广泛应用。容屑槽是立铣刀的关键结构之一,在加工中具有容屑、排屑作用,为增加刀具排屑能力,通常加大容屑槽深度,即减小芯厚。然而,芯厚的减小将减弱刀具刚性,导致加工过程中产生刀具挠性变形、加工颤振等问题。为平衡容屑能力与刀具刚性之间的矛盾关系,具有渐变芯厚容屑槽的立铣刀应运而生,渐变芯厚容屑槽指刀具芯厚由靠近刀尖位置向靠近刀柄位置方向逐渐增加,在提高容屑槽能力的同时,保证刀具具有良好的刚性。立铣刀周刃法截面形状是刀具切削性能的重要影响因素之一,然而,由于渐变芯厚容屑槽为空间复杂螺旋曲面,现有技术获取渐变芯厚容屑槽法截面形状较为困难,成为制约渐变芯厚立铣刀研制的瓶颈技术之一。
孙杰,李国超,李剑峰在文献“一种基于刃磨过程的整体式立铣刀容屑槽建模方法”提出了一种基于刃磨过程的整体式立铣刀容屑槽建模方法,用于整体式立铣刀制造过程中容屑槽模型的求解,基于刃磨过程的建模方法可以真实的反应容屑槽的实际加工结果。但该方法以不变芯厚容屑槽为研究对象,且仅求得容屑槽端截面模型,无法进行渐变芯厚容屑槽法截面建模。
在背景技术部分中公开的上述信息仅仅用于增强对本发明背景的理解,因此可能包含不构成在本国中本领域普通技术人员公知的现有技术的信息。
技术实现要素:
针对现有技术中存在的问题,本发明提出一种渐变芯厚立铣刀容屑槽法截面的建模方法。
本发明的目的是通过以下技术方案予以实现。
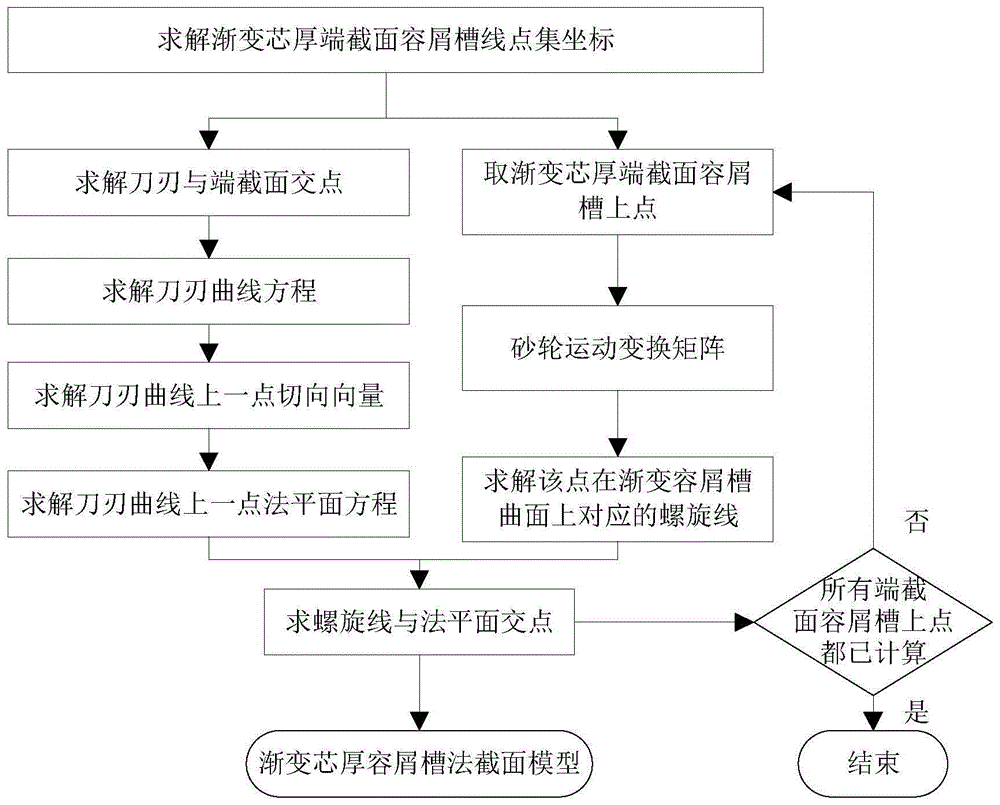
一种渐变芯厚立铣刀容屑槽法截面的建模方法包括以下步骤:
第一步骤中,砂轮为回转体,建立砂轮坐标系xwywzw-ow,坐标平面xwowyw与回转体的第一端平面重合,坐标轴zw与砂轮轴线重合且指向第二端平面,坐标轴xw、yw与zw组成笛卡尔坐标系,砂轮回转轮廓在砂轮坐标系xwywzw-ow中的参数方程:
wrq(m1,m2)=[wxq,wyq,wzq,1]t=[rg_m1·cos(m2),rg_m1·sin(m2),m1,1]t,
其中,wrq指砂轮回转轮廓上任意一点在砂轮坐标系中的坐标向量,下标q指砂轮回转面上任一点,上标w指在砂轮坐标系中取值,wxq、wyq和wzq分别指点q与砂轮坐标系中的坐标轴xw、yw与zw之间的距离,ml为砂轮回转面上任一点与坐标平面xwowyw之间的距离,m2为砂轮回转面上任一点在坐标平面xwowyw上的投影和坐标原点ow的连线与坐标轴xw之间的夹角,rg_ml为与坐标平面xwowyw之间的距离为ml处砂轮回转半径;
第二步骤中,建立渐变芯厚容屑槽的加工,其中,砂轮坐标系相对毛坯坐标系从重合位置到初始加工位置的变换矩阵m:
其中,立铣刀毛坯为圆柱体,立铣刀毛坯坐标系xtytzt-ot中的坐标平面xtotyt与圆柱体其中一个端面重合,坐标轴zt与所述圆柱体轴线重合,并指向另一个端面,坐标轴xt、yt与zt组成笛卡尔坐标系,δαx为初始时刻砂轮轴线与毛坯轴线之间的夹角,δx、δy、δz分别为砂轮坐标系原点与毛坯坐标系中的坐标轴xt、yt与zt之间的距离;
第三步骤中,建立任意时刻砂轮回转轮廓在立铣刀毛坯坐标系xtytzt-ot中的参数方程:
其中,上标t指在毛坯坐标系中取值,txq、tyq和tzq分别指点q与毛坯坐标系中的坐标轴xt、yt与zt之间的距离,t为加工过程中砂轮绕毛坯轴线旋转角度,p为渐变芯厚容屑槽导程,且θ为渐变芯厚容屑槽芯部与毛坯轴线形成的锥角,
第四步骤中,获得渐变容屑槽在坐标平面xtotyt上的点,记为pci,构成端截面点集,其中,i指该点在点集中的序号,该点在毛坯坐标系中的坐标值表示为(xpci,ypci,zpci),并且pc0指刀刃曲线与渐变芯厚容屑槽端截面之间的交点;
第五步骤中,建立渐变芯厚容屑槽法截面模型,法截面为过立铣刀刃上一点k且于刀刃曲线在k点处的切线相垂直的平面,渐变芯厚容屑槽法截面模型为所述平面截取渐变芯厚容屑槽获得的平面曲线模型,其中,
s5-1,建立点pci在渐变芯厚容屑槽曲线上对应的螺旋线表达式:
s5-2,建立刀刃曲线在k点处切向量表达式:
其中,
s5-3,求解点pci在渐变芯厚容屑槽曲线上对应的螺旋线与过立铣刀刃上一点k且于刀刃曲线在k点处的切线相垂直的平面之间的交点,求解方程
s5-4,求解与渐变芯厚容屑槽端截面点pci对应的,在k点处的渐变芯厚容屑槽法截面上点的坐标,将求解t值代入点pci在渐变芯厚容屑槽曲线上对应的螺旋线表达式;
s5-5,重复s5-1至s5-4,使得所有渐变芯厚容屑槽端截面线上点都求解获得对应的法截面上点,以获得渐变芯厚容屑槽在点k处的法截面模型。
所述的方法中,第一步骤中,砂轮为双锥面形砂轮。
所述的方法中,第四步骤中,离散化以获得渐变容屑槽在坐标平面xtotyt上的点。
根据所述建模方法对刀具结构进行优化的方法,根据所述法截面模型预测刀具性能,进而优化刀具结构。
有益效果
本发明提出的方法可在刀具实际加工之前预测渐变芯厚容屑槽法截面形状,为刀具设计及制造提供参考,可有效提高刀具研制效率,降低研制成本,精实际验证,该方法有效、可靠。
上述说明仅是本发明技术方案的概述,为了能够使得本发明的技术手段更加清楚明白,达到本领域技术人员可依照说明书的内容予以实施的程度,并且为了能够让本发明的上述和其它目的、特征和优点能够更明显易懂,下面以本发明的具体实施方式进行举例说明。
附图说明
通过阅读下文优选的具体实施方式中的详细描述,本发明各种其他的优点和益处对于本领域普通技术人员将变得清楚明了。说明书附图仅用于示出优选实施方式的目的,而并不认为是对本发明的限制。显而易见地,下面描述的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。而且在整个附图中,用相同的附图标记表示相同的部件。
在附图中:
图1是根据本发明一个实施例的渐变芯厚立铣刀容屑槽法截面的建模方法的步骤示意图;
图2是根据本发明一个实施例的渐变芯厚立铣刀容屑槽法截面的建模方法的变芯厚容屑槽立铣刀示意图;
图3是根据本发明一个实施例的渐变芯厚立铣刀容屑槽法截面的建模方法的变芯厚容屑槽法截面模型示意图;
以下结合附图和实施例对本发明作进一步的解释。
具体实施方式
下面将参照附图1至图3更详细地描述本发明的具体实施例。虽然附图中显示了本发明的具体实施例,然而应当理解,可以以各种形式实现本发明而不应被这里阐述的实施例所限制。相反,提供这些实施例是为了能够更透彻地理解本发明,并且能够将本发明的范围完整的传达给本领域的技术人员。
需要说明的是,在说明书及权利要求当中使用了某些词汇来指称特定组件。本领域技术人员应可以理解,技术人员可能会用不同名词来称呼同一个组件。本说明书及权利要求并不以名词的差异来作为区分组件的方式,而是以组件在功能上的差异来作为区分的准则。如在通篇说明书及权利要求当中所提及的“包含”或“包括”为一开放式用语,故应解释成“包含但不限定于”。说明书后续描述为实施本发明的较佳实施方式,然所述描述乃以说明书的一般原则为目的,并非用以限定本发明的范围。本发明的保护范围当视所附权利要求所界定者为准。
为便于对本发明实施例的理解,下面将结合附图以具体实施例为例做进一步的解释说明,且各个附图并不构成对本发明实施例的限定。
为了更好地理解,图1为基于刚度变化的铣削颤振抑制方法的建模过程示意图,如图1所示,一种渐变芯厚立铣刀容屑槽法截面的建模方法包括以下步骤:
第一步骤s1中,砂轮为回转体,建立砂轮坐标系xwywzw-ow,坐标平面xwowyw与回转体的第一端平面重合,坐标轴zw与砂轮轴线重合且指向第二端平面,坐标轴xw、yw与zw组成笛卡尔坐标系,砂轮回转轮廓在砂轮坐标系xwywzw-ow中的参数方程:
wrq(m1,m2)=[wxq,wyq,wzq,1]t=[rg_ml·cos(m2),rg_ml·sin(m2),m1,1]t,
其中,下标q指砂轮回转面上任一点,上标w指在砂轮坐标系中取值,wxq、wyq和wzq分别指点q与砂轮坐标系中的坐标轴xw、yw与zw之间的距离,ml为砂轮回转面上任一点与坐标平面xwowyw之间的距离,m2为砂轮回转面上任一点在坐标平面xwowyw上的投影和坐标原点ow的连线与坐标轴xw之间的夹角,rg_ml为与坐标平面xwowyw之间的距离为ml处砂轮回转半径;
第二步骤s2中,建立渐变芯厚容屑槽的加工,其中,砂轮坐标系相对毛坯坐标系从重合位置到初始加工位置的变换矩阵m:
其中,立铣刀毛坯为圆柱体,立铣刀毛坯坐标系xtytzt-ot中的坐标平面xtotyt与圆柱体其中一个端面重合,坐标轴zt与所述圆柱体轴线重合,并指向另一个端面,坐标轴xt、yt与zt组成笛卡尔坐标系,δαx为初始时刻砂轮轴线与毛坯轴线之间的夹角,δx、δy、δz分别为砂轮坐标系原点与毛坯坐标系中的坐标轴xt、yt与zt之间的距离;
第三步骤s3中,建立任意时刻砂轮回转轮廓在立铣刀毛坯坐标系xtytzt-ot中的参数方程:
其中,上标t指在毛坯坐标系中取值,txq、tyq和tzq分别指点q与毛坯坐标系中的坐标轴xt、yt与zt之间的距离,t为加工过程中砂轮绕毛坯轴线旋转角度,p为渐变芯厚容屑槽导程,且θ为渐变芯厚容屑槽芯部与毛坯轴线形成的锥角,
第四步骤s4中,获得渐变容屑槽在坐标平面xtotyt上的点,记为pci,构成端截面点集,其中,i指该点在点集中的序号,该点在毛坯坐标系中的坐标值表示为(xpci,ypci,zpci),并且pc0指刀刃曲线与渐变芯厚容屑槽端截面之间的交点;
第五步骤s5中,建立渐变芯厚容屑槽法截面模型,法截面为过立铣刀刃上一点k且于刀刃曲线在k点处的切线相垂直的平面,渐变芯厚容屑槽法截面模型为所述平面截取渐变芯厚容屑槽获得的平面曲线模型,其中,
s5-1,建立点pci在渐变芯厚容屑槽曲线上对应的螺旋线表达式:
s5-2,建立刀刃曲线在k点处切向量表达式:
其中,
s5-3,求解点pci在渐变芯厚容屑槽曲线上对应的螺旋线与过立铣刀刃上一点k且于刀刃曲线在k点处的切线相垂直的平面之间的交点,求解方程
s5-4,求解与渐变芯厚容屑槽端截面点pci对应的,在k点处的渐变芯厚容屑槽法截面上点的坐标,将求解t值代入点pci在渐变芯厚容屑槽曲线上对应的螺旋线表达式;
s5-5,重复s5-1至s5-4,使得所有渐变芯厚容屑槽端截面线上点都求解获得对应的法截面上点,以获得渐变芯厚容屑槽在点k处的法截面模型。
渐变芯厚容屑槽的立铣刀具有良好的刚性,在高性能铣削加工中得到广泛应用,渐变芯厚容屑槽法截面形状包含立铣刀周刃法向前角,直接决定刀具切削性能,然而现有方法难以准确获得渐变芯厚容屑槽法截面形状。本发明在获得渐变芯厚容屑槽端截面模型的基础上,通过渐变芯厚立铣刀容屑槽法截面建模,得到了精确的渐变芯厚容屑槽法截面形状,显著提高了刀具的切削性能,在渐变芯厚立铣刀设计及制造领域具有广泛的应用前景。
所述的方法的一个实施例中,第一步骤s1中,砂轮为双锥面形砂轮。
所述的方法的另一个实施例中,第四步骤s4中,离散化以获得渐变容屑槽在坐标平面xtotyt上的点。
在一个实施例中,提供一种根据所述方法对刀具结构进行优化的方法,根据所述法截面模型预测刀具性能,进而优化刀具结构。
在该实施例中,将建模方法中建立的法截面模型具体应用于预测刀具性能,进而优化刀具结构,可实现有效提高刀具研制效率,降低研制成本的目的。
为了进一步理解本发明,下面结合具体实例描述本发明:
本实施实例以刃磨直径为20mm,导程为62.8mm,渐变容屑槽芯部与毛坯轴线形成的锥角θ=0.17见图2的变芯厚容屑槽立铣刀为例,选用双锥面形砂轮,砂轮直径为150mm,厚度为20mm,砂轮两个锥角分别为70°和10°,70°锥角对应的砂轮厚度为15mm,砂轮回转轮廓过渡处圆角为1mm,初始时刻砂轮轴线与毛坯轴线之间的夹角δαx为0.72,为砂轮坐标系原点与毛坯坐标系中的坐标轴xt、yt与zt之间的距离δx、δy、δz分别77mm、0mm、-30mm。变芯厚容屑槽法截面建模过程如图1所示。
步骤1:建立砂轮回转轮廓在砂轮坐标系xwywzw-ow中的参数方程:
wrq(m1,m2)=[wxq,wyq,wzq,1]t=[rg_m1·cos(m2),rg_m1·sin(m2),m1,1]t
步骤2:建立变芯厚容屑槽加工,砂轮坐标系相对毛坯坐标系从重合位置到初始加工位置的变换矩阵m:
步骤3:建立任意时刻砂轮回转轮廓在立铣刀毛坯坐标系xtytzt-ot中的参数方程:
步骤4:采用文献1“孙杰,李国超,李剑峰,等.一种基于刃磨过程的整体式立铣刀容屑槽建模方法:,cn103777568a[p].2014.”所述方法,获得渐变容屑槽在坐标平面xtotyt上的点pci,其中pc0=(-6.48,7.35,0);
步骤5:建立渐变芯厚容屑槽法截面模型,该法截面指过立铣刀刃上一点k且于刀刃曲线在k点处的切线相垂直的平面,设点k处t取值为1.04,此时点k
在毛坯坐标系中的坐标值为(-9.34,-1.40,10.40),
①建立点pci在渐变芯厚容屑槽曲线上对应的螺旋线表达式:
②建立刀刃曲线在k点处切向量表达式:
其中,
③求解点pc1=(-6.16,6.51,0)在渐变芯厚容屑槽曲线上对应的螺旋线与过立铣刀刃上一点k且于刀刃曲线在k点处的切线相垂直的平面之间的交点,求解方程1.23·cos(t)-1.69·t-0.828·sin(t)-0.0142·t·cos(t)+0.0854·t·sin(t)+1.74=0,可得t=1.026;
④求解与渐变芯厚容屑槽端截面点pcl对应的,在k点处的渐变芯厚容屑槽法截面上点的坐标为(-8.48,-1.43,10.26);
⑤重复过程①、②、③、④至所有变芯厚容屑槽端截面线上点都求解获得对应的法截面上点,获得渐变芯厚容屑槽在点k处的法截面模型,见图3。
尽管以上结合附图对本发明的实施方案进行了描述,但本发明并不局限于上述的具体实施方案和应用领域,上述的具体实施方案仅仅是示意性的、指导性的,而不是限制性的。本领域的普通技术人员在本说明书的启示下和在不脱离本发明权利要求所保护的范围的情况下,还可以做出很多种的形式,这些均属于本发明保护之列。
- 还没有人留言评论。精彩留言会获得点赞!