一种电驱动四足机器人的控制系统的制作方法

本发明涉及一种用于电驱动四足机器人的控制系统，属于电驱动四足机器人控制技术领域。

背景技术：

腿足式机器人一直是移动机器人比较热门的研究领域，腿足式机器人在动态稳定性和复杂地形适应性方面都胜过轮式机器人。电驱动机器人作为腿足式机器人的一个热门分支更是具有以上优越的特点。电驱动机器人是指采用力矩电机作为驱动关节运动的关键单元的机器人，其中又分为直驱方式、准直驱方式和sea方式。

直驱方式的电驱动机器人直接将电机的输出轴与关节连杆相连，这种驱动方式控制效果最好，但是对力矩电机的要求比较高，目前的力矩电机纯输出力矩还达不到高力矩性能，而且性能越高意味着成本越高。sea方式是指在力矩电机和连杆之间加弹簧装置，利用弹簧的储能特性来减轻对力矩电机的性能高要求，但是这种方式动力学模型复杂，实际控制效果很难达到理想状态。准直驱方式是指在电机和连杆之间加一级减速器的方案，这样既能达到直驱的控制效果，也能放大电机的输出力矩。

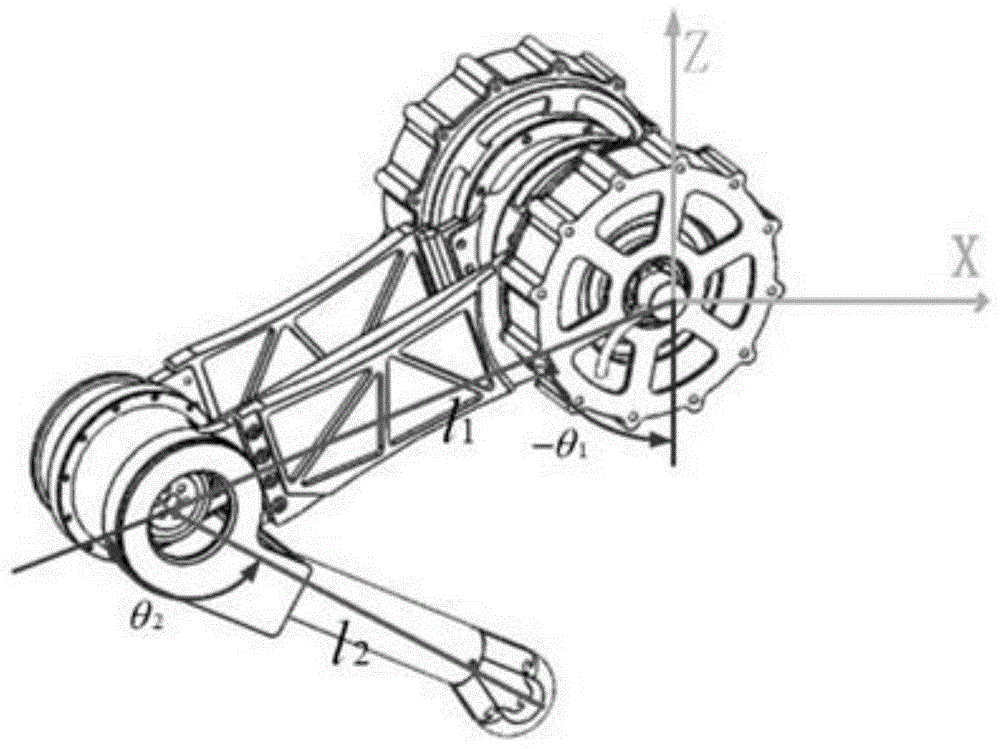
电驱动四足机器人二自由度准直驱方式的单腿结构(本发明中所用)如图1所示，包括大腿关节4、大腿连杆5、小腿关节6和小腿连杆7。电驱动四足机器人整体仿真模型结构如图2所示，包括躯干1和四条三自由度的单腿，躯干1通过髋关节2连接髋部连杆3，胯部连杆3、大腿关节4、大腿连杆5、小腿关节6和小腿连杆7依次连接，小腿连杆7的底部设置足底传感器8。足底传感器8用来检测机器人单腿足端是否触地的关键部件。大腿关节4和小腿关节6都是由力矩电机和减速器组成，减速器为一级行星减速器，电机通过一级行星减速器带动大腿关节4或小腿关节6转动。单腿的相应的正运动学和逆运动学可以得出。正运动学为的是通过编码器传输上来的电机角度来得出整个单腿足端位于图1所示坐标系中的位置。下面进行具体分析。

根据图1所示的基座标系以及各关节连杆参数，可推导出足端相对于基座的正运动学方程如下：

已知单腿足端位置，可反解求得二自由度单腿的关节角：

对二自由度单腿求导，可得单腿的雅可比矩阵：

以上各式中所求的角度θ1，θ2为图1中对应的大腿关节4和小腿关节6的关节角，x，z为足端在基座标中的位置。l1、l2分别为大腿连杆5和小腿连杆7的长度。l12为图1中足端到基坐标系原点的直线距离。

在四足机器人领域，实时性的控制系统搭建一直是四足机器人领域比较核心的问题。当前有很多实时性系统方案，如美国麻省理工学院的cheetah2用的是ni公司提供的控制器以rs-422通信为基础搭建的实时系统，瑞士苏黎世联邦理工学院的starleth采用的是基于ros机器人系统的实时性系统等，或是采用公司的成熟方案，或是基于机器人系统搭建。但是由于采用的都不是专业的实时性系统，当前的电动腿足式机器人的实时性系统性能表现一般，仍然有提升的方面。

在机器人领域，提升机器人的能量利用效率一直是一个亟需解决的问题。这个问题具体到电驱动机器人主要集中在足端触地过程中的能量优化、足端轨迹和四足步态的选择。

技术实现要素：

本发明针对现有的电驱动四足机器人在实时性和高效性控制方面存在的问题，提供一种准确可行、实时性高的电驱动四足机器人的控制系统。

本发明的电驱动四足机器人的控制系统，包括大腿关节和小腿关节，大腿关节和小腿关节都是由电机和减速器连接而成，该控制系统采用以下技术方案：

该控制系统，包括上位机、工控机、驱动器和编码器，工控机与上位机连接进行传输数据，工控机和编码器均与驱动器连接；编码器固定在关节电机的输出端，用于检测关节电机旋转的角度，通过编码器测得的脉冲数和关节减速器的减速比得到关节的旋转角度，编码器将脉冲数上传至驱动器，驱动器再将经过滤波的脉冲值上传至工控机，然后工控机运行，得出机器人各关节的输出力矩并转换成电流值传递给驱动器，驱动器通过内置的电流环实现电机输出给定的力矩，实现对单腿的柔性优化和碰撞能量优化。

上位机实现人与机器人的交互界面。在机器人运动过程中，可以通过上位机给机器人发控制指令，例如，前进、跳跃等。

所述工控机运行控制算法实现对单腿的柔性优化和碰撞能量优化，该控制算法，包括单腿触地碰撞过程优化以及四足运行轨迹和步态优化；单腿触地碰撞是一个连续的动力学求解过程，利用将连续线性问题转化为随机线性问题并结合高斯分布求得参数结果，优化后的参数表达式如下：

上式是基本的拉格朗日动力学公式，其中，m(q)为拉格朗日质量矩阵，为质量加速度，τ为输出力矩，fg为合外力，结合高斯分布求得最后的表达式：

e[min(h，bg)²]＝h²-σ²(h+b)f(h)+(σ²+b²-h²)f(h)

其中的e表示期望值，h，bg都是标量参数，σ用来描述这一过程的参数的平均值分布和离散程度；f(h)由下式求得：

其中，f(t)为期望函数，表示误差函数，

以上便得到触地碰撞能量损失结果；

通过对伯恩斯坦多项式的运用求出足端轨迹，表达式如下：

其中p1(t)，p2(t)，p3(t)为轨迹曲线的三部分分段规划的相对于基座标系的x，z坐标,t表示当前系统的时间；a0～a14表示规划的足端曲线的预设点的相对于基座标系的x，z坐标；

通过结合触地碰撞优化和足端轨迹曲线得出飞驰对角步态，两条对角的单腿触地而另两条对角的单腿腾空。

所述工控机与上位机通过tcp/ip协议进行传输数据，所述工控机与驱动器通过can总线连接。所述编码器通过信号线与驱动器连接。

所述机器人关节的旋转角度θ的计算公式为ni为编码器检测到的脉冲数，de为机器人关节减速器的减速比。

本发明通过控制算法的改进减少了单腿触地的能量损失，提升了硬件系统的整体实时性和可靠性以及四足机器人的高速运动，控制算法主要实现四足机器人的高速运动，仿真的结果表示本发明的控制算法可以使四足机器人达到18km/h的平均速度，并且能够保持良好的动态稳定性和高能量效率。

附图说明

图1是现有电驱动四足机器人的单腿结构运动学建模示意图。

图2是现有所用的电驱动四足机器人的仿真模型示意图。

图3是本发明中控制系统的结构原理示意图。

图4是本发明中控制算法规划的轨迹示意图。

图5是飞驰对角(flying-trot)步态示意图。

图中：1.躯干，2.胯关节，3.胯部连杆，4.大腿关节，5.大腿连杆，6.小腿关节，7.小腿连杆，8.足底传感器。

具体实施方式

本发明的用于电驱动四足机器人的控制系统是针对图1所示二自由度单腿结构，如图3，该控制系统，包括上位机、工控机、驱动器和编码器，工控机与上位机通过tcp/ip协议进行传输数据，工控机与驱动器通过can总线连接，编码器通过专用信号线与驱动器连接，编码器固定在电机输出端。编码器用于检测电机旋转的角度，通过编码器测得的脉冲数和已知的图1中小腿关节处的一级行星减速器的减速比de就可以得到图1所示的腿足式机器人的大腿和小腿关节的旋转角度，编码器将脉冲数上传至驱动器，驱动器再将经过滤波的脉冲值通过图3所示的can通讯总线上传至工控机实现数据采集的全过程，然后工控机运行本发明中的控制算法，得出需要腿足式机器人各关节的输出力矩，转换成电流值，通过can通信传递给驱动器，驱动器通过内置的电流环实现电机输出给定的力矩。

工控机采用德国控创公司的keex-5000系列的工控机并通过pcie插槽扩展peak公司的can卡实现工控机与驱动器之间的can通信，由12v直流电池单独对工控机以及散热风扇供电，另由格氏提供的24v电池串联达到48v作为单腿的直流总电源。工控机带有电源指示灯和can通信指示灯。如图3所示，工控机与单腿的大腿关节4和小腿关节6的两个驱动器之间通过can总线连接，并通过can的高层协议canopen协议实现数据编码传输以及解析。工控机运行的系统是由黑莓公司的qnx实时系统，qnx系统具有高实时性和可靠性的特点，特别适合机器人领域。通过其特有的qnxmomentic软件编译本发明中的控制算法代码可实现对单腿的柔性优化和碰撞能量优化。

编码器采用雷尼绍型号为rmb20ic13bc10的相对式编码器，精度为8192，即电机每转一圈，编码器将采集到8192个脉冲，该型编码器精度高，体积小，非常适合电机角度的检测。通过编码器检测到的脉冲数，利用公式：可以得到关节的旋转角度θ1，θ2，ni为编码器检测到的脉冲数，de为一级行星减速器的减速比。然后本发明中的控制算法调用正运动学计算出足端相对于基坐标系的位置以及通过已知的控制频率计算出瞬时速度。

上述系统在实际单腿运动中表现出良好的实时性能和高可靠性能。

本发明中的控制算法包括单腿触地碰撞过程优化以及四足运行轨迹和步态优化(单腿的跳跃运动、四足机器人的flying-trot步态运动)。

单腿触地碰撞是一个连续的动力学求解过程，但是现实环境中获得的输入参数不足以支持求出能够接受的结果。所以利用将连续线性问题转化为随机线性问题并结合高斯分布，可以求得一个较为精确的参数结果。优化后的参数表达式如下：

上式是基本的拉格朗日动力学公式，其中，m(q)为拉格朗日质量矩阵，为质量加速度，τ为输出力矩，fg为合外力，结合高斯分布，可求得最后的表达式：

e[min(h，bg)²]＝h²-σ²(h+b)f(h)+(σ²+b²-h²)f(h)

其中的e表示期望值，h，bg都是标量参数，σ用来描述这一过程的参数的平均值分布和离散程度。f(h)由下式求得：

其中，f(t)为期望函数，表示误差函数。以上便可以得到一个较小的触地碰撞能量损失结果。

如图4，通过对伯恩斯坦多项式的运用可以求出一个较优的足端轨迹，轨迹表达式如下：

其中p1(t)，p2(t)，p3(t)为轨迹曲线的三部分分段规划的相对于基座标系的x，z坐标,t表示当前系统的时间。a0～a14表示规划的足端曲线的预设点的相对于基座标系的x，z坐标。

如图5，步态通过结合触地碰撞优化和轨迹曲线得出一种“飞驰对角“步态，也就是两条对角的单腿触地，而另两条对角的单腿腾空。图5中的黑色圆圈表示对应的三自由度单腿触地，白色圆圈代表对应的三自由度单腿腾空。整图表示的是一个周期四足机器人的单腿触地变化。

以上便是具体的控制算法的全部。这个算法主要实现四足机器人的高速运动，仿真的结果表示上述本发明的控制算法可以使四足机器人达到18km/h的平均速度，并且能够保持良好的动态稳定性和高能量效率。