一种判断多回路控制系统裕度的方法与流程

本发明涉及一种判断多回路控制系统裕度的方法。

背景技术：

基于经典控制系统设计而言，需对开环控制回路的频率指标进行测试，即计算开环控制回路的相位和幅值裕度及截止频率等，进而对控制回路的控制品质进行评定。但是对于多回路控制系统设计和分析，控制理论以及工程实例均表明：存在相位和幅值裕度及截止频率均满足设计指标，控制品质和鲁棒性表现不佳的情况，说明仅依据相位和幅值裕度去判断多回路控制系统的控制品质和鲁棒性的方法是有局限的。

技术实现要素：

本发明的技术解决问题是：克服现有技术的不足，本发明提出一种判断多回路控制系统裕度的方法，此控制系统裕度定义为延迟裕度，可视为多回路控制系统的绝对稳定裕度，适用于多回路控制系统设计和分析。

本发明的技术解决方案是：一种判断多回路控制系统裕度的方法，包括以下步骤：

步骤1、对多回路控制系统进行等价变换，变换为一个非单位反馈的单回路控制系统；

多回路控制系统由内回路和外回路构成，内回路控制为反馈控制器gc2(s)，外回路控制为前向通路控制器gc1(s)；

单回路控制系统的前向通道回路传递函数g(s)为

g(s)＝gc1(s)s(s)p1(s)p2(s)；

其中，s(s)为执行机构，p1(s)为被控对象，p2(s)为前向通路其它控制环节；

单回路控制系统的反馈回路传递函数h(s)可表示为

步骤2、计算得到变换后的开环回路传递函数open(s)：

步骤3、根据开环回路传递函数open(s)计算得到截止频率为相位裕度为在此基础上计算延迟裕度dm：

根据dm判断多回路控制系统的控制裕度。

本发明与现有技术相比具有的有益效果是：

(1)基于控制理论及工程实例，具有充裕相位和幅值裕度的多回路控制系统存在控制品质和鲁棒性不佳的情况，引入的延迟裕度概念可以精确地衡量控制系统的控制品质和鲁棒性；

(2)本发明的方法计算获得的控制系统延迟裕度物理意义明确，仅需对多回路控制系统进行等价变换后即可求解得到，易于在控制回路设计中应用，设计者可以根据此值对控制回路的绝对裕度进行判定。

(3)通过本发明的方法计算获得控制系统延迟裕度，相对于相位裕度和幅值裕度而言，更能说明多回路控制系统的控制品质和鲁棒性，对于多回路控制系统具有通用性，可视为多回路控制系统的绝对稳定裕度，适用于多回路控制系统设计和分析。

附图说明

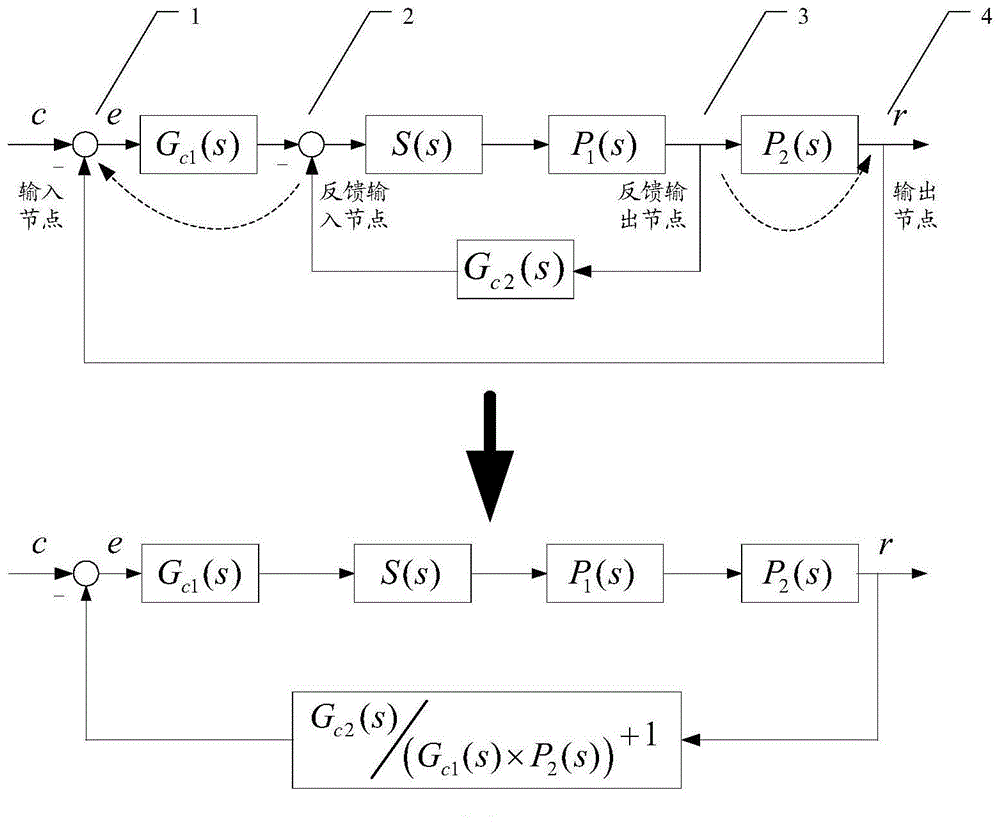
图1为多回路控制系统等价变换过程；

图2为原开环回路对应两组不同控制参数时的bode图；

图3为变换后开环回路对应两组不同控制参数时的bode图；

图4为两组不同控制参数在执行机构未加入和加入延迟环节时的单位阶跃响应。

具体实施方式

本发明提供一种判断多回路控制系统裕度的方法，此控制系统裕度定义为延迟裕度，可定量计算得到多回路控制系统的延迟裕度，进而判定控制系统的控制品质以及鲁棒性，可用于多回路控制系统设计及分析，包括以下步骤：

步骤1、对图1所示的多回路控制系统进行等价变换，即将内回路的反馈输出节点3移至系统的输出节点4，将内回路的反馈输入节点2移至系统的输入节点1，即变换为一个非单位反馈的单回路控制系统，其前向通道回路传递函数为

g(s)＝gc1(s)s(s)p1(s)p2(s)

反馈回路传递函数可表示为

其中，gc1(s)为前向通路控制器，s(s)为执行机构，p1(s)为被控对象，p2(s)为前向通路其它控制环节，gc2(s)为内回路的反馈控制器；

多回路控制系统由内回路和外回路构成，内回路控制为反馈控制gc2(s)，外回路控制为前向通路控制器gc1(s)；

步骤2、根据经典控制理论，变换后非单位反馈单回路控制系统的开环回路传递函数为

步骤3、根据开环回路传递函数open(s)计算得到截止频率为相位裕度为则延迟裕度dm定义如下

与控制系统相位与幅值裕度不同，延迟裕度的物理意义可理解为控制信号在执行机构处滞后延迟裕度时，系统临界稳定。在工程应用上，延迟裕度可视为控制系统的绝对裕度，当其值较大时，则表征控制系统具有较充裕的裕度，反之亦然。

所述的前向通道回路传递函数，即从回路的输入节点1到系统的输出节点4所包含的各个环节组合而成的传递函数，变换后的开环回路与原开环回路在前向通道传递函数上保持一致。

所述的反馈回路传递函数，即从回路的输出节点4到系统输入节点1所包含的各个环节，属于外回路负反馈，负反馈于回路的输入节点1与指令形成的控制误差量。

所述的变换后的开环回路传递函数，由前向通道回路传递函数与反馈回路传递函数乘积得到。

计算机仿真实施例：

某多回路控制系统控制框图如图1所示，执行机构传函为被控对象为传函内回路反馈控制系数为gc2(s)＝kd，前向串联比例控制为gc(s)＝kp，两组控制参数分别为sys1：kd＝0.9，kp＝4.0；控制参数sys2：kd＝2.9，kp＝12.0。

按经典控制理论，可得控制系统的开环传函为

系统sys1和sys2开环bode如图2所示，可求解得到sys1和sys2的频域指标，sys1：ωc＝4.06rad/s，gm＝14.0db，pm＝76.9°；sys2：ωc＝4.04rad/s，gm＝14.8db，pm＝85.7°。依据系统的相位和幅值裕度去判断控制系统的控制品质，可得出结论：sys1和sys2的控制品质相当。

按本发明介绍方法进行等价变换，可得开环传函为

将sys1和sys2控制参数代入上式，求解得到系统sys1和sys2的bode图如图3所示，当控制参数由sys1变化至sys2时，变换后控制系统的开环截止频率由14.9rad/s增加至31.4rad/s，相位裕度由44.3°减少至28.6°，经求解延迟裕度dm由51.8ms减少至15.9ms，即控制系统sys2的延迟裕度大幅低于系统sys1。

考核系统sys1和sys2的时域特性，分执行机构处无延迟和执行机构处增加15.9ms的延迟环节两种情况仿真sys1和sys2的单位阶跃响应，如图4所示(左图：执行机构处无延迟，右图：执行机构处延迟15.9ms)，由图可知，在执行机构处增加15.9ms的延迟，发现sys2为临界稳定，而sys1具有较大的控制裕度。

仿真结果说明：

(1)即使两个系统控制回路结构和被控对象一样，且具有相近的截止频率、幅值裕度和相位裕度，其控制品质也可能存在很大的差别；

(2)对于多回路控制系统来说，仅依据控制系统的截止频率、相位和幅值裕度去判断控制系统的控制品质和鲁棒性是存在局限性的；

(3)延迟裕度较大的系统对应着较好的控制品质；

(4)等价变换后开环回路的截止频率并不能代表控制系统的快速性，截止频率较高者往往对应着较低的延迟裕度，即控制系统的裕度较小。

本发明未详细说明部分属本领域技术人员公知常识。